Содержание
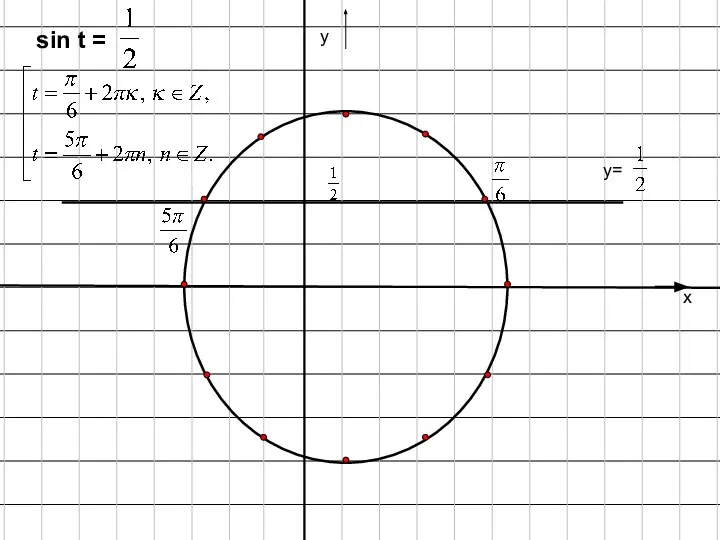
- 2. Решить уравнение: sin t = .
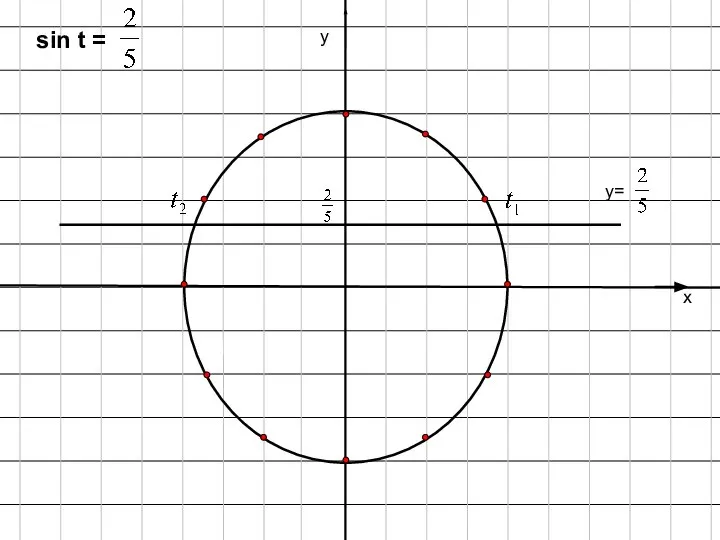
- 3. х у у= sin t =
- 4. х у у= sin t =
- 5. arcsin t Читается: арксинус t «arcus» в переводе с латинского значит «дуга» (сравните со словом «арка»)
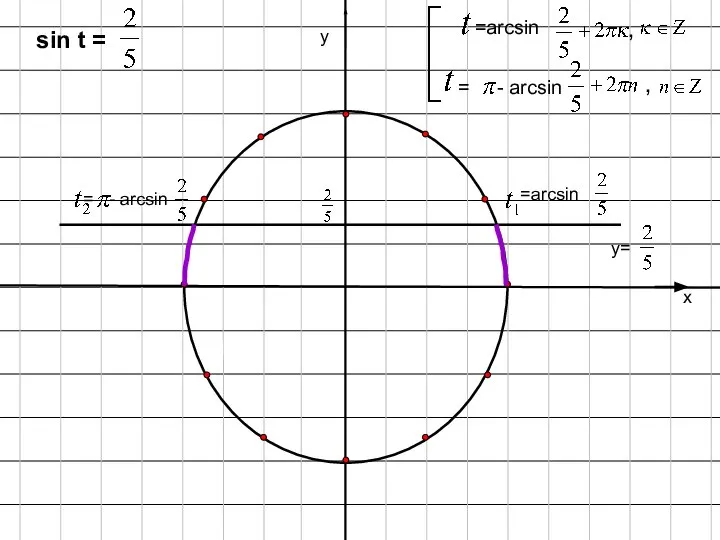
- 6. х у у= sin t = = arcsin = - arcsin , =arcsin , = -
- 7. Что же такое ? arcsin Это – число (длина дуги), синус которого равен и которое принадлежит
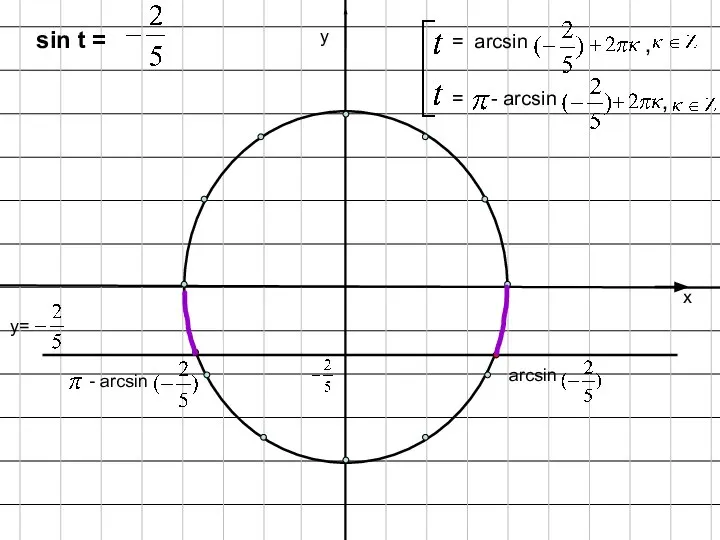
- 8. х у y= sin t = , arcsin - arcsin = arcsin , = - arcsin
- 9. Что же такое ? arcsin Это – число (длина дуги), синус которого равен и которое принадлежит
- 10. Определение. Если IaI
- 11. Пример 1 arcsin = t =?
- 12. Пример 2 arcsin = t =?
- 13. Пример 3 arcsin 0 = t =?
- 14. Для любого а [-1;1] выполняется равенство arcsin a + arcsin (-a) = 0 Теорема. а -а
- 15. arcsin (-a) = - arcsin a , где На практике используется: Пример. arcsin = - arcsin
- 16. Решение уравнения sint = a. Если IaI , то уравнение sint = a имеет две серии
- 17. Решение уравнения sint = a. Если IaI , то уравнение sint = a имеет две серии
- 18. Частные случаи: 1) Если sin t = 0, то t = , 2) Если sin t
- 19. Решение уравнений Пример 1. sin t = Ответ: { }
- 20. Пример 2. sin t = Ответ:
- 21. Решение уравнений Пример 3. sin t = Ответ:
- 22. Решение уравнений Пример 4. sin t = Ответ: уравнение решения не имеет. - 1
- 23. Домашнее задание: §34 № 586, 589, 590, 591
- 25. Скачать презентацию








![Для любого а [-1;1] выполняется равенство arcsin a + arcsin (-a) = 0 Теорема. а -а](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1096209/slide-13.jpg)









 Математическая конференция 6а класса
Математическая конференция 6а класса Сложение и вычитание векторов
Сложение и вычитание векторов Образование дробей. 5 класс
Образование дробей. 5 класс Геометрия (8 класс)
Геометрия (8 класс) Логарифм. Логарифм числа. Основное логарифмическое тождество. Свойства логарифмов
Логарифм. Логарифм числа. Основное логарифмическое тождество. Свойства логарифмов Параллельный перенос
Параллельный перенос Решаем примеры
Решаем примеры Диференціальні рівняння
Диференціальні рівняння Первообразная. Интеграл
Первообразная. Интеграл Геометрический смысл производной f '(x₀) = tg α = к
Геометрический смысл производной f '(x₀) = tg α = к Тетраэдр
Тетраэдр Урок – творческий проект по математике Мастерская игрушек
Урок – творческий проект по математике Мастерская игрушек Подобие треугольников. Применение подобия к решению задач
Подобие треугольников. Применение подобия к решению задач Угол
Угол Равенство и неравенство. (1 класс)
Равенство и неравенство. (1 класс) Тренажёр по математике 4 класс. Умножение и деление многозначных чисел на однозначное
Тренажёр по математике 4 класс. Умножение и деление многозначных чисел на однозначное Математика. Классная работа
Математика. Классная работа Синтез автоматов без памяти
Синтез автоматов без памяти Общее понятие меры
Общее понятие меры Перемещение, путь, траектория. 9 класс
Перемещение, путь, траектория. 9 класс Правильная пирамида
Правильная пирамида Простые и составные числа
Простые и составные числа Вероятность распределения случайных чисел
Вероятность распределения случайных чисел Пересекающиеся прямые
Пересекающиеся прямые Уравнения и неравенства с двумя переменными
Уравнения и неравенства с двумя переменными Арктангенс и арккотангенс
Арктангенс и арккотангенс Объем конуса
Объем конуса