Содержание
- 2. Вопросы: 1. Определение смежных углов и их свойство. 2. Определение вертикальных углов и их свойство. 3.
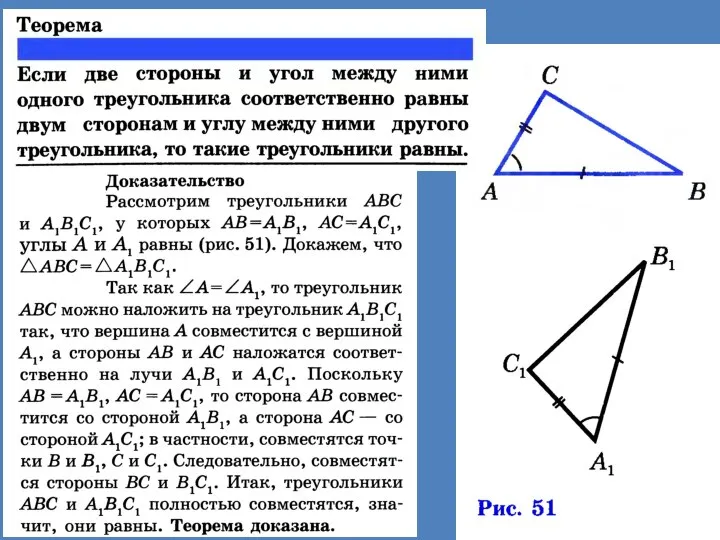
- 3. В геометрии каждое утверждение, справедливость которого устанавливается путем рассуждений, называется теоремой, а сами рассуждения называются доказательством
- 4. Какие фигуры называются равными?
- 5. Два треугольника называются равными, если каждой стороне и каждому углу в любом из них найдется равный
- 7. Доказанная теорема выражает признак (равенство у треугольников двух сторон и угла между ними), по которому можно
- 8. Доказанный признак дает возможность устанавливать равенство двух треугольников, не производя фактического наложения одного из них на
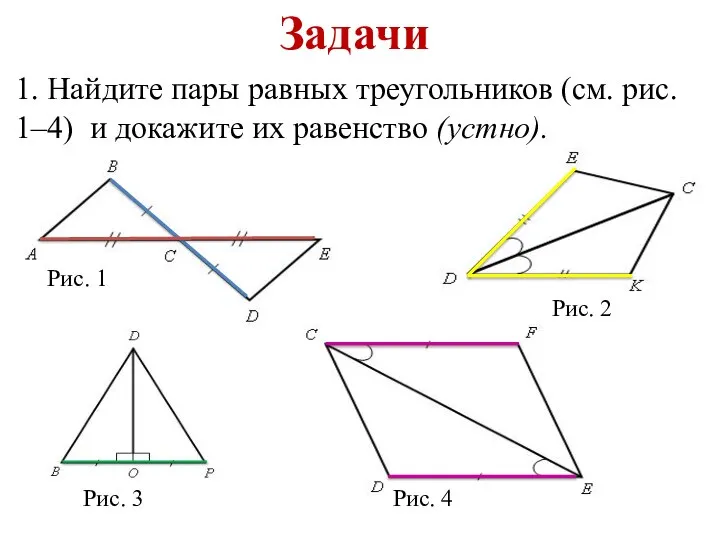
- 9. Задачи 1. Найдите пары равных треугольников (см. рис. 1–4) и докажите их равенство (устно). Рис. 1
- 10. 2. Решить задачу № 96 на доске и в тетрадях (по рис. 54).
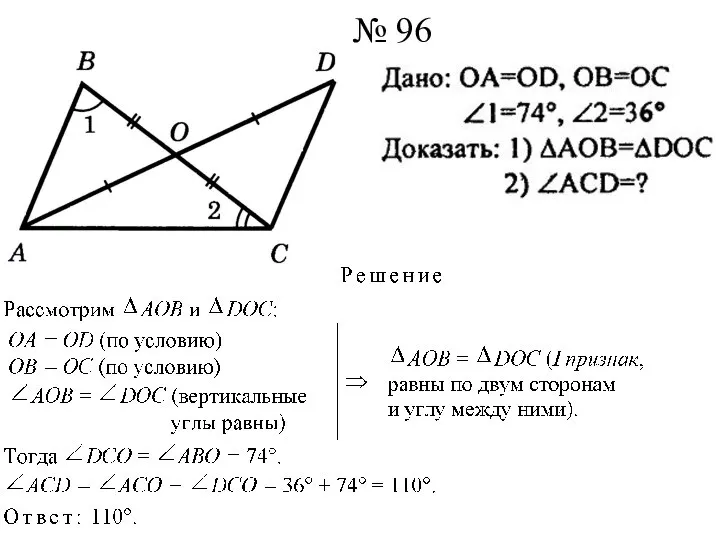
- 11. № 96
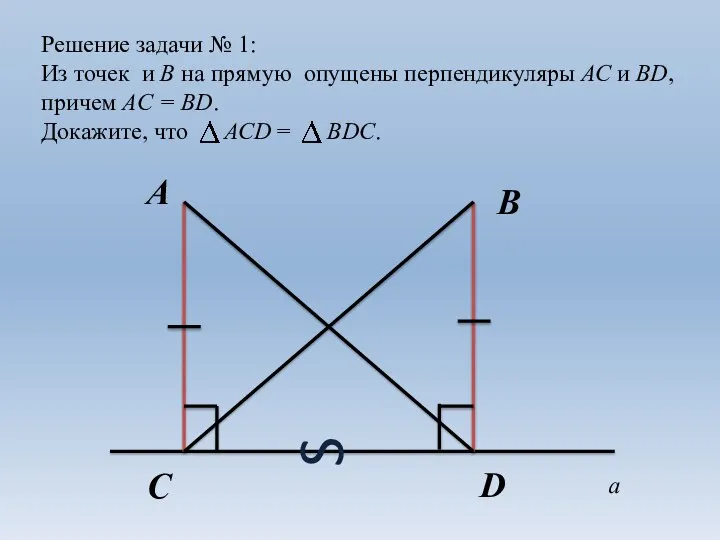
- 12. 3. Самостоятельно решить задачу № 1: Из точек А и В на прямую а опущены перпендикуляры
- 13. Решение задачи № 1: Из точек и В на прямую опущены перпендикуляры АС и ВD, причем
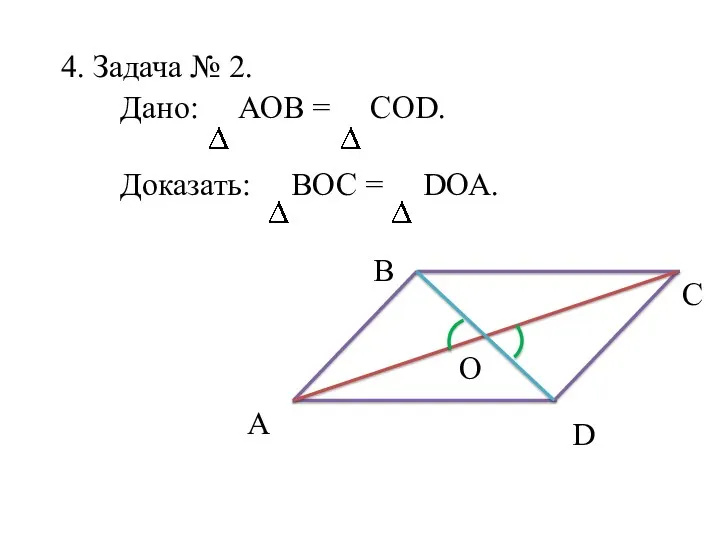
- 14. 4. Задача № 2. Дано: АОВ = СОD. Доказать: ВОС = DОА. А C B O
- 16. Скачать презентацию








 Урок повторения
Урок повторения Презентация на тему Группировка слагаемых. Скобки (1 класс)
Презентация на тему Группировка слагаемых. Скобки (1 класс)  Правила вычисления производных
Правила вычисления производных Трапеция. Свойство углов равнобедренной трапеции
Трапеция. Свойство углов равнобедренной трапеции Математическое описание случайных явлений
Математическое описание случайных явлений Логарифмические уравнения и неравенства
Логарифмические уравнения и неравенства Отображение. Отражение относительно прямой. Преобразование единичного квадрата
Отображение. Отражение относительно прямой. Преобразование единичного квадрата Площадь фигур. Решение задач
Площадь фигур. Решение задач Логарифмы вокруг нас
Логарифмы вокруг нас Производная функции. Часть 1
Производная функции. Часть 1 Состав числа 5
Состав числа 5 Решение задач
Решение задач Решение задач
Решение задач Основные понятия математической статистики. Лекция 6
Основные понятия математической статистики. Лекция 6 Презентация на тему Построение графиков функций, содержащих модуль
Презентация на тему Построение графиков функций, содержащих модуль  Алгоритмы и исполнители
Алгоритмы и исполнители Пифагор и музыка
Пифагор и музыка Планиметрия малыми порциями
Планиметрия малыми порциями Презентация на тему Квадратные корни. Арифметический квадратный корень
Презентация на тему Квадратные корни. Арифметический квадратный корень  Интерактивная игра Геометрические фигуры
Интерактивная игра Геометрические фигуры Решение задач с помощью систем уравнений (часть 2)
Решение задач с помощью систем уравнений (часть 2) Решение задач с помощью уравнений. Урок математики в 5 классе
Решение задач с помощью уравнений. Урок математики в 5 классе Числовые неравенства
Числовые неравенства Простейшие задачи в координатах
Простейшие задачи в координатах Задачи на нахождение неизвестного третьего слагаемого
Задачи на нахождение неизвестного третьего слагаемого Таблица умножения на 3
Таблица умножения на 3 Умножение дробей
Умножение дробей Построение проекции поверхности ликвидуса системы Fe-As-S
Построение проекции поверхности ликвидуса системы Fe-As-S