Содержание
- 2. Цель: Исследование - свойств платоновых тел - роли «Платоновых тел» в различных областях науки и живописи.
- 3. При изучении теории правильных многогранников открывается не только удивительный мир геометрических тел, обладающих неповторимыми свойствами, но
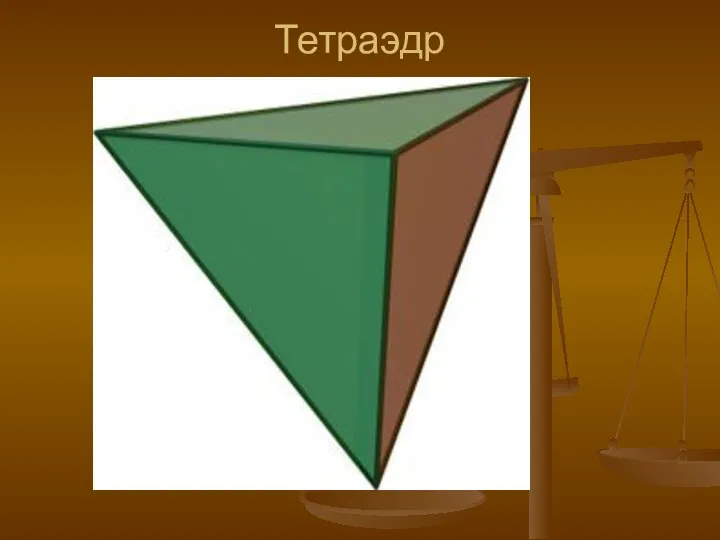
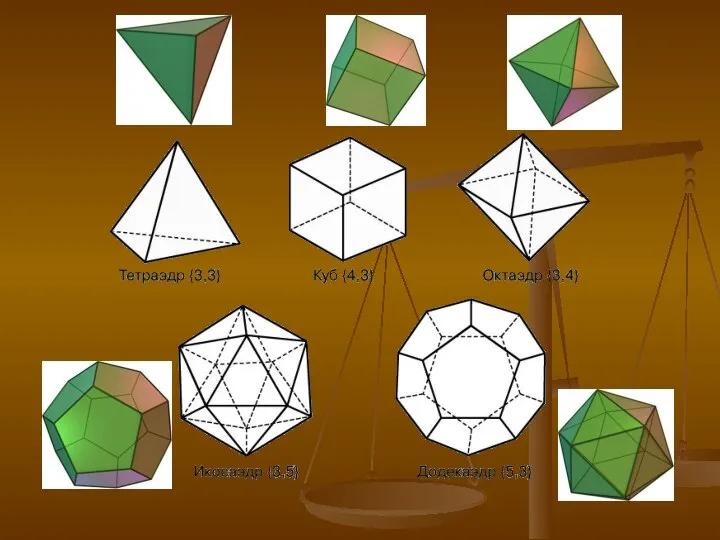
- 4. Тетраэдр
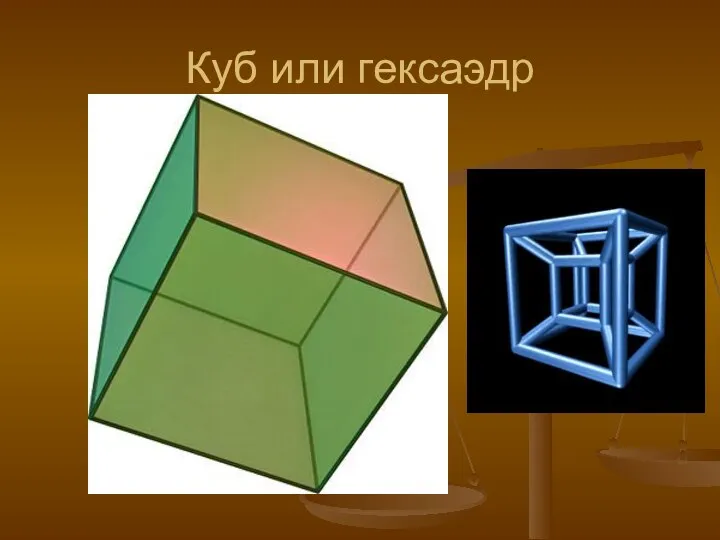
- 5. Куб или гексаэдр
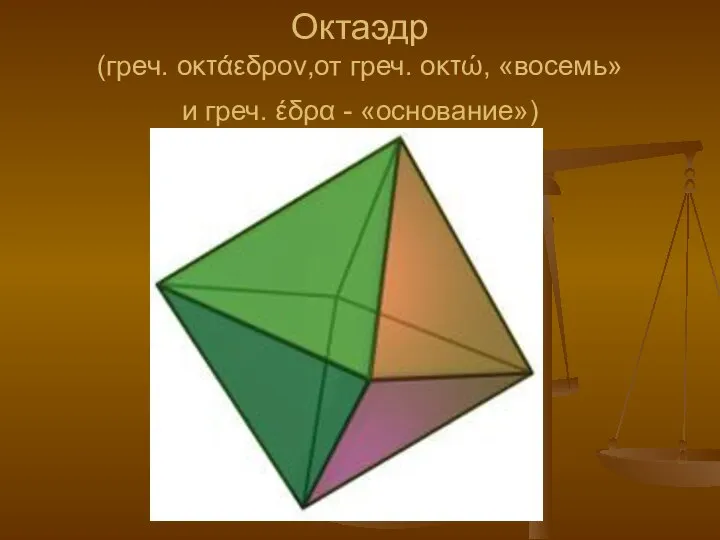
- 6. Октаэдр (греч. οκτάεδρον,от греч. οκτώ, «восемь» и греч. έδρα - «основание»)
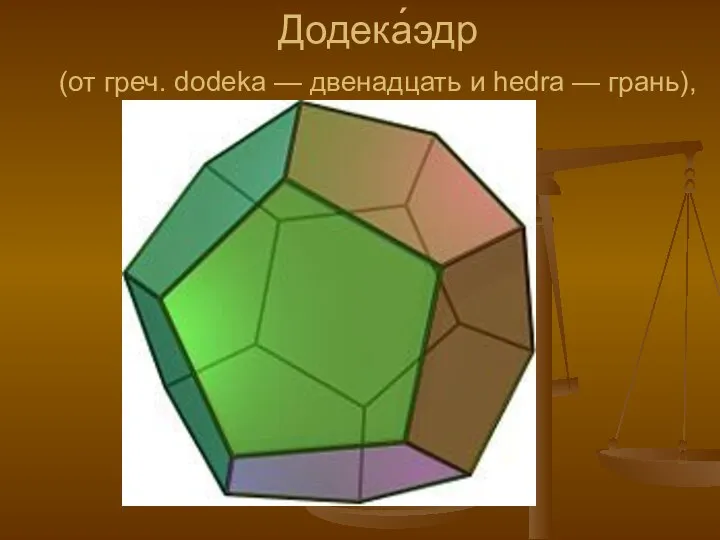
- 7. Додека́эдр (от греч. dodeka — двенадцать и hedra — грань),
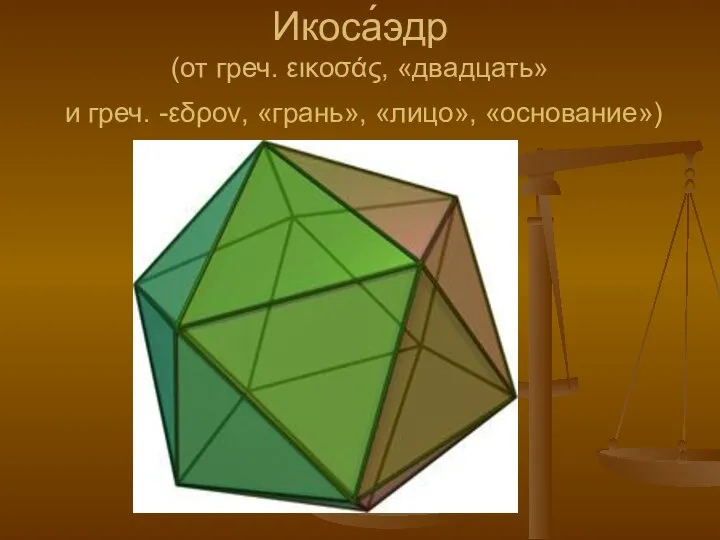
- 8. Икоса́эдр (от греч. εικοσάς, «двадцать» и греч. -εδρον, «грань», «лицо», «основание»)
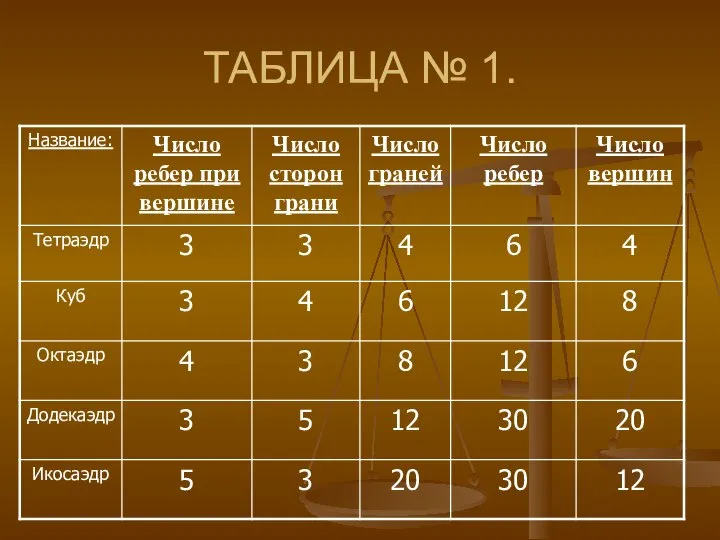
- 10. ТАБЛИЦА № 1.
- 11. ТАБЛИЦА № 2.
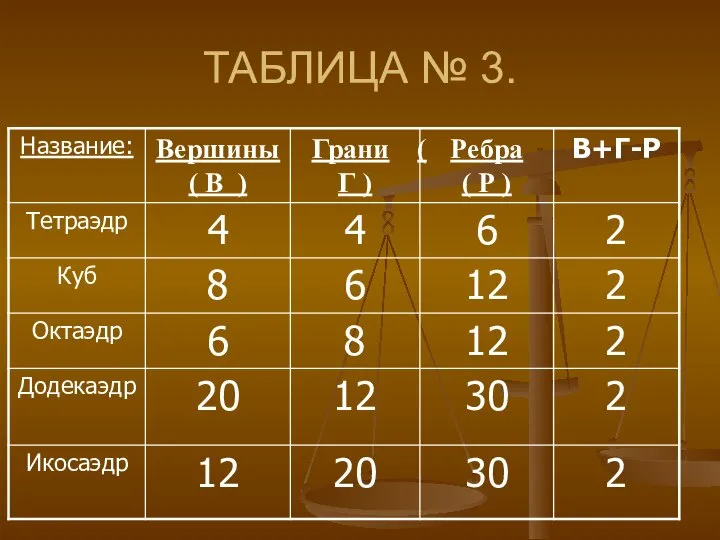
- 12. ТАБЛИЦА № 3.
- 13. Теорема Эйлера Для любого выпуклого многогранника справедливо соотношение Г+В-Р=2, где Г – число граней, В –
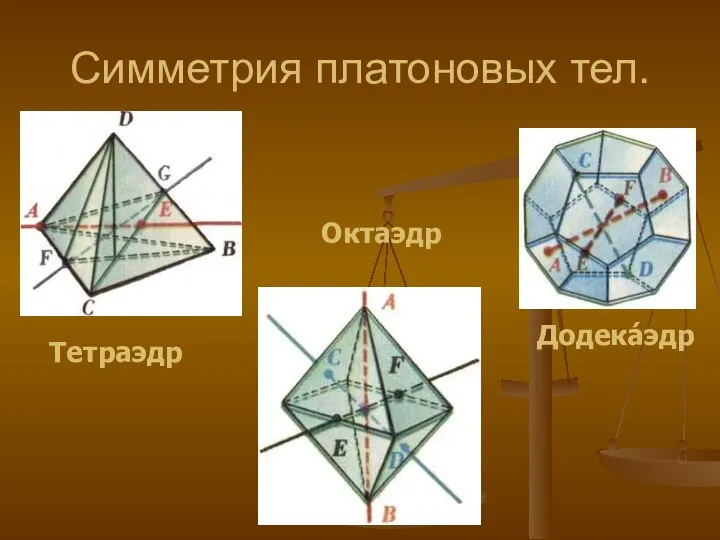
- 14. Симметрия платоновых тел. Тетраэдр Октаэдр Додека́эдр
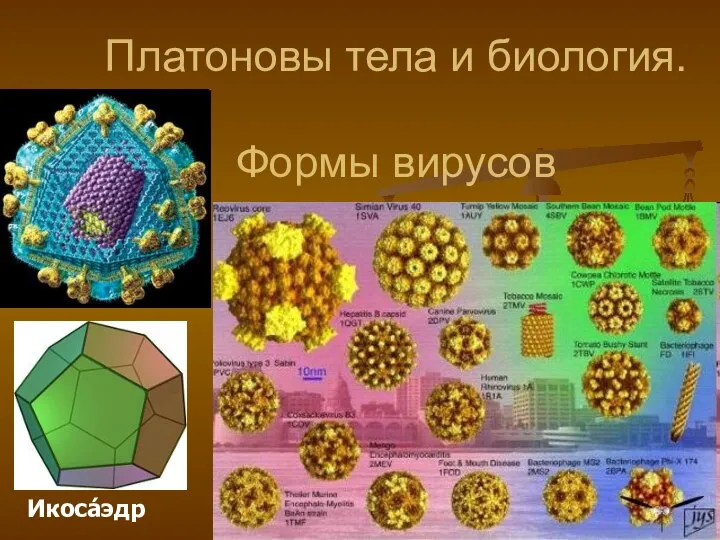
- 15. Платоновы тела и биология. Формы вирусов Икоса́эдр
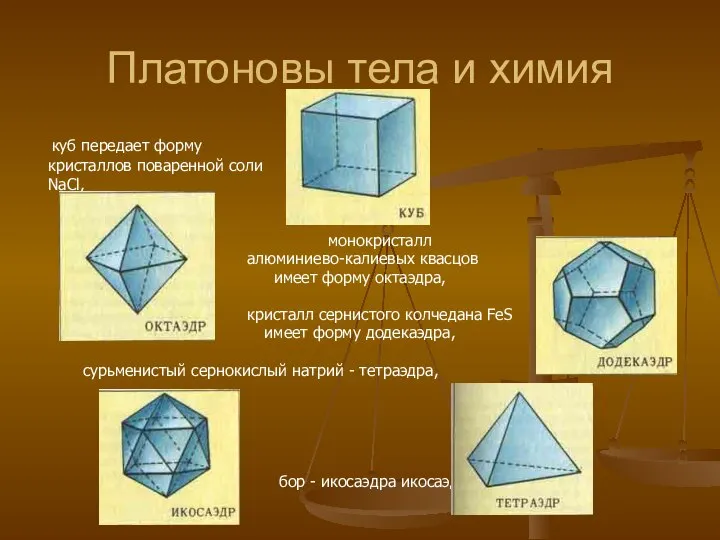
- 16. Платоновы тела и химия куб передает форму кристаллов поваренной соли NaCl, монокристалл алюминиево-калиевых квасцов имеет форму
- 17. Исследование земли
- 18. Архимедовы тела. Архимедовыми телами называются полуправильные , однородные выпуклые многогранники , то есть выпуклые многогранники ,
- 19. Архимедовы тела. . . Конструирование Архимедовых тел (а) усеченный тетраэдр, (б) усеченный куб, (в) усеченный октаэдр,
- 20. Правильные звездчатые многогранники Кеплер первым начал изучать так называемые звездчатые многогранники, которые в отличие от Платоновых
- 21. Платоновы тела и современность. Израильский физик Дан Шехтман М.Т. Крашек на своей выставке ‘Kaleidoscopic Fragrances’, Любляна,
- 24. ЗАКЛЮЧЕНИЕ. Теория многогранников ( платоновых тел) - одна из увлекательных и ярких разделов математики. В идеалистической
- 26. Скачать презентацию












 Случайность. Массовые явления
Случайность. Массовые явления Неопределенность измерения. Порядок расчета
Неопределенность измерения. Порядок расчета Сумма углов треугольника. Работа с чертежами
Сумма углов треугольника. Работа с чертежами Площадь параллелограмма
Площадь параллелограмма Подобные слагаемые. 7 класс
Подобные слагаемые. 7 класс Теоремы синусов и косинусов. Тест
Теоремы синусов и косинусов. Тест Практическая работа
Практическая работа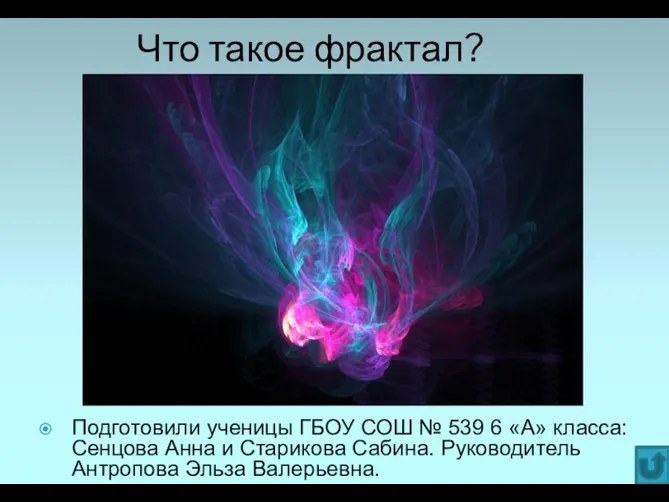 Что такое фрактал?
Что такое фрактал? Путешествие по реке Математическая. Игра
Путешествие по реке Математическая. Игра Начала теории вероятностей
Начала теории вероятностей радианная мера углов
радианная мера углов Построение графика функции
Построение графика функции Комплексные числа
Комплексные числа Построение угла, равного данному
Построение угла, равного данному Презентация на тему ОТЫСКАНИЕ ЧАСТИ ОТ ЦЕЛОГО И ЦЕЛОГО ПО ЕГО ЧАСТИ
Презентация на тему ОТЫСКАНИЕ ЧАСТИ ОТ ЦЕЛОГО И ЦЕЛОГО ПО ЕГО ЧАСТИ  Ответы к тестам для подготовки к ЕГЭ по математике
Ответы к тестам для подготовки к ЕГЭ по математике Презентация на тему Интегральное исчисление
Презентация на тему Интегральное исчисление  Регрессионный анализ
Регрессионный анализ Сумма углов треугольника
Сумма углов треугольника Применение производной в географии. 10 класса
Применение производной в географии. 10 класса Учебный проект Чудесные дроби. 6 класс
Учебный проект Чудесные дроби. 6 класс Неопределенный интеграл
Неопределенный интеграл Габриэль Крамер
Габриэль Крамер Признак перпендикулярности двух плоскостей
Признак перпендикулярности двух плоскостей Перспективная модель ЕГЭ по математике
Перспективная модель ЕГЭ по математике Решение уравнения в 1 классе
Решение уравнения в 1 классе Решение задач с помощью систем уравнений
Решение задач с помощью систем уравнений Самостоятельная работа
Самостоятельная работа