Содержание
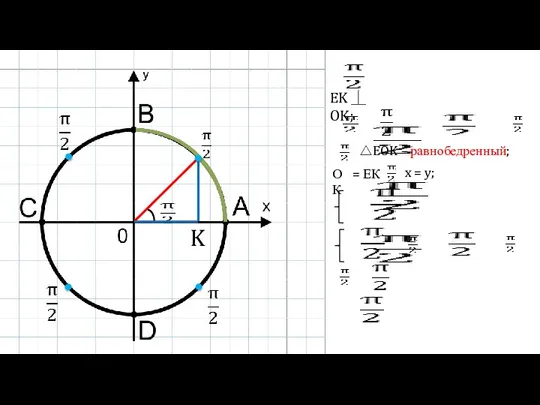
- 2. E (x;y) – точка окружности; –1≤ х ≤ 1; –1≤ у ≤1; уравнение окружности: х2 +
- 3. K EK ⏊ OK; △EOK – равнобедренный; ОК = ЕК x = y;
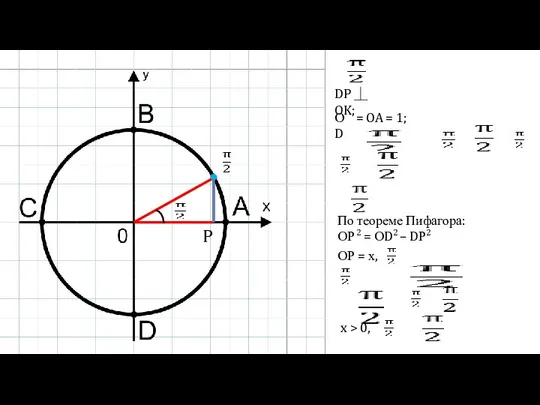
- 4. DP ⏊ OK; P ОD = OA = 1; По теореме Пифагора: ОР 2 = ОD2
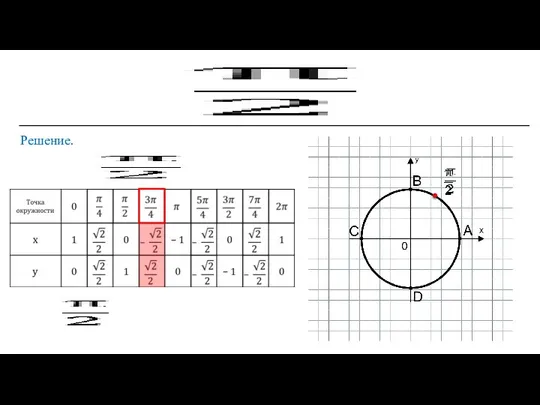
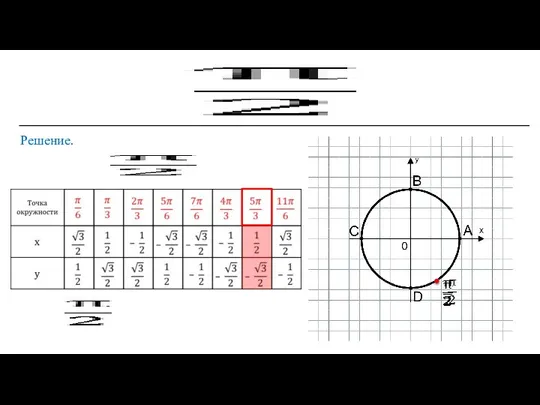
- 6. Решение.
- 7. Если точка D числовой окружности соответствуют числу t, то она соответствует и любому числу вида t
- 8. Решение.
- 9. Решение.
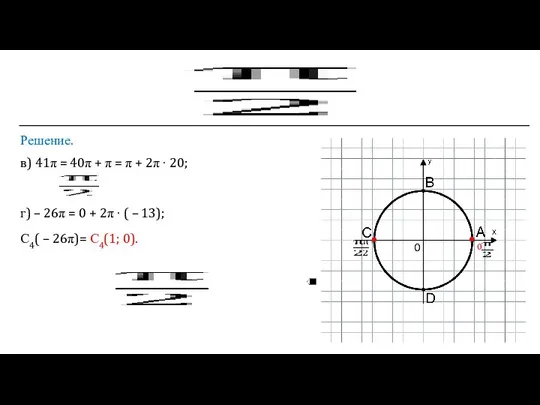
- 10. Решение. в) 41π = 40π + π = π + 2π ∙ 20; г) – 26π
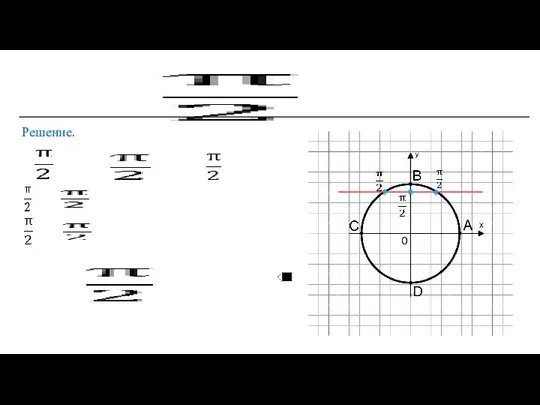
- 11. Решение.
- 13. Скачать презентацию



 Математическое моделирование. Лекция 1
Математическое моделирование. Лекция 1 Проектирование последовательностных схем
Проектирование последовательностных схем Один и много
Один и много Параллельные прямые в пространстве
Параллельные прямые в пространстве Математическая модель игры World of Tanks
Математическая модель игры World of Tanks Презентация на тему Уравнения
Презентация на тему Уравнения 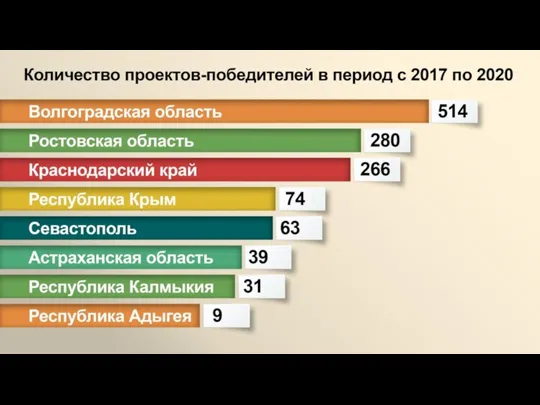 Количество проектов-победителей в период с 2017 по 2020 гг
Количество проектов-победителей в период с 2017 по 2020 гг Обратные тригонометрические функции и их свойства
Обратные тригонометрические функции и их свойства Интеллектуальная игра Самый умный. Информатика. Математика
Интеллектуальная игра Самый умный. Информатика. Математика Перпендикуляр и наклонная к прямой
Перпендикуляр и наклонная к прямой Деление обыкновенных дробей
Деление обыкновенных дробей Л 9 Бесконечно большие функции и замечательные пределы
Л 9 Бесконечно большие функции и замечательные пределы Интегрированный урок математики и краеведения. Путешествие по Кизильскому району. Часть 3
Интегрированный урок математики и краеведения. Путешествие по Кизильскому району. Часть 3 Примеры задач с таблицами истинности
Примеры задач с таблицами истинности Таблица умножения
Таблица умножения Истинностные задачи
Истинностные задачи Чётные и нечётные функции
Чётные и нечётные функции Статистика и ее роль в развитии общества
Статистика и ее роль в развитии общества Запись Арифметических выражений и на языке программирования Паскаль
Запись Арифметических выражений и на языке программирования Паскаль Решение задач на составление линейных алгоритмов
Решение задач на составление линейных алгоритмов Задачи ФИПИ
Задачи ФИПИ Первый признак параллельности прямых
Первый признак параллельности прямых Математика
Математика Цена деления измерительных приборов
Цена деления измерительных приборов Свойства степеней с натуральными показателями
Свойства степеней с натуральными показателями Производная в экономике
Производная в экономике Вынесение множителя из - под знака корня. Внесение множителя под знак корня
Вынесение множителя из - под знака корня. Внесение множителя под знак корня Алгебра в жизни человека
Алгебра в жизни человека