Слайд 2Симметрия
В общем смысле симметрия – это свойство геометрической фигуры, характеризующее некоторую правильность

формы фигуры, неизменность ее при действии, движении и отражении.
Осевая симметрия — это симметрия относительно прямой.
Симметрия является движением.
Слайд 3Осевая симметрия
Фигура называется симметричной относительно прямой а, если для каждой точки фигуры

симметричная ей точка относительно прямой а также принадлежит этой фигуре.
Прямая а называется осью симметрии фигуры.
Слайд 5Прямоугольник
Прямоугольник имеет 2 оси симметрии: прямые, проходящие через точку пересечения диагоналей параллельно

сторонам.
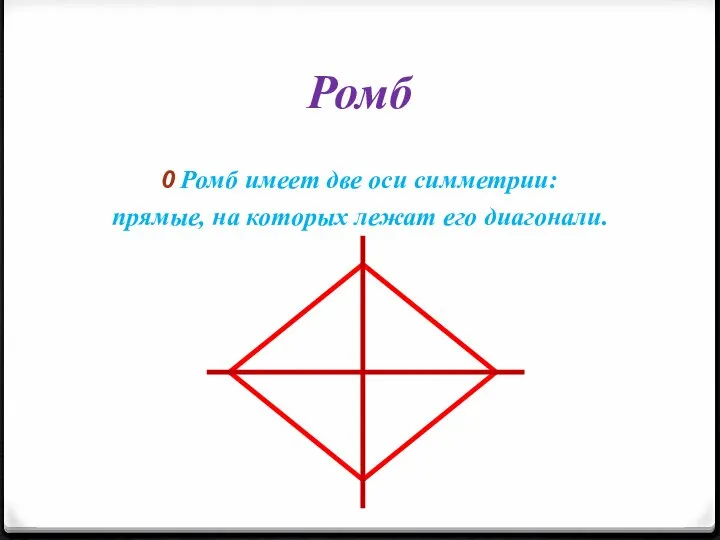
Слайд 6Ромб
Ромб имеет две оси симметрии:
прямые, на которых лежат его диагонали.
Слайд 7Окружность
Окружность имеет бесконечное множество осей симметрии: любая прямая, содержащая диаметр, является осью

симметрии окружности.
Слайд 8Равнобедренная трапеция
Равнобедренная трапеция — фигура, симметричная относительно прямой, перпендикулярной основаниям и проходящей
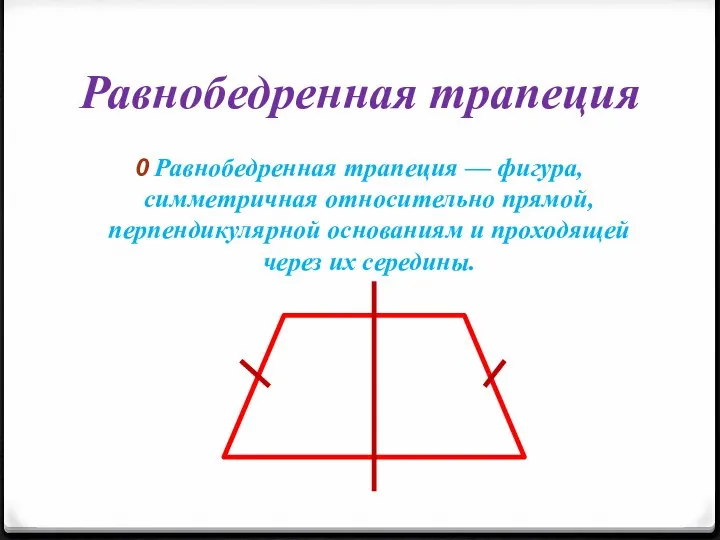
через их середины.
Слайд 9Равнобедренный треугольник
Равнобедренный треугольник имеет одну ось симметрии: прямую, проходящую через высоту (медиану,

биссектрису), проведённую к основанию.
Слайд 10Равносторонний треугольник
Равносторонний треугольник имеет три оси симметрии: прямые, содержащие его высоты (медианы,

биссектрисы).
Слайд 11Угол
Угол — фигура, симметричная относительно прямой, содержащей его биссектрису.

Слайд 12Фигуры, не имеющие симметрии
Имеются фигуры, у которых нет ни одной оси
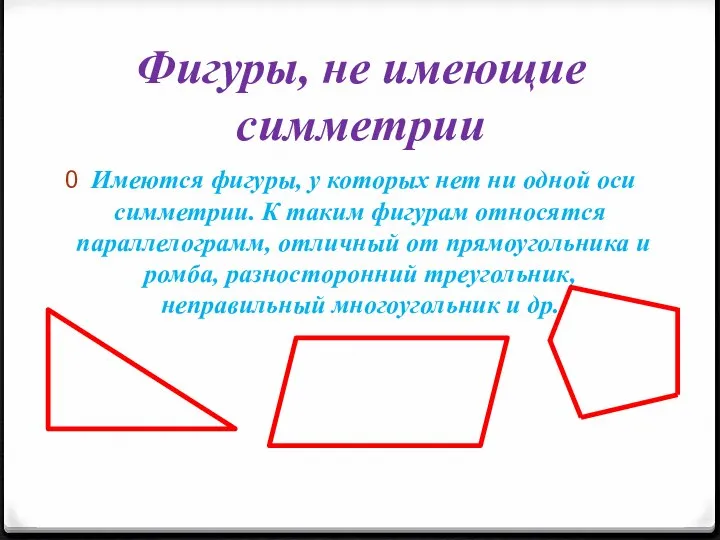
симметрии. К таким фигурам относятся параллелограмм, отличный от прямоугольника и ромба, разносторонний треугольник, неправильный многоугольник и др.











 Экстремум. Условный экстремум функции 2 переменных
Экстремум. Условный экстремум функции 2 переменных Презентация на тему Решение неравенств второй степени с одной переменной
Презентация на тему Решение неравенств второй степени с одной переменной  Квадратный корень
Квадратный корень Уравнение окружности и прямой
Уравнение окружности и прямой Таблица умножения числа 2 и на 2
Таблица умножения числа 2 и на 2 Окружность и круг
Окружность и круг Кривые второго порядка (1)
Кривые второго порядка (1) Думаємо колективно, працюємо оперативно, сперечаємось доказово – це для всіх обов'язково
Думаємо колективно, працюємо оперативно, сперечаємось доказово – це для всіх обов'язково Километр
Километр Элементы комбинаторики. Перестановки
Элементы комбинаторики. Перестановки Таблица сложения
Таблица сложения Построение сечений многогранников
Построение сечений многогранников Число 10
Число 10 Статистика и ее роль в развитии общества
Статистика и ее роль в развитии общества Узоры и орнаменты на посуде
Узоры и орнаменты на посуде Деление
Деление Задачи на построение
Задачи на построение Составление фигур из спичек
Составление фигур из спичек Скрещивающиеся прямые
Скрещивающиеся прямые Уравнение касательной
Уравнение касательной Ягодки для Маши
Ягодки для Маши Теорема Безу (теорема об остатке и разложение на множители)
Теорема Безу (теорема об остатке и разложение на множители) Метод неопределенных коэффициентов
Метод неопределенных коэффициентов Функции нескольких переменных
Функции нескольких переменных Основные и производные единицы системы СИ (ПР 1)
Основные и производные единицы системы СИ (ПР 1) Изопроцессы. Интегрированный урок
Изопроцессы. Интегрированный урок Лекция_04
Лекция_04 Методы решения экстремальных задач
Методы решения экстремальных задач