Понятие функции. Свойства функций

Определение функции
Определение. Пусть каждому числу х из множества чисел Х в силу некоторого (вполне определенного) закона поставлено в соответствие единственное число у. Тогда говорят, что у есть функция от х, определенная на множестве Х и записывают у=f(х) или у(х).
Или, другими словами:
Если каждому значению х из некоторого множества поставлено в соответствие по определенному правилу единственное число у, то говорят, что на этом множестве задана функция от переменной х, и записывают у = f (x) или f(x). При этом х называют независимой переменной или аргументом функции, а у – зависимой переменной или функцией от х.

Область определения, множество значений функции
Определение. Множество значений х (множество Х), для которых определены значения у(х), называют областью определения функции у=f(х) и обозначают D(y) или D(f).
Определение. Множество значений, принимаемых переменной у (множество всех значений зависимой переменной у) называют множеством значений (областью значений) или областью изменения функции у=f(x) и обозначают Е(у) или E(f).

График функции
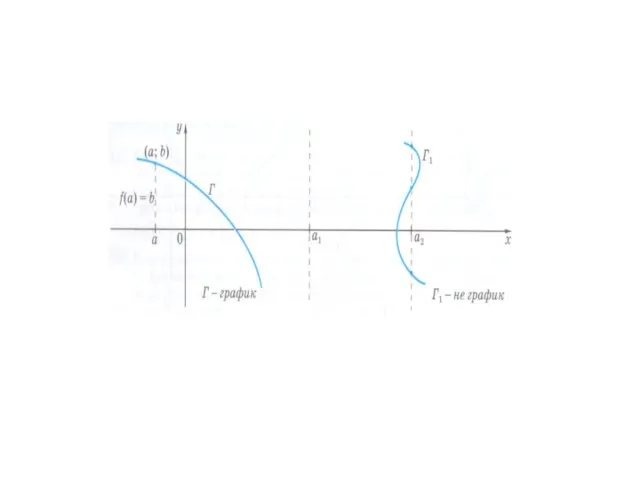
Определение. Графиком функции у=f(х) называют множество всех точек координатной плоскости хОу вида (х; f(x)), где х – любое число из области определения функции.
Или, другими словами
Графиком функции называется геометрическое место точек (ГМТ) плоскости, у которых абсциссами служат значения независимой переменной, а ординатами – соответствующие значения функций, т.е. график – это ГМТ (x; f(x)).

В школьном курсе изучались функции:
Все эти функции называют основными элементарными функциями.
Функции, полученные из основных элементарных функций с помощью конечного числа арифметических операций и применения конечного числа суперпозиций, принято называть элементарными функциями.

2. Табличный способ задания функции
При этом способе задания функции заполняется таблица, в которой даются значения функции для конечного множества значений аргумента. Примерами табличного задания функции являются таблицы квадратов, кубов, квадратных корней и т.д.
Этот способ задания функциональной зависимости удобен для записи результатов наблюдений и измерений в процессе опытов, он распространен в науке, технике, т.е. на практике. Примерами могут служить таблицы измерений температуры пациента в зависимости от времени, зависимости скорости распространения сейсмических волн в толще земной коры от глубины и т.д.

3. Графический способ задания функции
Такое задание дает лишь приближенное значение функции с точностью, которую допускает чтение графика. Чаще всего, графическое задание применяется при обработке наблюдений, когда производится измерение величины, меняющейся при изменении другой величины, играющей роль независимой переменной. Этот способ широко используется в научных исследованиях и в современном производстве.

Определение. Пусть область определения функции у = f(x) является множеством, симметричным относительно начала координат.
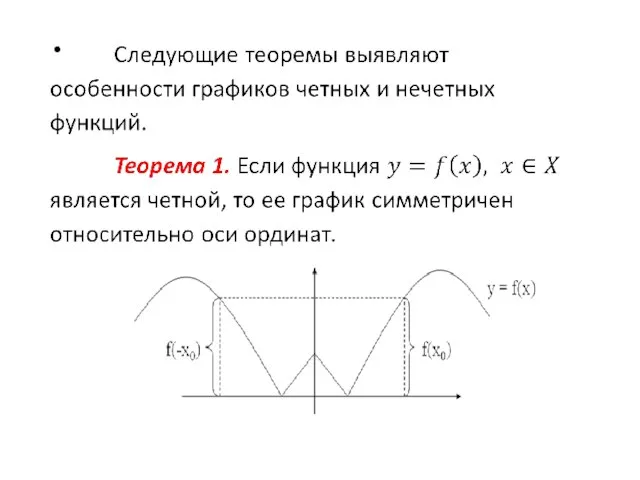
Функция у = f(x) называется четной, если
f(-x) = f(x) для любого х из области определения функции.
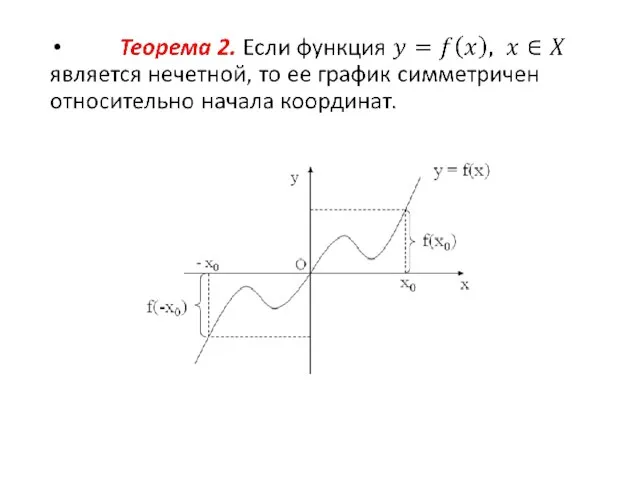
Функция у = f(x) называется нечетной, если
f(-x) = -f(x) для любого х из области определения функции.
Определение. Не нечетную и не четную функцию называют функцией общего вида.

При построении графиков четной и нечетной функций достаточно построить только правую ветвь графика для положительных значений аргумента. Левая ветвь достраивается симметрично относительно начала координат для нечетной функции и относительно оси ординат для четной функции.

20 Монотонность функций
Определение. Функция y = f(x) называется возрастающей в некотором промежутке, если для любых двух значений х из этого промежутка большему значению аргумента соответствует большее значение функции, т.е. из условия x1 < x2 следует, что f(x1) < f(x2) для любых x1 и x2 из данного промежутка.

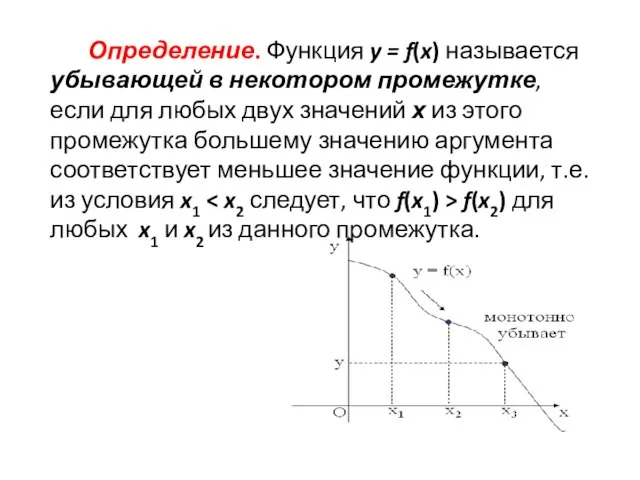
Определение. Функция y = f(x) называется убывающей в некотором промежутке, если для любых двух значений х из этого промежутка большему значению аргумента соответствует меньшее значение функции, т.е. из условия x1 < x2 следует, что f(x1) > f(x2) для любых x1 и x2 из данного промежутка.

Возрастающие и убывающие функции называются монотонными функциями.
При движении вдоль оси абсцисс слева направо ордината графика возрастающей функции увеличивается, а ордината убывающей – уменьшается.

При исследовании функции на возрастание или убывание в некотором промежутке сначала надо проверить, задана ли функция в этом промежутке. Чаще всего, функция y = f(x) не является возрастающей (или убывающей) во всей области ее определения, но из области определения обычно можно указать промежутки, на которых функция является возрастающей (или убывающей). Их называют промежутками монотонности.

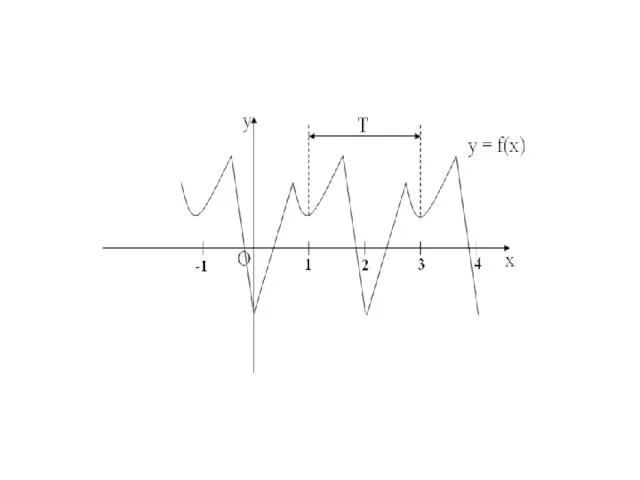
Определение. Наименьший из множества положительных периодов функции называется основным периодом.
Примерами периодических функций служат все тригонометрические функции.
Периодической является и всякая постоянная функция, причем ее периодом служит любое ненулевое число. Например: y = 2; y = 10.

40 Асимптоты графиков функций
Определение. Горизонтальная или наклонная прямая называются асимптотой графика функции y = f(x) при х → ± ∞, если при х → ± ∞ расстояние от точки графика до точки с той же абсциссой, лежащей на прямой, стремится к нулю.

II способ (относится к дробно-рациональным функциям):
Если степень числителя дробно-рациональной функции равна степени знаменателя или больше степени знаменателя на единицу, то график этой функции имеет асимптоту, в первом случае – горизонтальную, во втором случае – наклонную. Чтобы найти эту асимптоту, надо выделить из дроби целую часть.
Эта целая часть в первом случае окажется числом b, во втором – многочленом первой степени kx + b. Уравнения y = b, y = kx + b и являются уравнениями искомых асимптот, в первом случае – горизонтальной, во втором – наклонной.