Понятие многогранника. Призма

При́зма : лат. prisma от др.-греч. πρίσμα «нечто отпиленное»

На уроке
мы узнаем:
что такое геометрическое тело и многогранники;
элементы и виды многогранников, их свойства;
теорему Эйлера;
что такое призма;
элементы призмы и виды призм;
свойства боковых граней призмы и боковых ребер призмы;
мы научимся:
отличать многогранники от других геометрических тел;
различать выпуклые и невыпуклые многогранники;
отличать призмы от других геометрических тел;
выделять элементы призмы;
мы сможем:
приводить примеры реальных объектов, моделями которых являются многогранники.

Устно ответить на вопросы:
1) Сумма углов треугольника.
Сумма углов треугольника равна 180°.
2) Свойства углов при основании равнобедренного треугольника.
В равнобедренном треугольнике углы при основании равны.

3) Чему равны острые углы равнобедренного прямоугольного треугольника?
45о
4) Свойство катета, лежащего против угла в 30о .
Катет прямоугольного треугольника, лежащий против угла в 30° , равен половине гипотенузы (гипотенуза в два раза длиннее катета, лежащего против угла в 30°)

5) Что называется углом между прямой и плоскостью?
Угол между прямой и плоскостью — это угол между прямой и ее проекцией на эту плоскость.
6) Что называется линейным углом двугранного угла?
Линейным углом двугранного угла называется угол, сторонами которого являются лучи, по которым грани двугранного угла пересекаются плоскостью, перпендикулярной ребру двугранного угла.

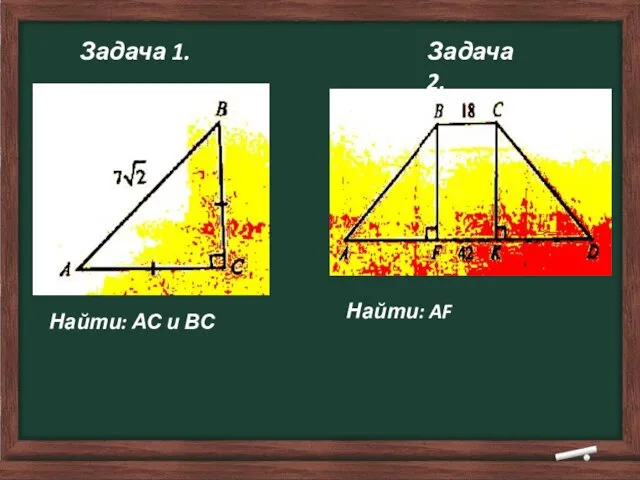
Задача 1.
Задача 2.
Найти: АС и ВС
Найти: AF

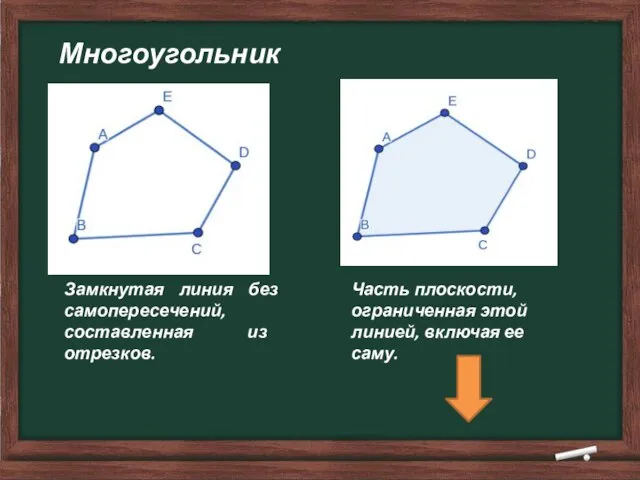
Многоугольник
Замкнутая линия без самопересечений, составленная из отрезков.
Часть плоскости, ограниченная этой линией, включая ее саму.

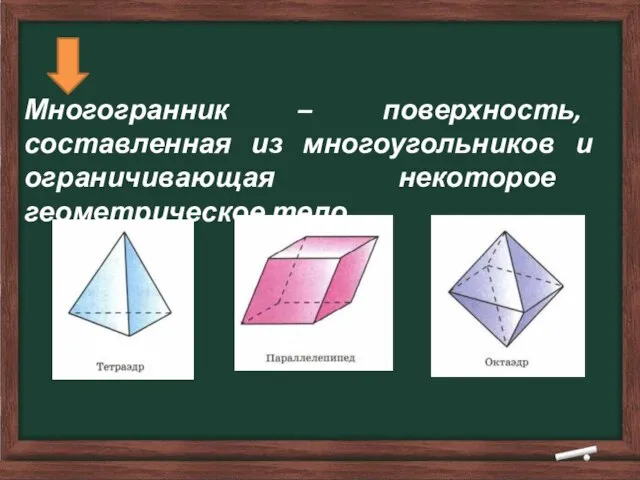
Многогранник – поверхность, составленная из многоугольников и ограничивающая некоторое геометрическое тело.

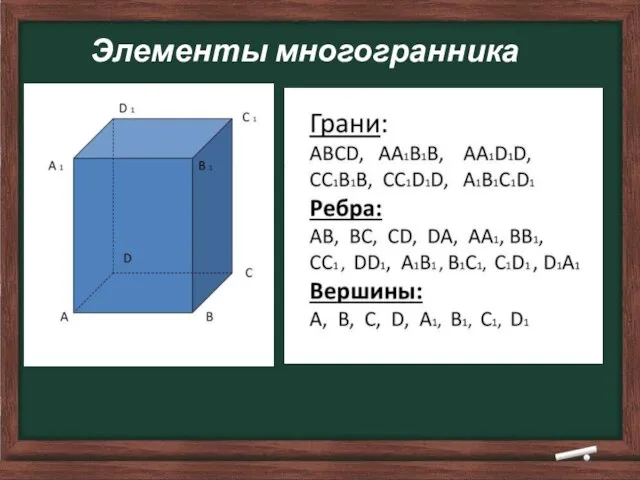
Элементы многогранника

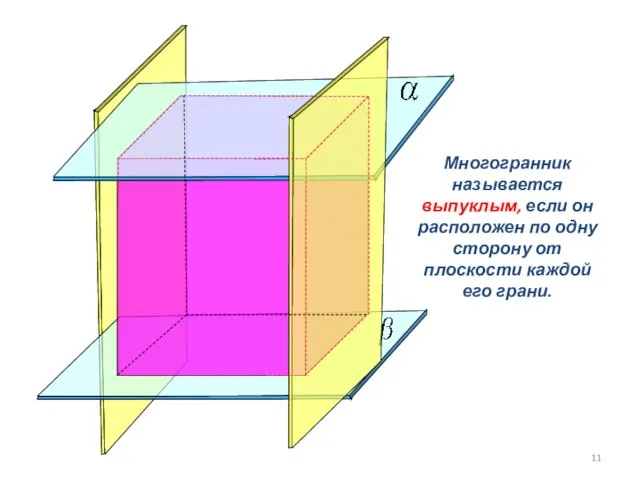
Многогранник называется выпуклым, если он расположен по одну сторону от плоскости каждой его грани.

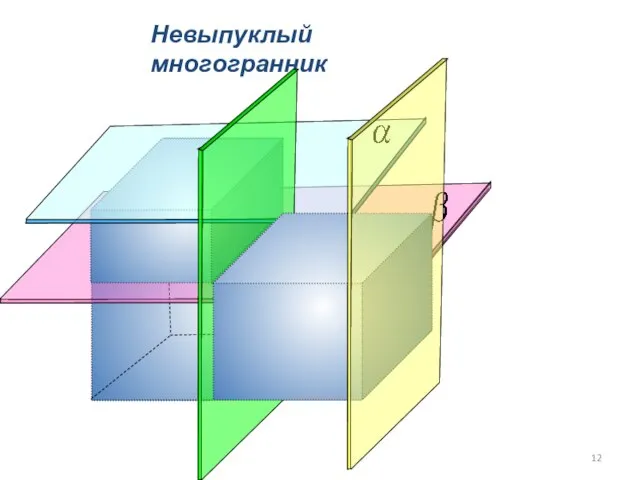
Невыпуклый многогранник

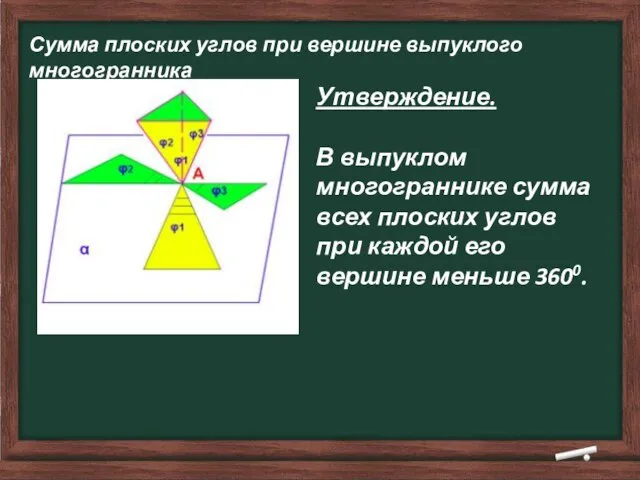
Сумма плоских углов при вершине выпуклого многогранника
Утверждение.
В выпуклом многограннике сумма всех плоских углов при каждой его вершине меньше 3600.

Теорема Эйлера.
Пусть
В – число вершин выпуклого многогранника,
Р – число его ребер,
Г – число его граней.
Тогда верно равенство В – Р + Г= 2.

Заполнить таблицу:

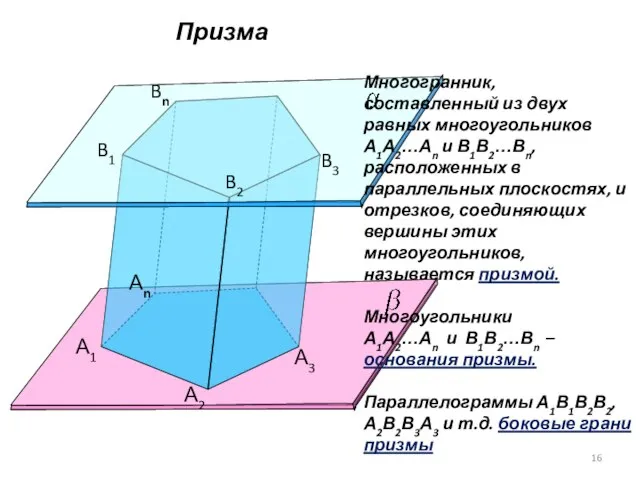
Призма
А1
А2
Аn
B1
B2
Bn
B3
А3
Многогранник, составленный из двух равных многоугольников А1А2…Аn и В1В2…Вn, расположенных в параллельных плоскостях, и отрезков, соединяющих вершины этих многоугольников, называется призмой.
Многоугольники
А1А2…Аn и В1В2…Вn – основания призмы.
Параллелограммы А1В1В2В2, А2В2В3А3 и т.д. боковые грани призмы

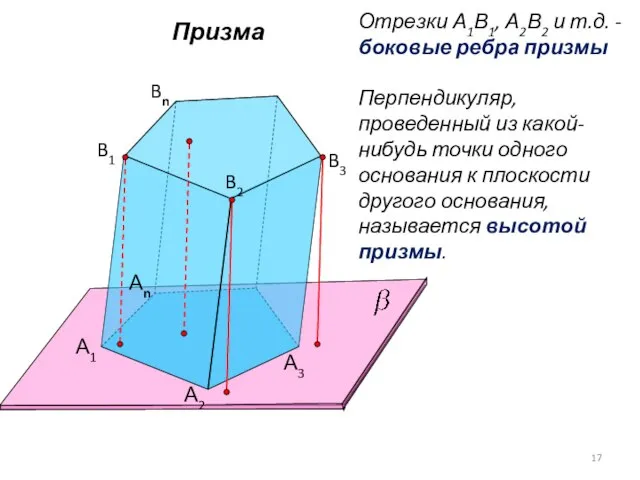
Призма
А1
А2
Аn
B1
B2
Bn
B3
А3
Отрезки А1В1, А2В2 и т.д. -
боковые ребра призмы
Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы.

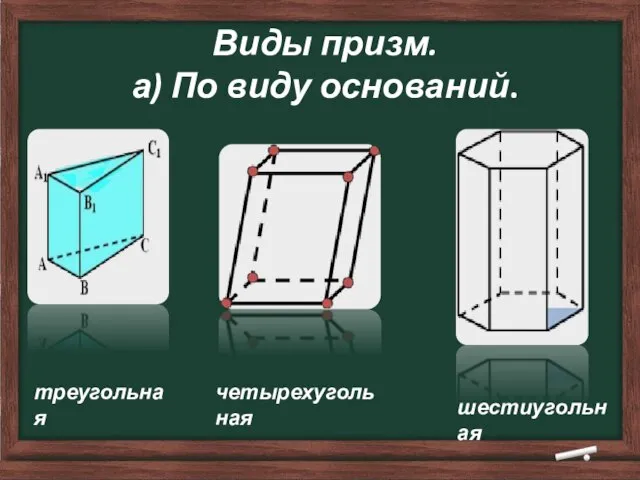
Виды призм.
а) По виду оснований.
треугольная
четырехугольная
шестиугольная

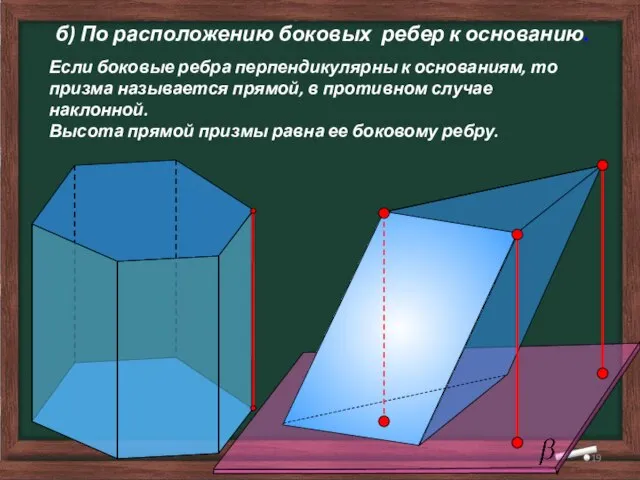
Если боковые ребра перпендикулярны к основаниям, то призма называется прямой, в противном случае наклонной.
Высота прямой призмы равна ее боковому ребру.
б) По расположению боковых ребер к основанию.

Прямая призма называется правильной, если ее основания - правильные многоугольники. У такой призмы все боковые грани – равные прямоугольники.

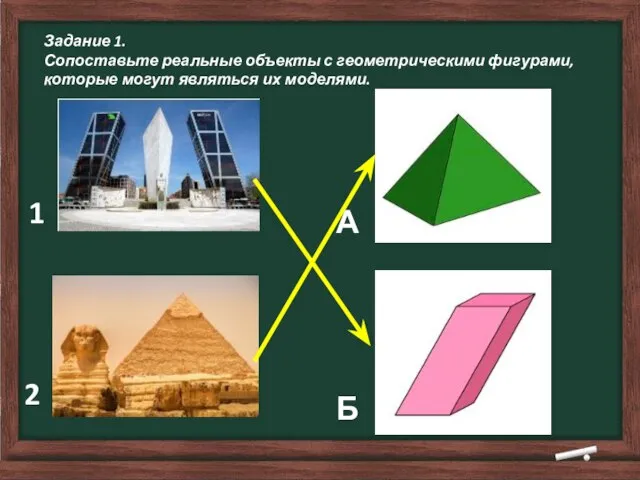
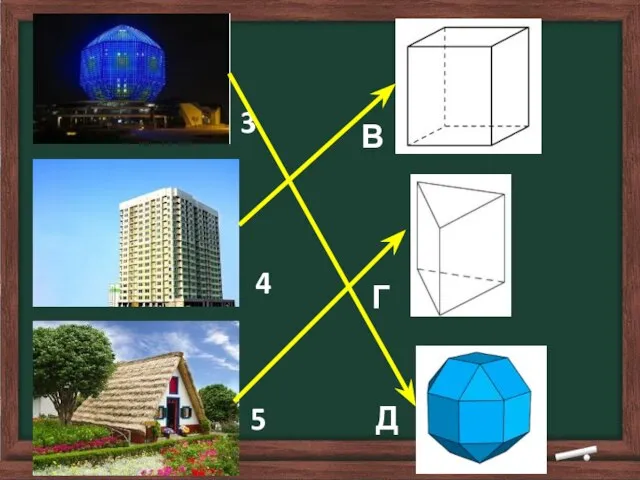
Задание 1.
Сопоставьте реальные объекты с геометрическими фигурами, которые могут являться их моделями.
1
2
А
Б

3
4
5
В
Г
Д

Задание 2.
Используя рисунок, посчитайте у данного многогранника количество вершин:
ребер:
граней:
Количество боковых ребер:
количество боковых граней:
10
15
7
5
5

Решить на доске и в тетрадях:
№219, 220, 223.
Домашнее задание:
п. 27 – 30. №295.

Подведение итогов
Продолжи предложение: