ЕГЭ 2014. Задачи первой и второй части (Вариант 45)

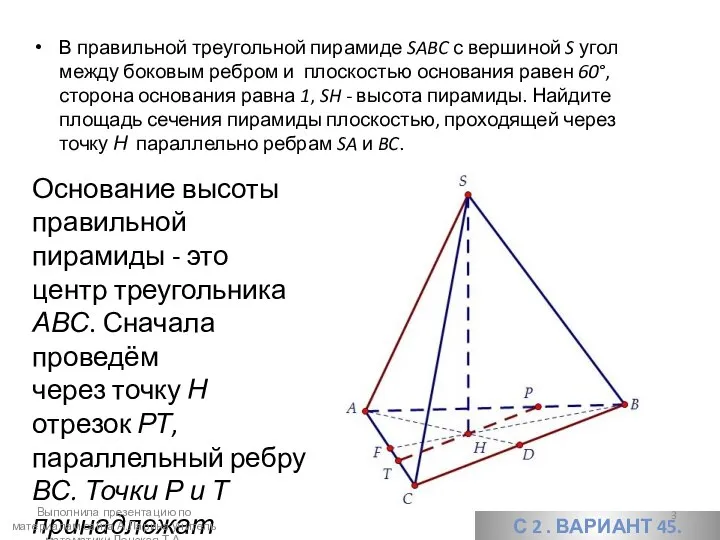
С 2 . ВАРИАНТ 45.
В правильной треугольной пирамиде SABC с вершиной S угол между боковым ребром и плоскостью основания равен 60°, сторона основания равна 1, SH - высота пирамиды. Найдите площадь сечения пирамиды плоскостью, проходящей через точку Н параллельно ребрам SA и BC.
Выполнила презентацию по материалам сайта А.Ларина учитель математики Лонская Т.А.

В правильной треугольной пирамиде SABC с вершиной S угол между боковым ребром и плоскостью основания равен 60°, сторона основания равна 1, SH - высота пирамиды. Найдите площадь сечения пирамиды плоскостью, проходящей через точку Н параллельно ребрам SA и BC.
Основание высоты правильной пирамиды - это центр треугольника АВС. Сначала проведём
через точку Н отрезок РТ, параллельный ребру ВС. Точки Р и Т принадлежат сечению.
С 2 . ВАРИАНТ 45.
Выполнила презентацию по материалам сайта А.Ларина учитель математики Лонская Т.А.

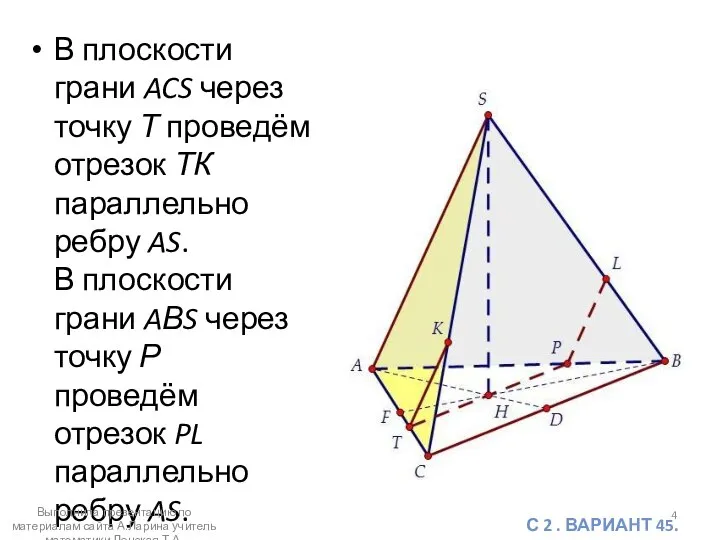
В плоскости грани ACS через точку Т проведём отрезок ТК параллельно ребру AS.
В плоскости грани AВS через точку Р проведём отрезок PL параллельно ребру AS.
С 2 . ВАРИАНТ 45.
Выполнила презентацию по материалам сайта А.Ларина учитель математики Лонская Т.А.

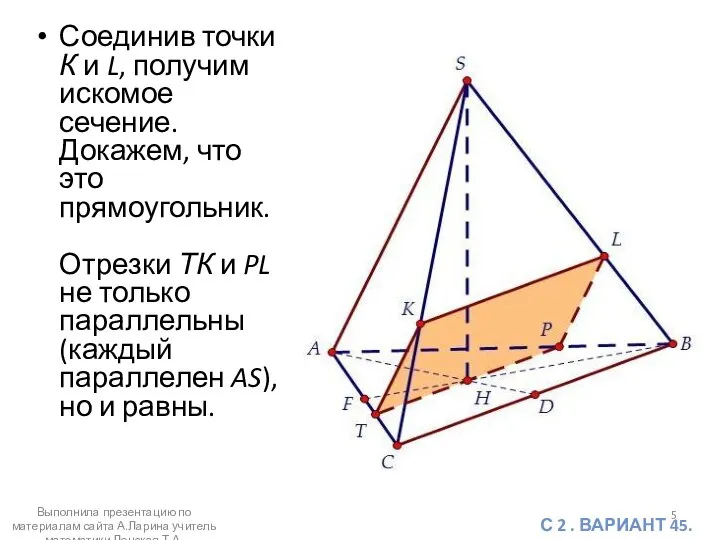
Соединив точки К и L, получим искомое сечение. Докажем, что это прямоугольник. Отрезки ТК и PL не только параллельны (каждый параллелен AS), но и равны.
С 2 . ВАРИАНТ 45.
Выполнила презентацию по материалам сайта А.Ларина учитель математики Лонская Т.А.

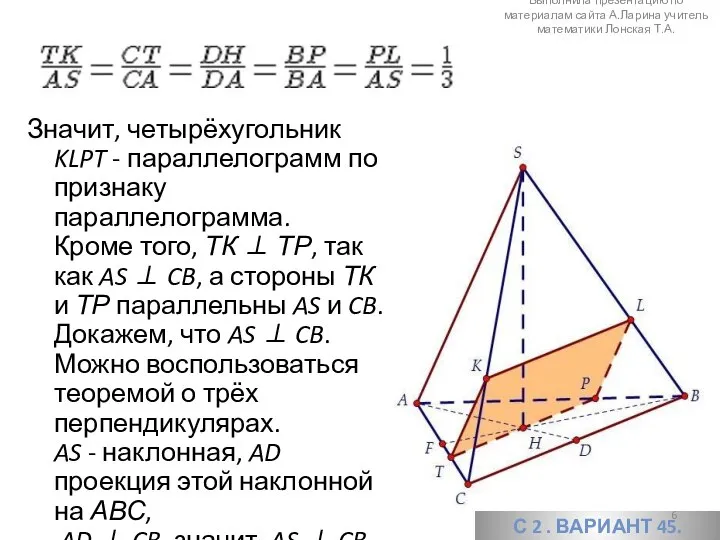
Значит, четырёхугольник KLPT - параллелограмм по признаку параллелограмма.
Кроме того, ТК ⊥ ТР, так как AS ⊥ CB, а стороны ТК и ТР параллельны AS и CB.
Докажем, что AS ⊥ CB. Можно воспользоваться теоремой о трёх перпендикулярах.
AS - наклонная, AD проекция этой наклонной на АВС,
AD ⊥ CB, значит, AS ⊥ CB.
С 2 . ВАРИАНТ 45.
Выполнила презентацию по материалам сайта А.Ларина учитель математики Лонская Т.А.

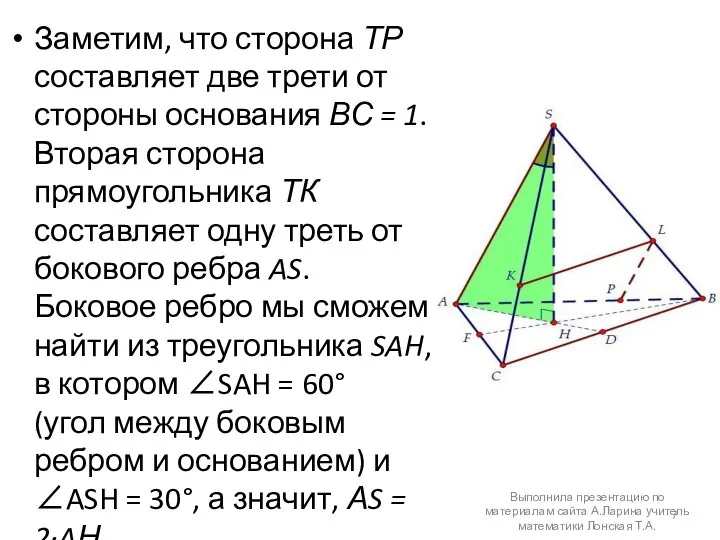
Заметим, что сторона ТР составляет две трети от стороны основания ВС = 1.
Вторая сторона прямоугольника ТК составляет одну треть от бокового ребра AS.
Боковое ребро мы сможем найти из треугольника SAH, в котором ∠SAH = 60°
(угол между боковым ребром и основанием) и ∠ASH = 30°, а значит, АS = 2·AН.
Выполнила презентацию по материалам сайта А.Ларина учитель математики Лонская Т.А.

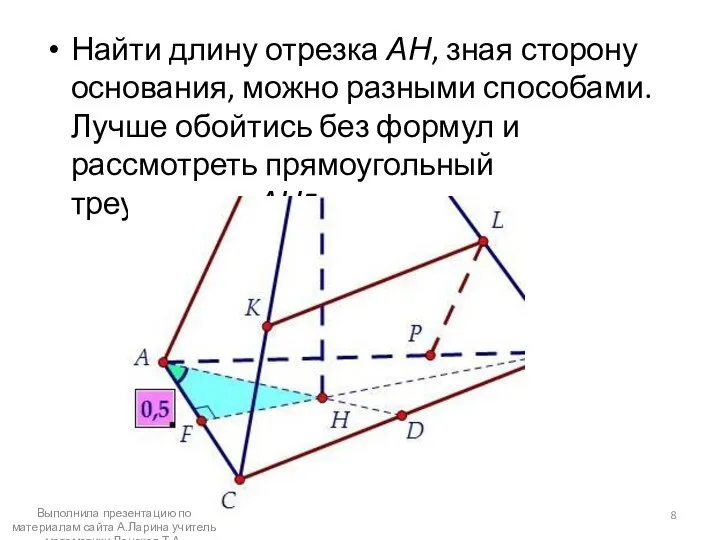
Найти длину отрезка АН, зная сторону основания, можно разными способами.
Лучше обойтись без формул и рассмотреть прямоугольный треугольник АНF.
Выполнила презентацию по материалам сайта А.Ларина учитель математики Лонская Т.А.

С 2 . ВАРИАНТ 45.
Выполнила презентацию по материалам сайта А.Ларина учитель математики Лонская Т.А.

В 3. ВАРИАНТ 45.
Основания равнобедренной трапеции равны 6 и 12. Синус острого угла трапеции равен 0,8. Найдите боковую сторону.
ОТВЕТ : 5.
Выполнила презентацию по материалам сайта А.Ларина учитель математики Лонская Т.А.

Выполнила презентацию по материалам сайта А.Ларина учитель математики Лонская Т.А.
В 5. ВАРИАНТ 45.
ОТВЕТ : 0.

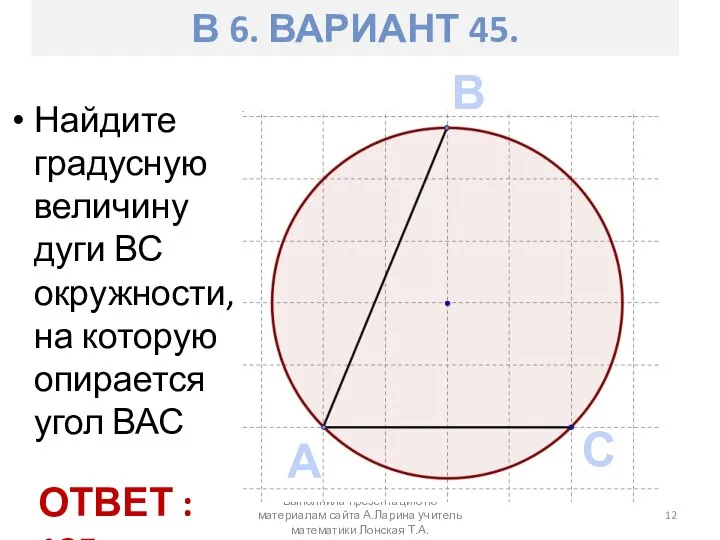
Найдите градусную величину дуги ВС окружности, на которую опирается угол ВАС
Выполнила презентацию по материалам сайта А.Ларина учитель математики Лонская Т.А.
В 6. ВАРИАНТ 45.
А
В
С
ОТВЕТ : 135

Выполнила презентацию по материалам сайта А.Ларина учитель математики Лонская Т.А.
В 7. ВАРИАНТ 45.
ОТВЕТ : 6

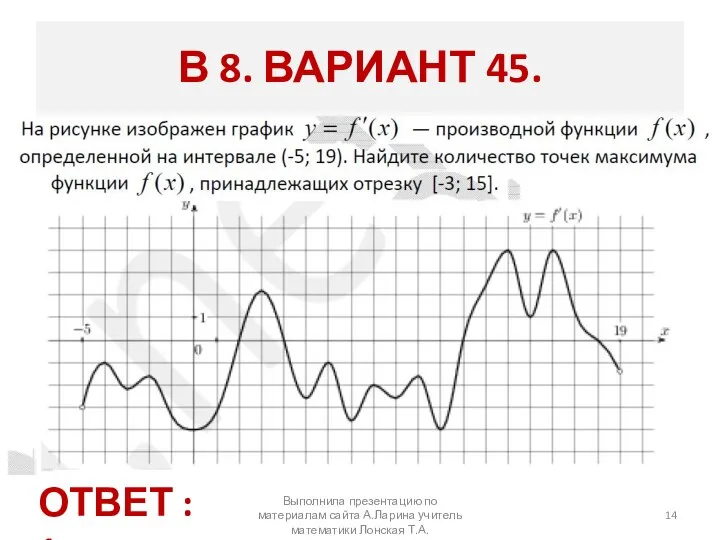
Выполнила презентацию по материалам сайта А.Ларина учитель математики Лонская Т.А.
В 8. ВАРИАНТ 45.
ОТВЕТ : 1

Выполнила презентацию по материалам сайта А.Ларина учитель математики Лонская Т.А.
В 9. ВАРИАНТ 45.
ОТВЕТ : 6

Выполнила презентацию по материалам сайта А.Ларина учитель математики Лонская Т.А.
В 12. ВАРИАНТ 45.
ОТВЕТ : 0,33

Выполнила презентацию по материалам сайта А.Ларина учитель математики Лонская Т.А.
В 14. ВАРИАНТ 45.
ОТВЕТ : 67,75

Выполнила презентацию по материалам сайта А.Ларина учитель математики Лонская Т.А.
С 3. ВАРИАНТ 45.
ОТВЕТ : (2;3)

Выполнила презентацию по материалам сайта А.Ларина учитель математики Лонская Т.А.
С 5. ВАРИАНТ 45.
ОТВЕТ :