Содержание
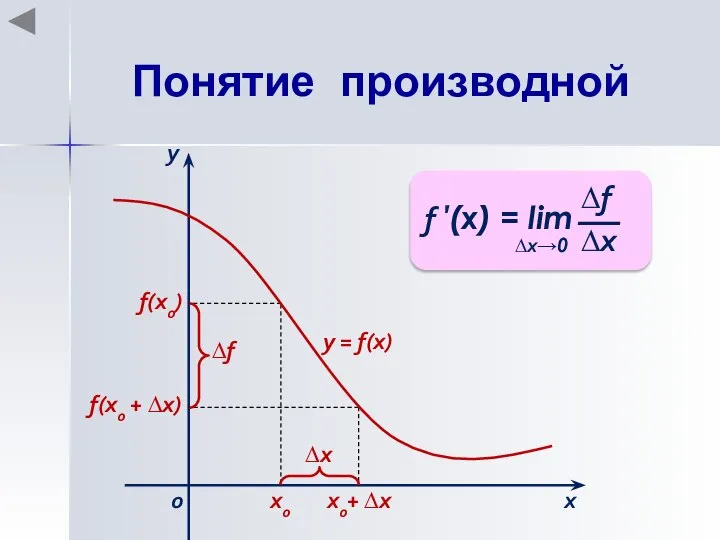
- 2. Понятие производной Производной функции у = f(x), заданной на некотором интервале (a; b), в некоторой точке
- 3. Понятие производной х0 х0+ ∆х f(x0) f(x0 + ∆х) ∆х х у 0 ∆f у =
- 4. Зафиксировать значение х0, найти f(x0). Дать аргументу х0 приращение ∆х, перейти в новую точку х0 +
- 5. Примеры 1. Найти производную функции y = kx + b в точке хo
- 6. Примеры 2. Найти производную функции y = C (C – const) в точке хo
- 7. Примеры 3. Найти производную функции y = x2 в точке хo
- 8. Примеры
- 9. Примеры
- 10. Примеры 5. Найти производную функции y = 1/x в точке хo
- 11. Примеры 5. Найти производную функции y = 1/x в точке хo
- 12. Физический ( механический ) смысл производной Если при прямолинейном движении путь s, пройденный точкой, есть функция
- 13. Если функция имеет производную (дифференцируема) в точке х, то она непрерывна в этой точке.
- 14. Прочитайте п.4.1, обратите внимание на понятия выделенные в розовых рамках Стр92,94.. Рассмотрите примеры в учебнике и
- 16. Скачать презентацию












 Построение треугольников по трем элементам
Построение треугольников по трем элементам Математическая статистика
Математическая статистика Параллельные и перпендикулярные прямые
Параллельные и перпендикулярные прямые ОГЭ. Приемы решения практикоориентированных задач
ОГЭ. Приемы решения практикоориентированных задач Сумма углов треугольника
Сумма углов треугольника Повторение. Числа от 100 до 1000 (Урок 1)
Повторение. Числа от 100 до 1000 (Урок 1) Случайные величины
Случайные величины Линейные неравенства. 8 класс
Линейные неравенства. 8 класс Учимся писать цифры
Учимся писать цифры Решение уравнений
Решение уравнений Презентация на тему Математическая мозаика
Презентация на тему Математическая мозаика  Сложение чисел
Сложение чисел Презентация на тему Решение диофантовых уравнений
Презентация на тему Решение диофантовых уравнений  Задачи на координатной плоскости
Задачи на координатной плоскости У мольберта - математик
У мольберта - математик Презентация на тему Понятие площади фигуры и ее измерение
Презентация на тему Понятие площади фигуры и ее измерение  Коллекция игр. 1 класс
Коллекция игр. 1 класс Razonamiento. Matemático práctica
Razonamiento. Matemático práctica Величины
Величины Неопределенный интеграл Ч2, свойства неопределенного интеграла
Неопределенный интеграл Ч2, свойства неопределенного интеграла Уравнение. Решение уравнений способом подбора. Математика, 2 класс
Уравнение. Решение уравнений способом подбора. Математика, 2 класс Основные тригонометрические тождества
Основные тригонометрические тождества Формула Бернулли
Формула Бернулли Моменты случайной величины
Моменты случайной величины Цифровые средства измерения
Цифровые средства измерения Формулы сокращенного умножения. Тренажер
Формулы сокращенного умножения. Тренажер Определитель 3 порядка
Определитель 3 порядка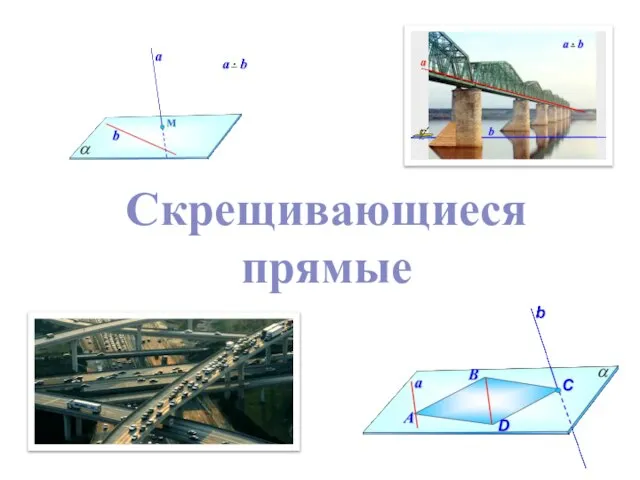 Скрещивающиеся прямые
Скрещивающиеся прямые