Содержание
- 2. 1. Находить особо важные точки графика: - стационарные и критические точки; - точки экстремума; - точки
- 3. Необходимое оборудование, материалы и вспомогательные средства:
- 4. Мордкович А.Г. Алгебра и начала математического анализа. Часть 1. Учебник. – М., 2008. Мордкович А.Г. Алгебра
- 5. Найти область определения функции; Исследовать функцию на чётность; Найти асимптоты; Найти стационарные и критические точки; Найти
- 6. Рассмотрим пример. Построить график функции у = 1. Область определения функции это все допустимые значения аргумента:
- 7. Исследуя функцию по схеме, составим таблицу.
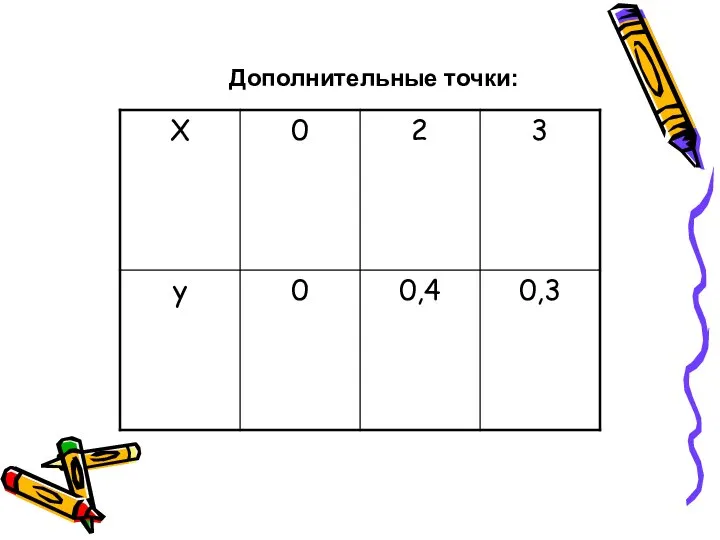
- 8. Дополнительные точки:
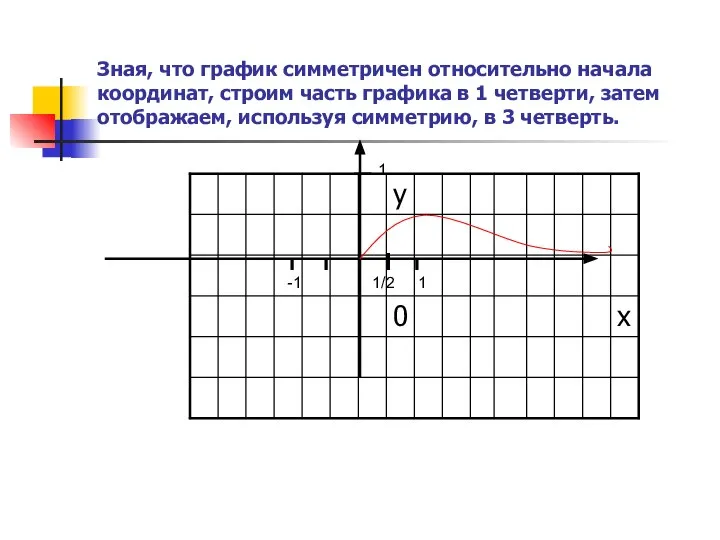
- 9. Зная, что график симметричен относительно начала координат, строим часть графика в 1 четверти, затем отображаем, используя
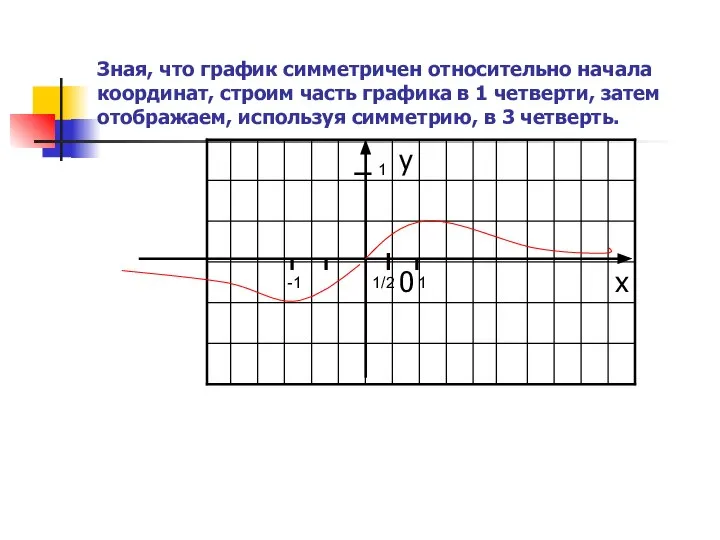
- 10. Зная, что график симметричен относительно начала координат, строим часть графика в 1 четверти, затем отображаем, используя
- 11. Тест 1. Точки минимума и максимума это а) точки экстремума, б) стационарные точки, в) критические точки.
- 13. Скачать презентацию






 Умножение трёхзначного числа на однозначное
Умножение трёхзначного числа на однозначное Свойство биссектрисы угла
Свойство биссектрисы угла Виды моделирования
Виды моделирования Презентация на тему Число и цифра 5
Презентация на тему Число и цифра 5  Теория игр
Теория игр Презентация на тему Почему нельзя жить без математики?
Презентация на тему Почему нельзя жить без математики?  Символика и терминология. Системы координат. Лекция 1
Символика и терминология. Системы координат. Лекция 1 Розв`язок задач
Розв`язок задач Геометрические фигуры
Геометрические фигуры Решение задач на применение признаков равенства треугольников
Решение задач на применение признаков равенства треугольников Показательная функция, её свойства и график
Показательная функция, её свойства и график Блиц - турнир
Блиц - турнир Прямая и отрезки
Прямая и отрезки Множества натуральных чисел
Множества натуральных чисел Зачем изучать математику?
Зачем изучать математику? Построение графиков элементарных функций
Построение графиков элементарных функций Построение перпендикуляра и параллельных прямых
Построение перпендикуляра и параллельных прямых Тема урока: « Закрепление вычислительных навыков, сравнения чисел. Нумерация в пределах 100.»
Тема урока: « Закрепление вычислительных навыков, сравнения чисел. Нумерация в пределах 100.» Вероятностные распределения в ППП Арена
Вероятностные распределения в ППП Арена Презентация на тему Комбинаторные задачи: размещения
Презентация на тему Комбинаторные задачи: размещения  Разложение вектора по двум неколлинеарным векторам
Разложение вектора по двум неколлинеарным векторам Координатная плоскость. Математика 6 класс
Координатная плоскость. Математика 6 класс Матрицы и действия над ними
Матрицы и действия над ними Элементы теории вероятности
Элементы теории вероятности Алгебра. Задачник, часть 2
Алгебра. Задачник, часть 2 Решение задач
Решение задач Презентация на тему Четырехугольники вокруг нас
Презентация на тему Четырехугольники вокруг нас  Параллельные прямые
Параллельные прямые