Содержание
- 2. Построение сечений Построение сечений многогранников можно осуществлять на основании аксиом стереометрии и теорем о параллельности прямых
- 3. Построение сечений Построение на основании аксиом стереометрии и теорем о параллельности прямых и плоскостей -Задача №1
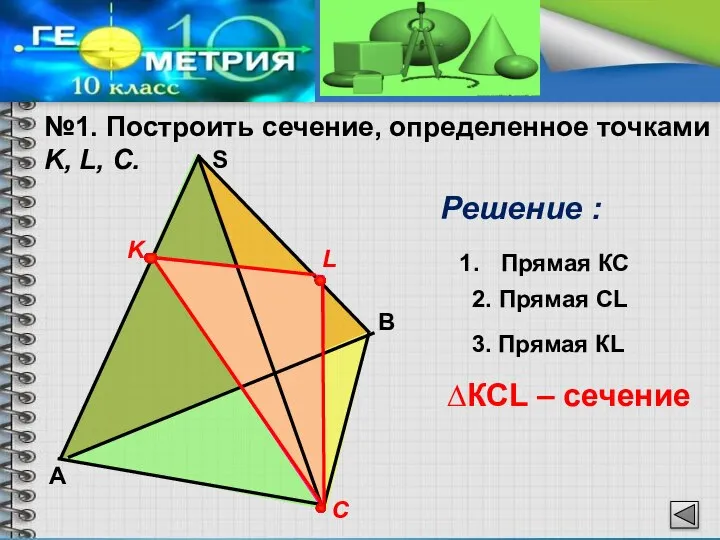
- 4. №1. Построить сечение, определенное точками K, L, С. Решение : K С L Прямая КС 2.
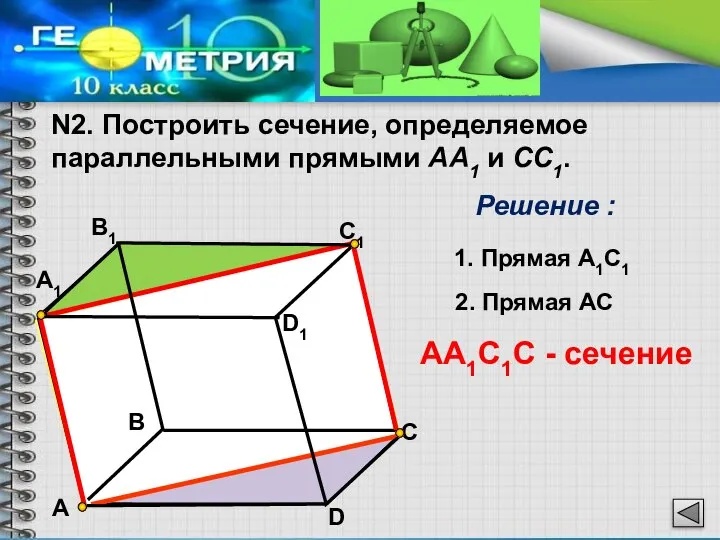
- 5. N2. Построить сечение, определяемое параллельными прямыми АА1 и CC1. А1 В1 С1 D1 С В D
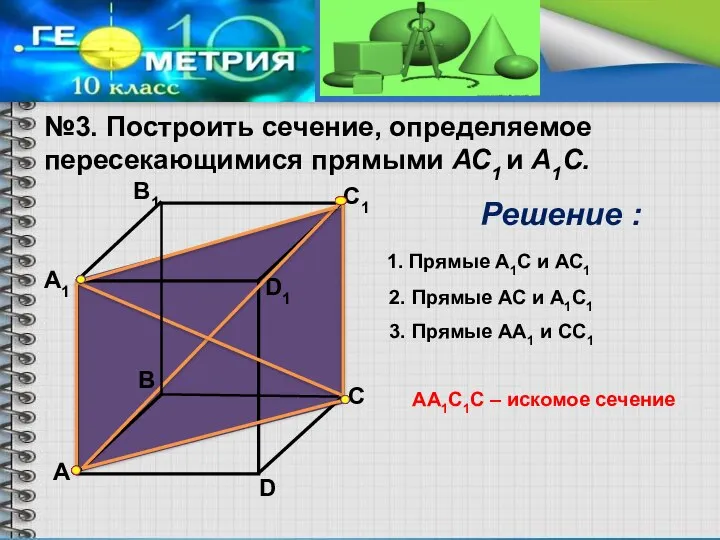
- 6. №3. Построить сечение, определяемое пересекающимися прямыми АС1 и А1С. А А1 В1 С1 D1 D В
- 7. Метод следов Прямая, по которой секущая плоскость α пересекает плоскость основания многогранника, называется следом плоскости α
- 8. Метод следов -Задача №4 -Задача №5 Построение сечений
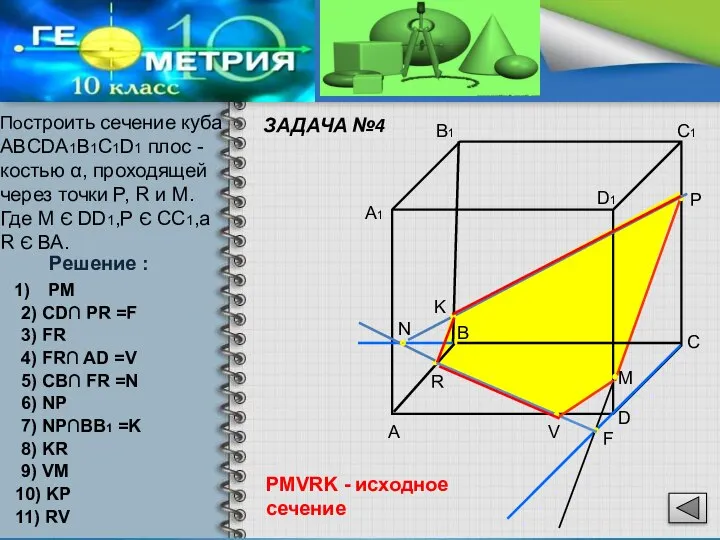
- 9. ЗАДАЧА №4 Построить сечение куба ABCDA1B1C1D1 плос -костью α, проходящей через точки P, R и M.
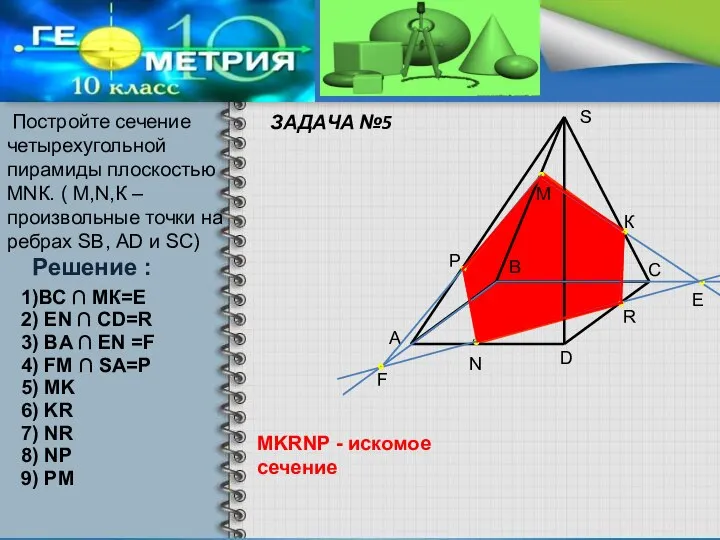
- 10. ЗАДАЧА №5 Постройте сечение четырехугольной пирамиды плоскостью МNК. ( М,N,К – произвольные точки на ребрах SВ,
- 11. Комбиниро-ванный метод Сущность этого метода состоит в том, что на некоторых этапах построения сечения применяется или
- 12. Метод внутреннего проектирования -Задача №6 -Задача №7 Комбинированный метод -Задача №8 Построение сечений
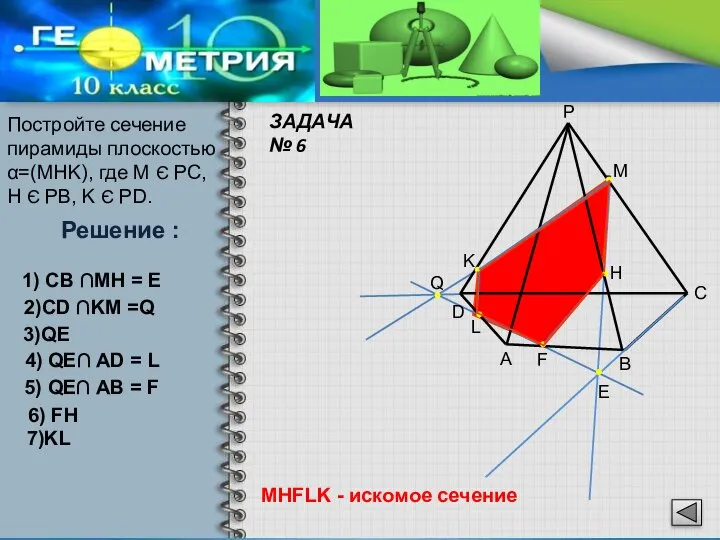
- 13. Постройте сечение пирамиды плоскостью α=(MHK), где M Є PC, H Є PB, K Є PD. D
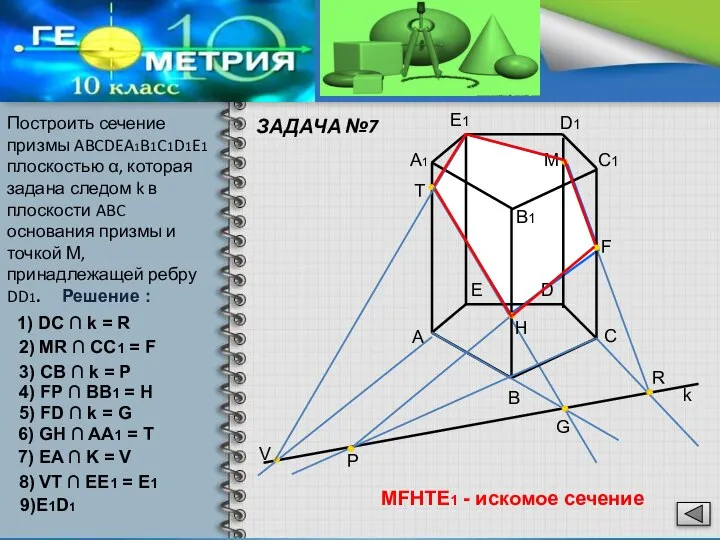
- 14. ЗАДАЧА №7 Решение : Построить сечение призмы ABCDEA1B1C1D1E1 плоскостью α, которая задана следом k в плоскости
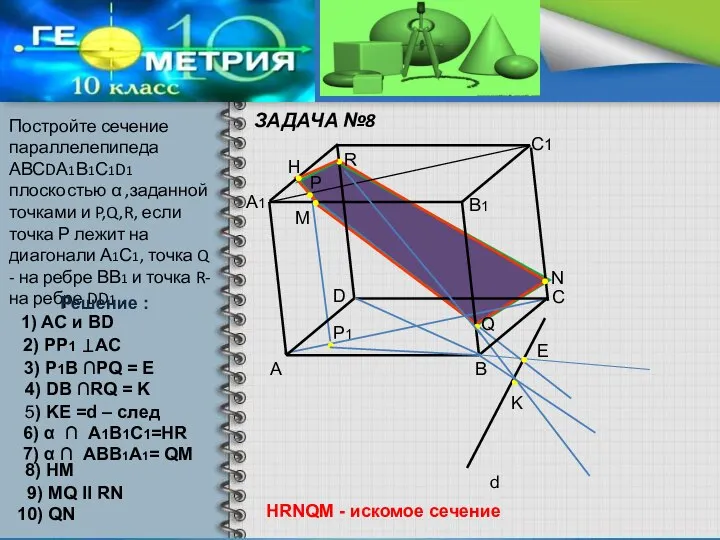
- 15. ЗАДАЧА №8 Постройте сечение параллелепипеда АВСDА1В1С1D1 плоскостью α ,заданной точками и P,Q,R, если точка Р лежит
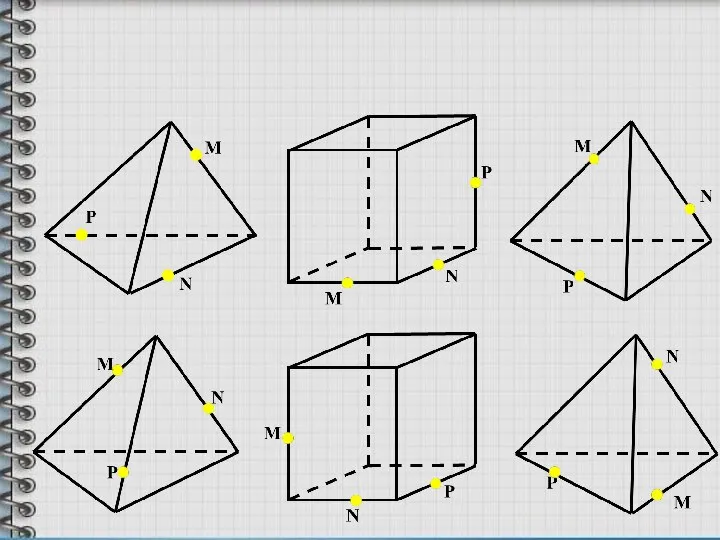
- 16. Самостоятельная работа. (с последующей проверкой)
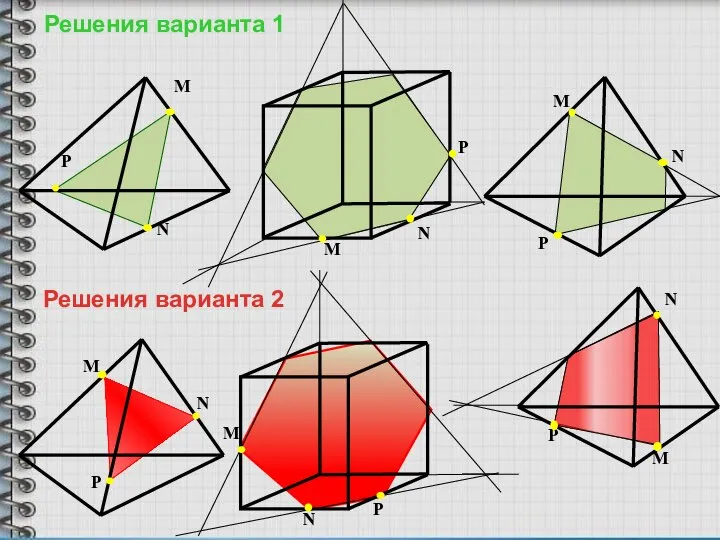
- 17. M N P M N P M N P Решения варианта 1 Решения варианта 2 M
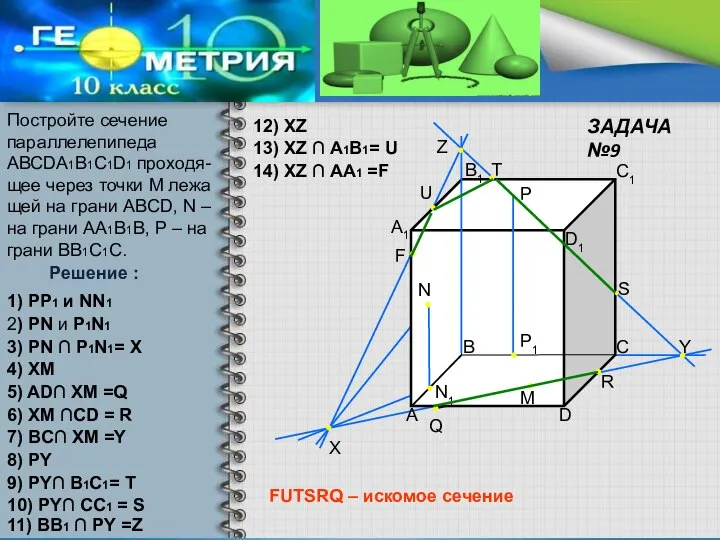
- 18. A A1 B B1 C C1 D D1 X N Y F U T Z M
- 20. Скачать презентацию






 Аттестационная работа. Решение сложных задач по математике
Аттестационная работа. Решение сложных задач по математике Развитие учебных навыков через применение наглядных пособий и перевода математических задач в практическую плоскость
Развитие учебных навыков через применение наглядных пособий и перевода математических задач в практическую плоскость Соотношение величин
Соотношение величин Методы обработки данных и способы их представления в научном исследовании
Методы обработки данных и способы их представления в научном исследовании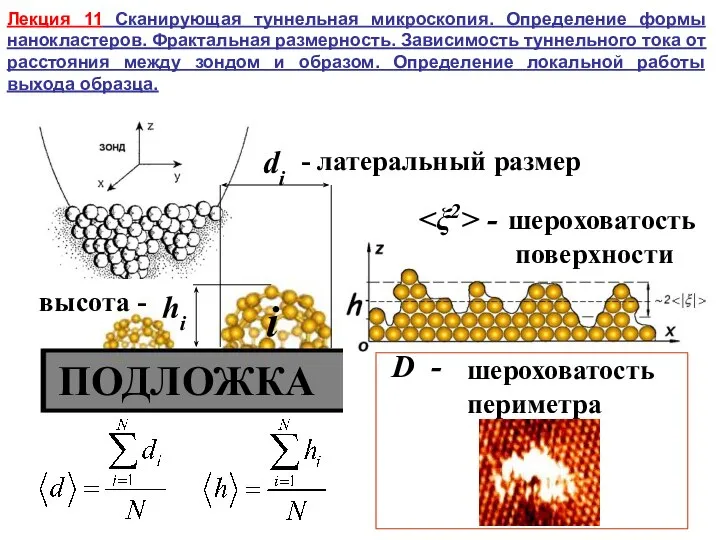 Сканирующая туннельная микроскопия. Определение формы нанокластеров. Фрактальная размерность
Сканирующая туннельная микроскопия. Определение формы нанокластеров. Фрактальная размерность Начальные сведения о задачах оптимизации
Начальные сведения о задачах оптимизации Юный математик
Юный математик Параллельные и перпендикулярные прямые
Параллельные и перпендикулярные прямые Первообразная. 11 класс
Первообразная. 11 класс Экстремум. Условный экстремум функции 2 переменных
Экстремум. Условный экстремум функции 2 переменных Кривые второго порядка
Кривые второго порядка Теорема Пифагора. Урок геометрии в 8 классе
Теорема Пифагора. Урок геометрии в 8 классе Презентация на тему Приёмы быстрого счета
Презентация на тему Приёмы быстрого счета  Презентация на тему Равнобедренный треугольник, признаки равенства треугольников
Презентация на тему Равнобедренный треугольник, признаки равенства треугольников  Разложение на множители с помощью формул
Разложение на множители с помощью формул Проектная деятельность на уроках математики. Задания для групповой работы (1-2 класс)
Проектная деятельность на уроках математики. Задания для групповой работы (1-2 класс) Неопределённый интеграл
Неопределённый интеграл Задачи на умножение
Задачи на умножение Прятки с фигурами
Прятки с фигурами Построение сечений
Построение сечений Основы матричной алгебры
Основы матричной алгебры Тригонометрические функции, их свойства и графики
Тригонометрические функции, их свойства и графики Деление и степень числа. Тест
Деление и степень числа. Тест Организация работы учителя с обучающимися, испытывающими трудности в обучении математике на уровне основного общего образования
Организация работы учителя с обучающимися, испытывающими трудности в обучении математике на уровне основного общего образования Закономерности между элементами фигуры и тенью при освещении параллельными лучами
Закономерности между элементами фигуры и тенью при освещении параллельными лучами Решение устных задач по готовым чертежам
Решение устных задач по готовым чертежам Элементы высшей математики. Свойства операции умножения
Элементы высшей математики. Свойства операции умножения Окружность и круг
Окружность и круг