Содержание
- 3. Содержанием работы является построение сечений по точкам, заданным на рёбрах многогранников: 2. Пирамиды 3. Призмы 1.
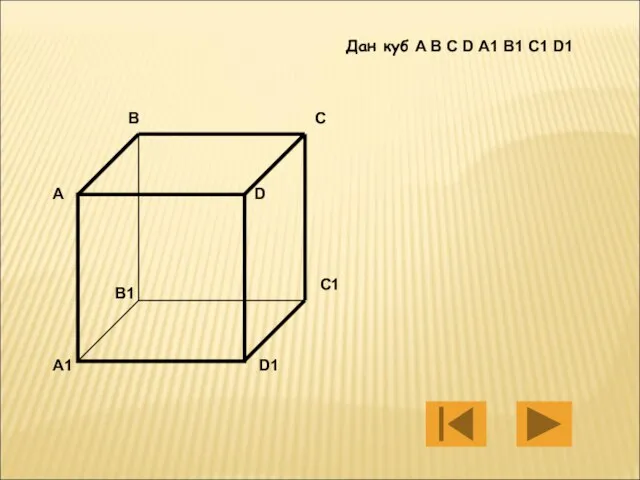
- 4. А В С D A1 B1 C1 D1 Дан куб A B C D A1 B1
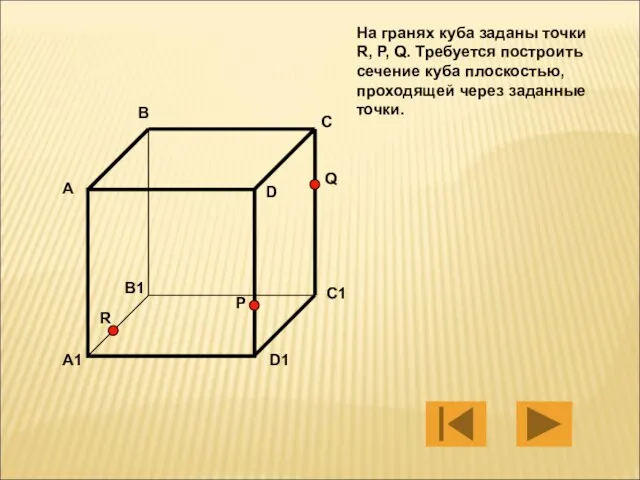
- 5. На гранях куба заданы точки R, P, Q. Требуется построить сечение куба плоскостью, проходящей через заданные
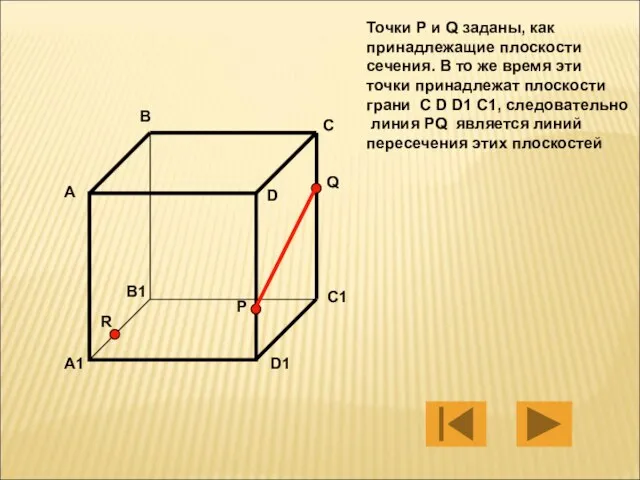
- 6. Точки Р и Q заданы, как принадлежащие плоскости сечения. В то же время эти точки принадлежат
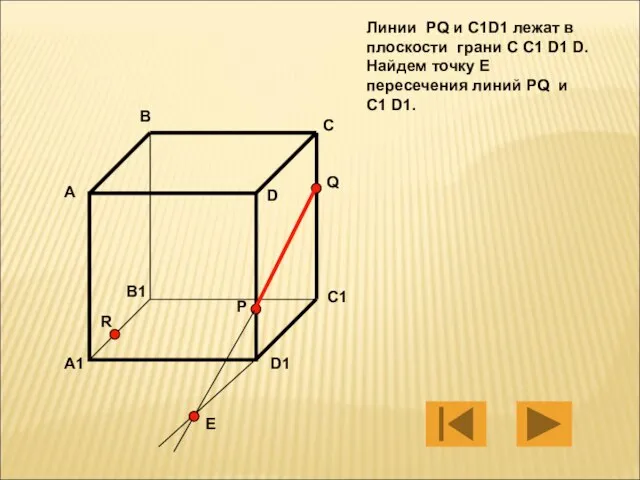
- 7. Линии PQ и C1D1 лежат в плоскости грани C C1 D1 D. Найдем точку Е пересечения
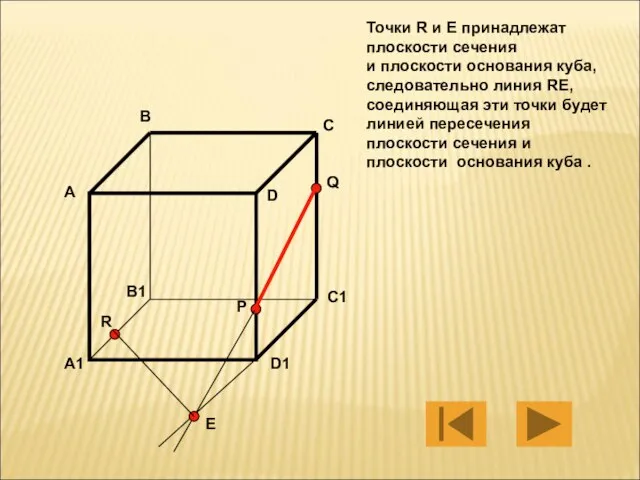
- 8. Точки R и E принадлежат плоскости сечения и плоскости основания куба, следовательно линия RE, соединяющая эти
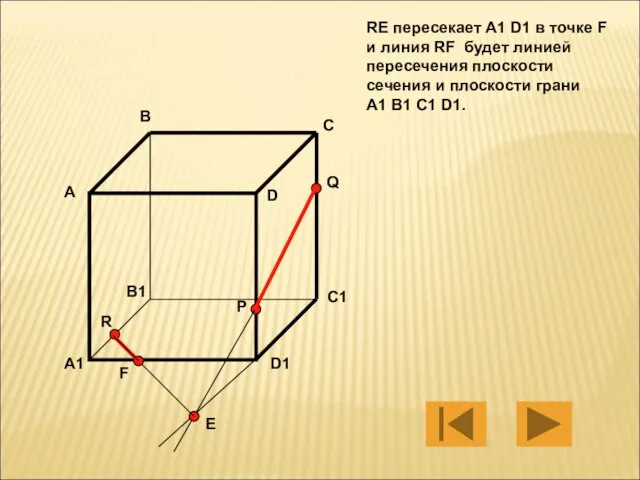
- 9. RE пересекает A1 D1 в точке F и линия RF будет линией пересечения плоскости сечения и
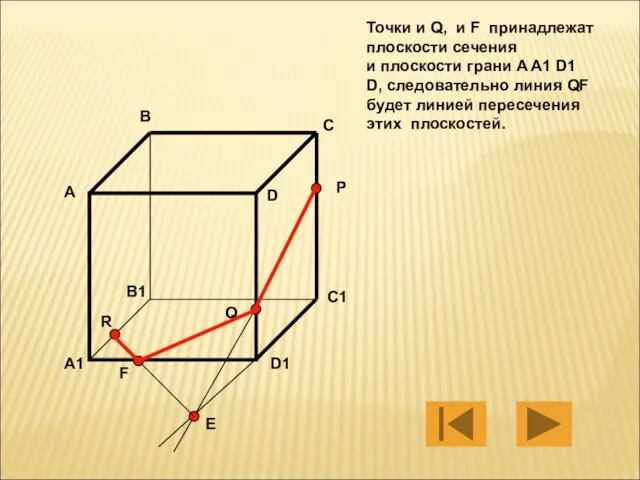
- 10. Точки и Q, и F принадлежат плоскости сечения и плоскости грани A A1 D1 D, следовательно
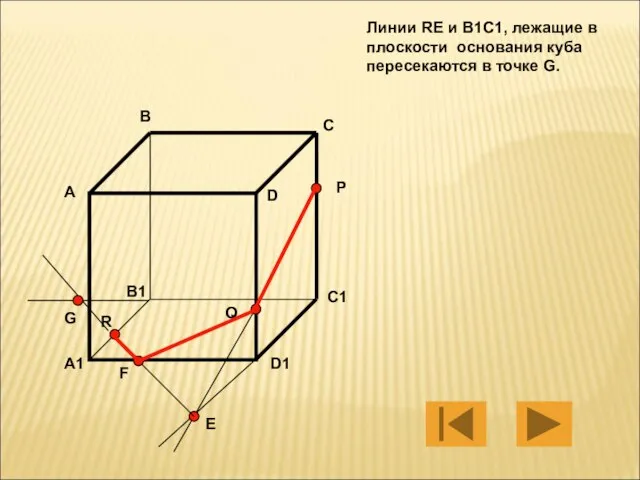
- 11. Линии RE и B1C1, лежащие в плоскости основания куба пересекаются в точке G. А В С
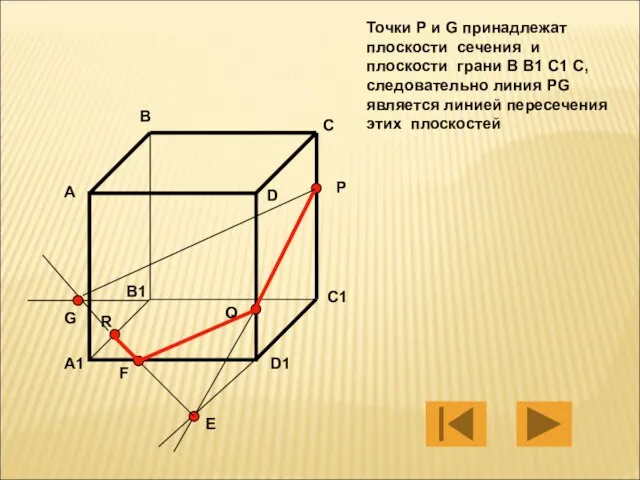
- 12. Точки P и G принадлежат плоскости сечения и плоскости грани B B1 C1 C, следовательно линия
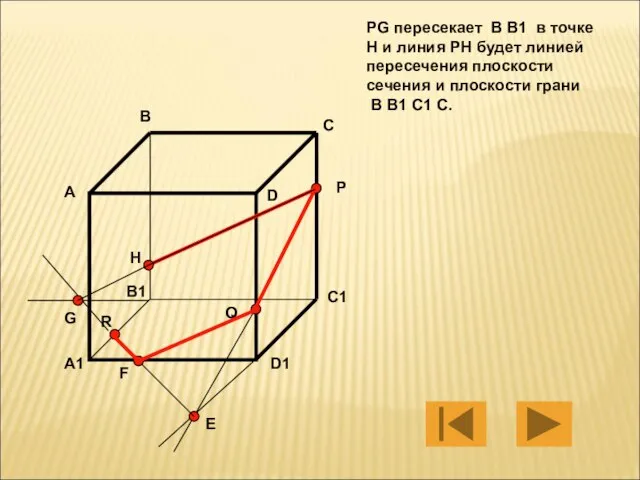
- 13. PG пересекает B B1 в точке H и линия PH будет линией пересечения плоскости сечения и
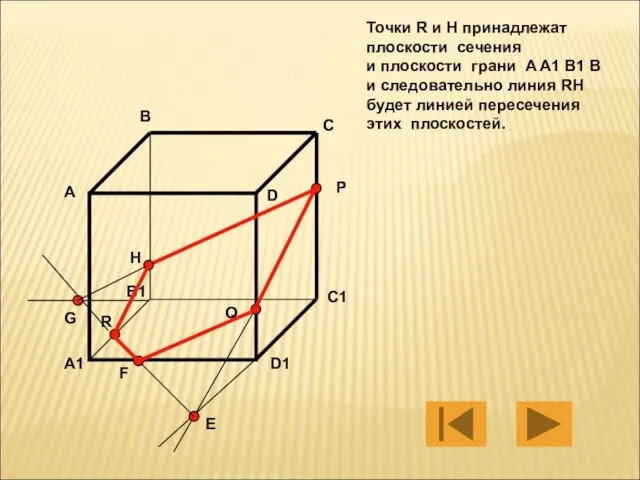
- 14. Точки R и H принадлежат плоскости сечения и плоскости грани A A1 B1 B и следовательно
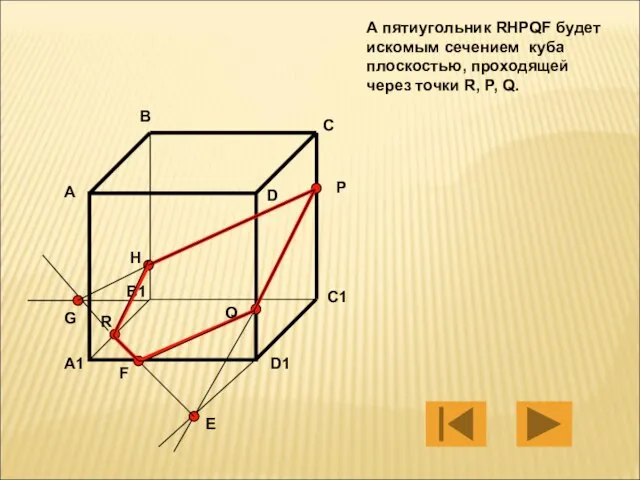
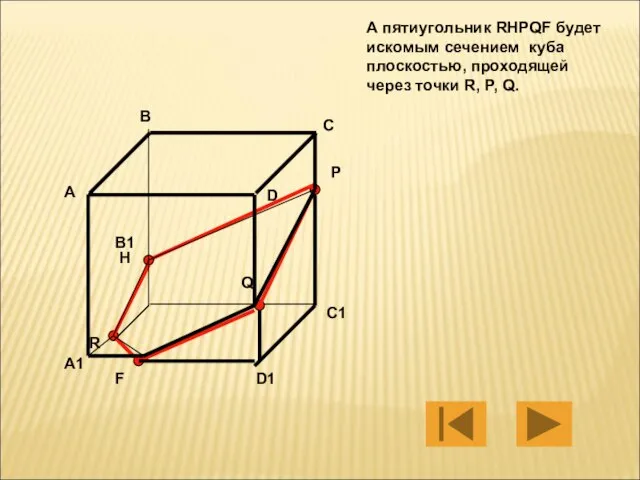
- 15. А пятиугольник RHPQF будет искомым сечением куба плоскостью, проходящей через точки R, P, Q. А В
- 16. А пятиугольник RHPQF будет искомым сечением куба плоскостью, проходящей через точки R, P, Q. А В
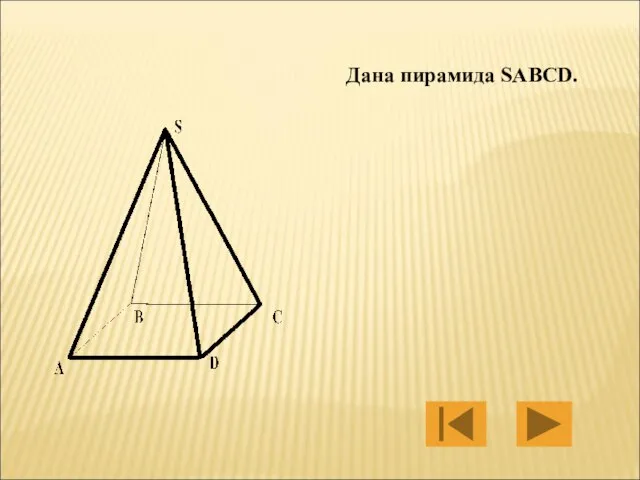
- 17. Дана пирамида SABCD.
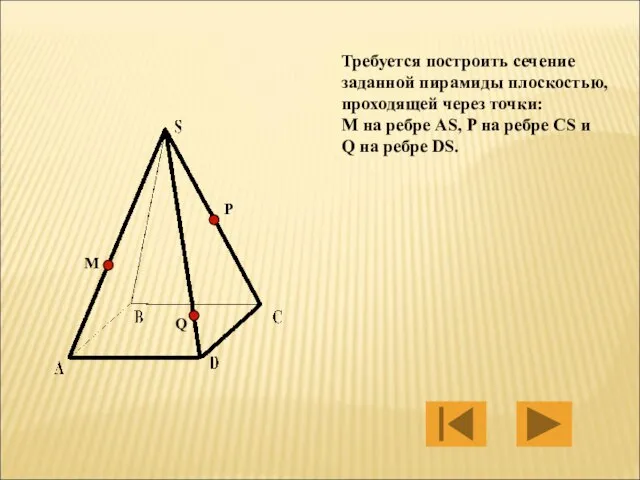
- 18. Требуется построить сечение заданной пирамиды плоскостью, проходящей через точки: М на ребре AS, P на ребре
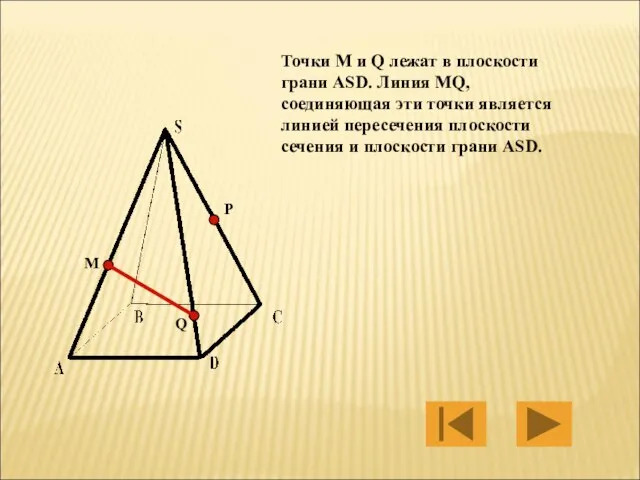
- 19. M P Q Точки M и Q лежат в плоскости грани АSD. Линия МQ, соединяющая эти
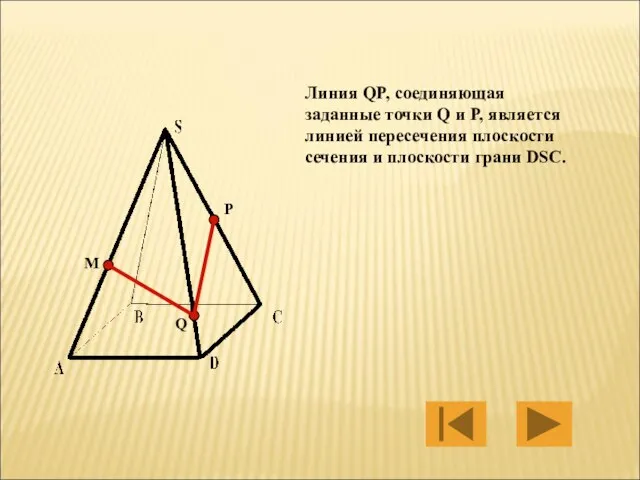
- 20. M P Q Линия QP, соединяющая заданные точки Q и P, является линией пересечения плоскости сечения
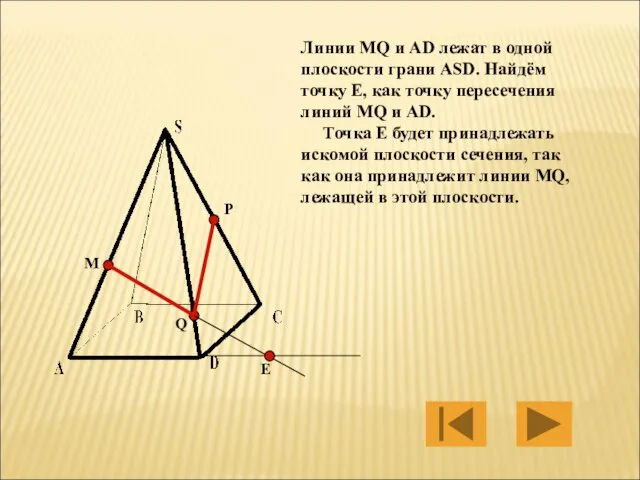
- 21. M P Q Линии MQ и AD лежат в одной плоскости грани ASD. Найдём точку Е,
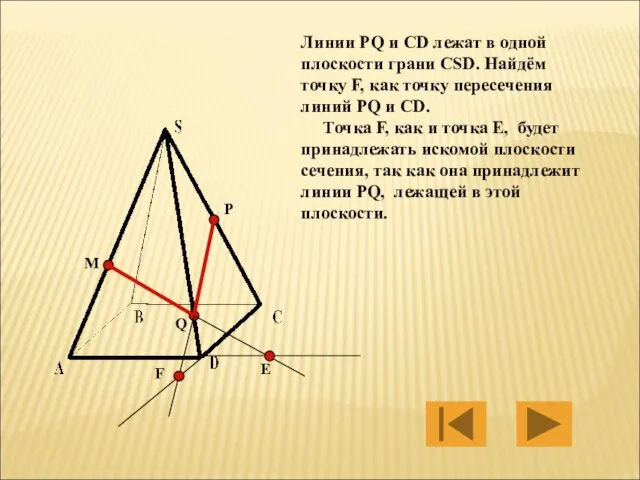
- 22. M P Q Е Линии PQ и CD лежат в одной плоскости грани CSD. Найдём точку
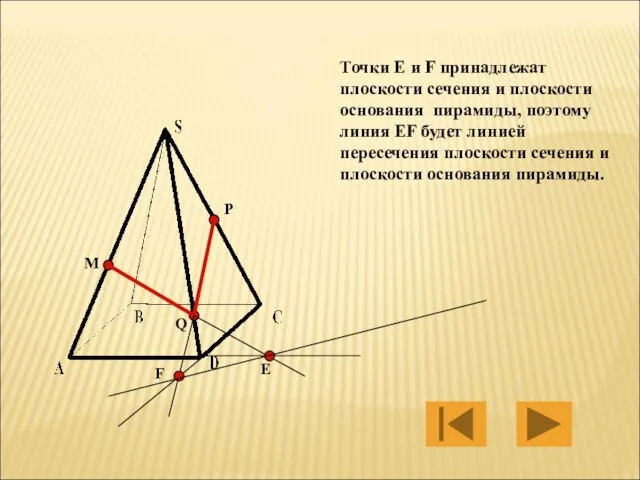
- 23. M P Q Е F Точки Е и F принадлежат плоскости сечения и плоскости основания пирамиды,
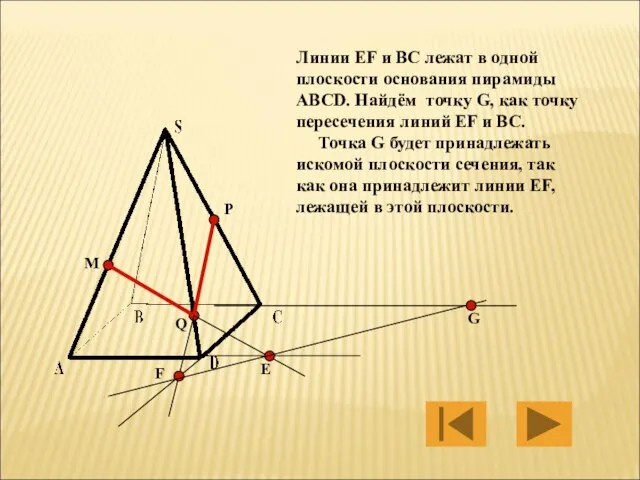
- 24. M P Q Е F Линии EF и BC лежат в одной плоскости основания пирамиды ABCD.
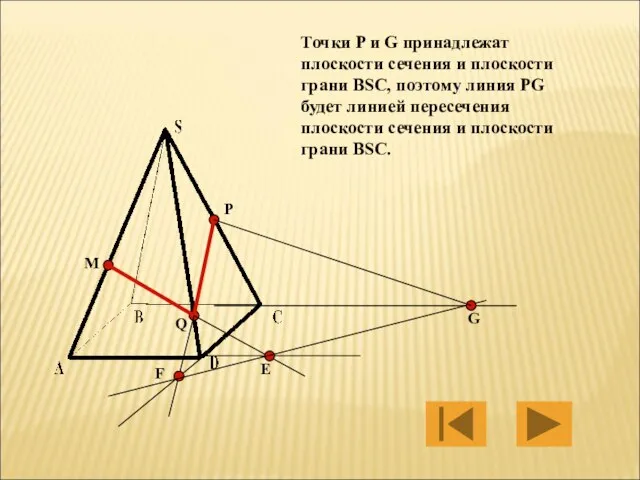
- 25. M P Q Е F G Точки P и G принадлежат плоскости сечения и плоскости грани
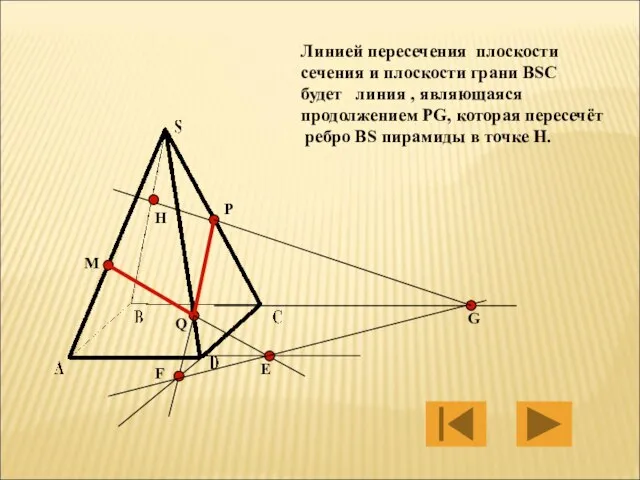
- 26. M P Q Е F G Линией пересечения плоскости сечения и плоскости грани BSC будет линия
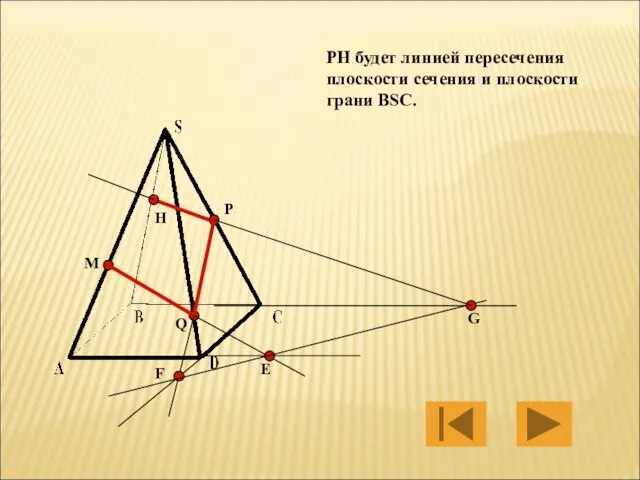
- 27. M P Q Е F G H PH будет линией пересечения плоскости сечения и плоскости грани
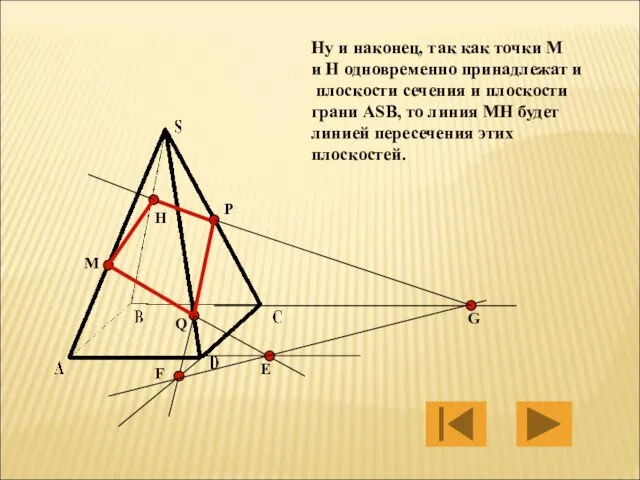
- 28. M P Q Е F G H Ну и наконец, так как точки M и H
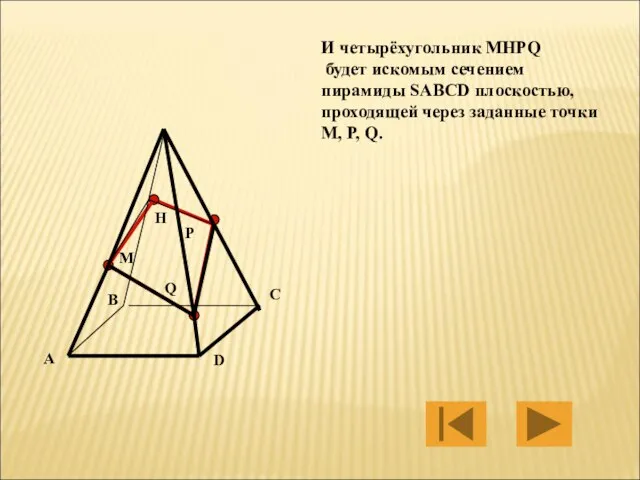
- 29. M P Q H И четырёхугольник MHPQ будет искомым сечением пирамиды SABCD плоскостью, проходящей через заданные
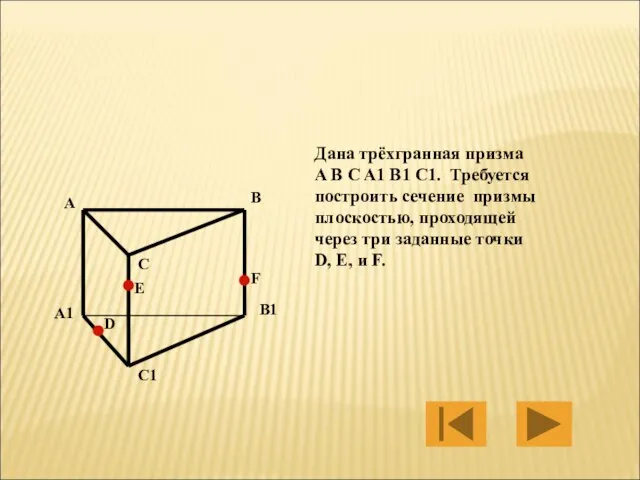
- 30. Дана трёхгранная призма A B C A1 B1 C1. Требуется построить сечение призмы плоскостью, проходящей через
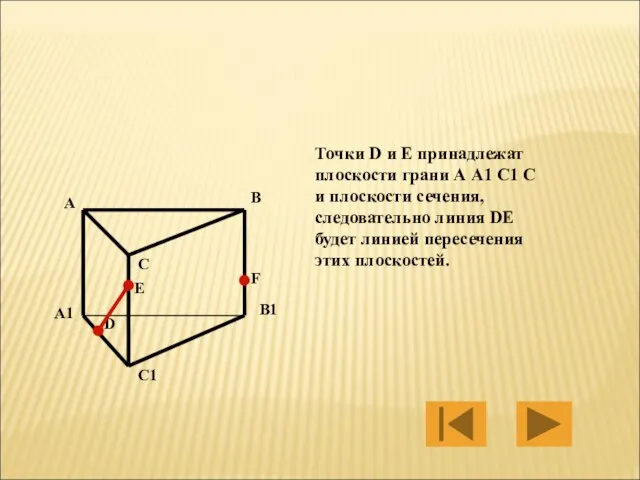
- 31. Точки D и E принадлежат плоскости грани А А1 С1 С и плоскости сечения, следовательно линия
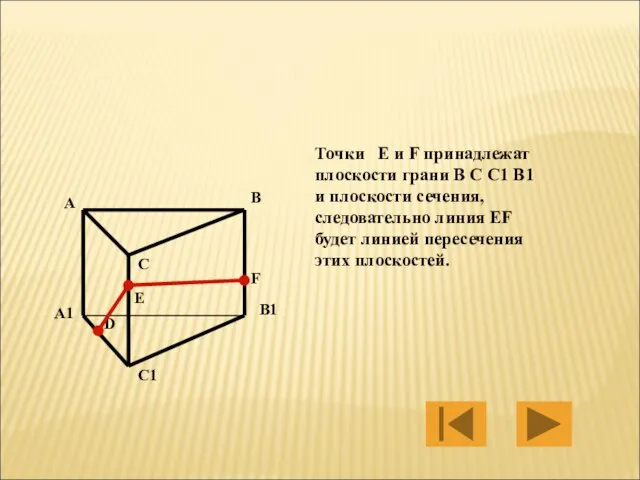
- 32. Точки E и F принадлежат плоскости грани B C C1 B1 и плоскости сечения, следовательно линия
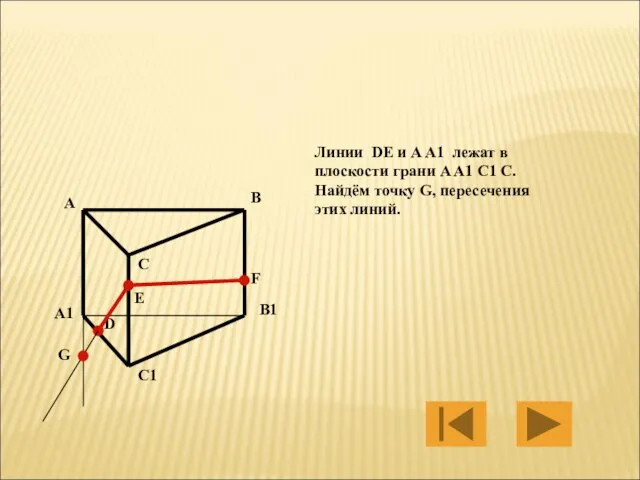
- 33. Линии DE и A A1 лежат в плоскости грани A A1 C1 C. Найдём точку G,
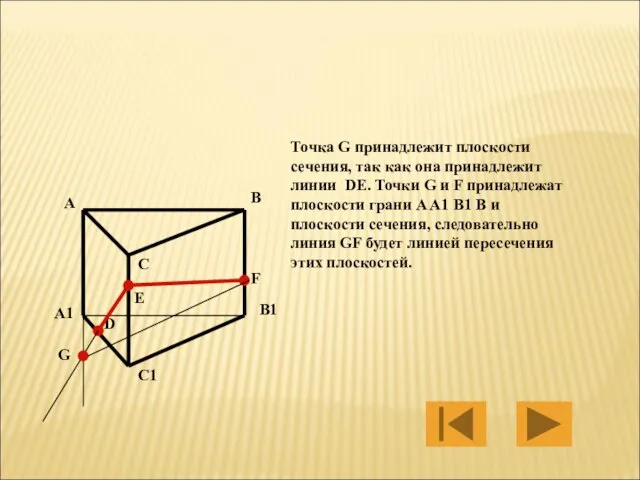
- 34. Точка G принадлежит плоскости сечения, так как она принадлежит линии DE. Точки G и F принадлежат
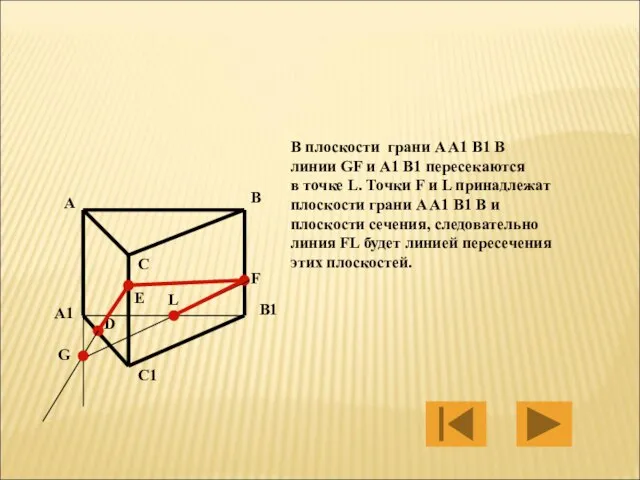
- 35. В плоскости грани A A1 B1 B линии GF и A1 B1 пересекаются в точке L.
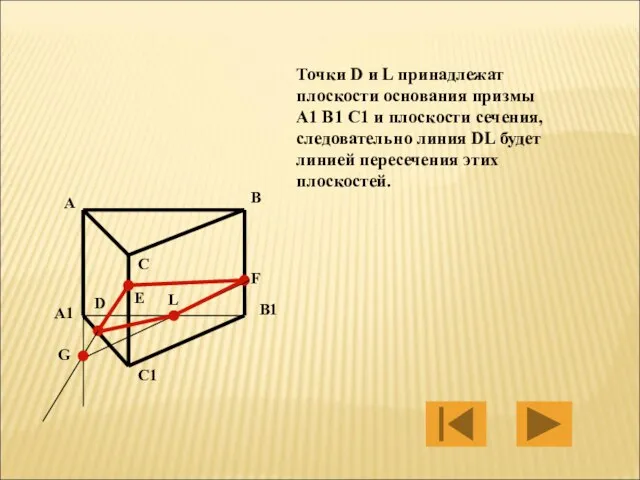
- 36. Точки D и L принадлежат плоскости основания призмы A1 B1 C1 и плоскости сечения, следовательно линия
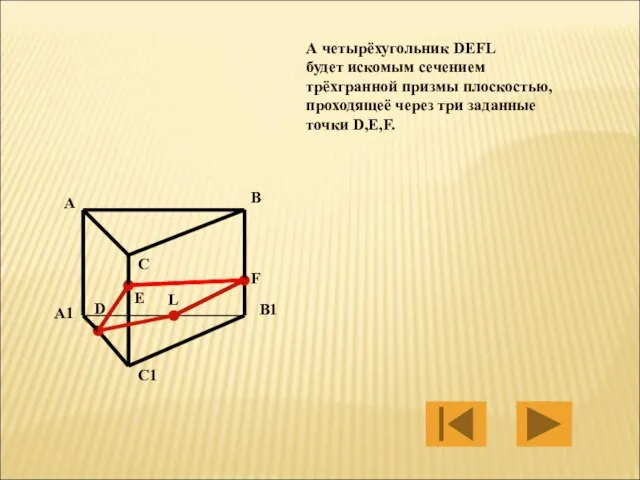
- 37. А четырёхугольник DEFL будет искомым сечением трёхгранной призмы плоскостью, проходящеё через три заданные точки D,E,F. A
- 41. Скачать презентацию



 Функция нескольких переменных
Функция нескольких переменных аксіоми стереометрії
аксіоми стереометрії Математический маятник. Измерения
Математический маятник. Измерения Сложение положительных и отрицательных чисел
Сложение положительных и отрицательных чисел Среднее арифметическое
Среднее арифметическое Обыкновенная дробь
Обыкновенная дробь Решение иррациональных уравнений
Решение иррациональных уравнений Дроби десятичные
Дроби десятичные Решение уравнений, содержащих параметры
Решение уравнений, содержащих параметры Предел функции
Предел функции Презентация на тему Основные тригонометрические формулы
Презентация на тему Основные тригонометрические формулы  Действия с многозначными числами
Действия с многозначными числами Линейные уравнения с одной переменной
Линейные уравнения с одной переменной Статические таблицы
Статические таблицы Площади четырехугольников
Площади четырехугольников Приёмы устных вычислений в пределах 1000
Приёмы устных вычислений в пределах 1000 Числительные. Количественные числительные
Числительные. Количественные числительные Свойства квадратных корней
Свойства квадратных корней Проценты. 5 класс
Проценты. 5 класс Копилка интересных идей и находок
Копилка интересных идей и находок Методика исследования понятия числа и его разрядной структуры, счетных операций
Методика исследования понятия числа и его разрядной структуры, счетных операций Умножение нуля и единицы
Умножение нуля и единицы Геометрия вокруг нас
Геометрия вокруг нас Характер и ритм линий как средство выражения
Характер и ритм линий как средство выражения Методы решения тригонометрических уравнений
Методы решения тригонометрических уравнений Определение.Модуль числа а
Определение.Модуль числа а Признаки равенства треугольников. Задачи на готовых чертежах
Признаки равенства треугольников. Задачи на готовых чертежах Скалярное произведение векторов. тест
Скалярное произведение векторов. тест