Построение сечений тетраэдра и параллелепипеда

Секущей плоскостью многогранника называется любая плоскость, по обе стороны от которой имеются точки данного многогранника.

Секущая плоскость пересекает грани многогранника по отрезкам. Многоугольник, сторонами которого являются эти отрезки, называется сечением многогранника.

Какие многоугольники могут получиться в сечении ?
Тетраэдр имеет 4 грани
В сечениях могут получиться:
Четырехугольники
Треугольники

Треугольники
Параллелепипед имеет 6 граней
Четырехугольники
Шестиугольники
Пятиугольники
В его сечениях
могут получиться:

При этом необходимо учитывать следующее:
1. Соединять можно только две точки, лежащие
в плоскости одной грани.
Для построения сечения нужно построить точки пересечения секущей плоскости с ребрами и соединить их отрезками.
2. Секущая плоскость пересекает параллельные грани по параллельным отрезкам.
3. Если в плоскости грани отмечена только одна точка, принадлежащая плоскости сечения, то надо построить дополнительную точку. Для этого необходимо найти точки пересечения уже построенных прямых с другими прямыми, лежащими в тех же гранях.

А
В
С
S
Задача 1. Построить сечение плоскостью, проходящей через данные точки D, Е, K.
D
E
K
M
F
Построение:
2. ЕК
3. ЕК ∩ АС = F
4. FD
5. FD ∩ BС = M
6. KM
1. DE
DЕKМ – искомое сечение

Задача 2. Построить сечение плоскостью, проходящей через точки Р, К, М, М∈ВС.
К
Р
М
Построение:
1. КP
2. EM ║ КP (К1Р1)
3. EK
KРNМE – искомое сечение
К1
Р1
E
N
4. МN ║ EK
5. РN

Пояснения к построению:
1. Соединяем точки K и F, принадлежащие одной плоскости А1В1С1D1.
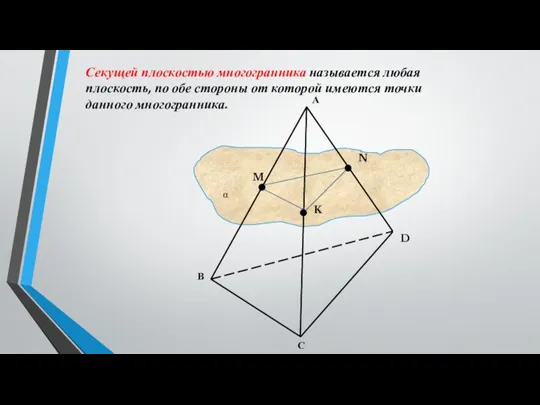
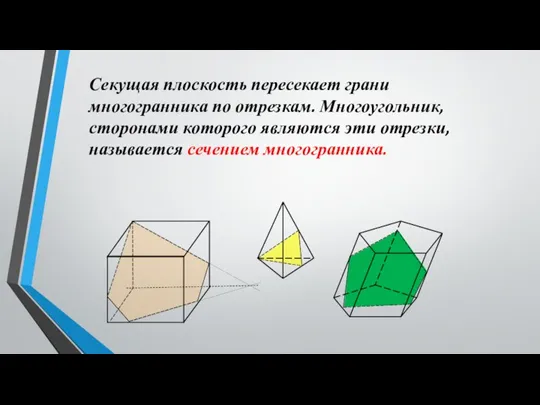
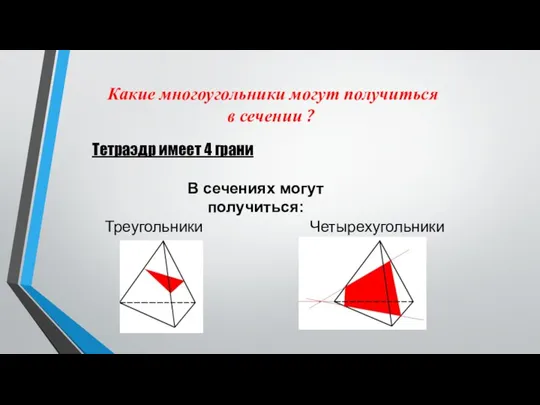
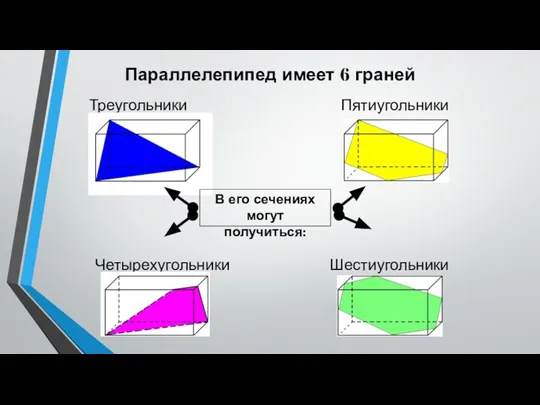
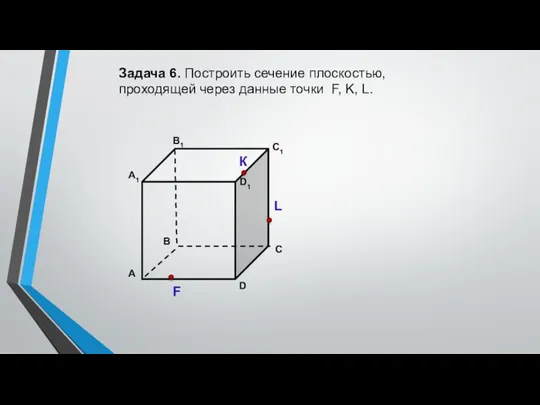
Задача 3. Построить сечение плоскостью, проходящей через данные точки Е, F, K.
К
L
М
Построение:
1. KF
2. FE
3. FE ∩ АB = L
EFKNM – искомое сечение
F
E
N
4. LN ║ FK
6. EM
5. LN ∩ AD = M
7. KN
Пояснения к построению:
2. Соединяем точки F и E, принадлежащие одной плоскости АА1В1В.
Пояснения к построению:
3. Прямые FE и АВ, лежащие в одной плоскости АА1В1В, пересекаются в точке L .
Пояснения к построению:
4. Проводим прямую LN параллельно FK (если секущая плоскость пересекает противоположные грани, то она пересекает их по параллельным отрезкам).
Пояснения к построению:
5. Прямая LN пересекает ребро AD в точке M.
Пояснения к построению:
6. Соединяем точки Е и М, принадлежащие одной плоскости АА1D1D.
Пояснения к построению:
7. Соединяем точки К и N, принадлежащие одной плоскости ВСС1В1.

А
В
С
S
Задача 4. Построить сечение плоскостью, проходящей через данные точки К, М, Р, Р∈АВС
К
М
Р
Е
N
F
Построение:
1. КМ
2. КМ ∩ СА = Е
3. EР
4. ЕР ∩ АВ = F
ЕР ∩ ВC = N
5. МF
6. NК
КМFN – искомое сечение

Задача 5. Построить сечение плоскостью, проходящей через точки К, L, М.
К
L
М
Построение:
1. ML
2. ML ∩ D1А1 = E
3. EK
МLFKPG – искомое сечение
F
E
N
P
G
T
4. EK ∩ А1B1 = F
6. LM ∩ D1D = N
5. LF
7. ЕK ∩ D1C1 = T
8. NT
9. NT ∩ DC = G
NT ∩ CC1 = P
10. MG
11. PK

Задача 6. Построить сечение плоскостью, проходящей через данные точки F, K, L.
К
L
F