Построение треугольника по трём элементам

Цель урока:
Познакомить со способами построения треугольника по трём элементам.
Развивать логическое и критическое мышление, способности к умственному эксперименту.
Воспитывать качества личности, обеспечивающие социальную мобильность, способность принимать самостоятельные решения.

«В геометрии нет царских путей!» - ответил Евклид царю Птолемею (3 век до н.э.)
В геометрии надо:
Знать
теорию (аксиомы, определения, теоремы).
Уметь
решать задачи, строить чертежи
Главное - думать!

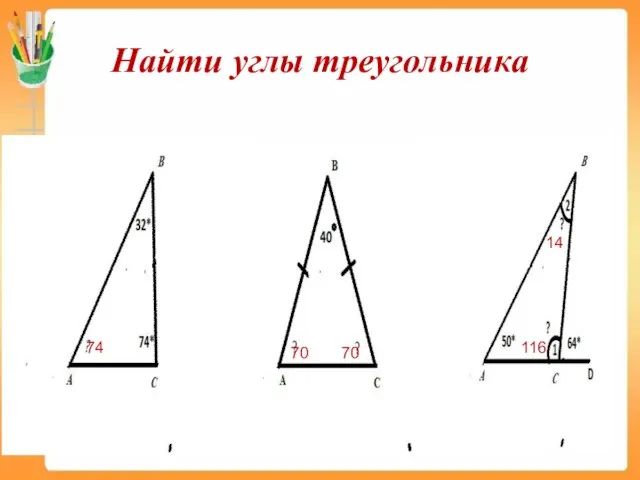
Найти углы треугольника
74
70
70
116
14

Выбрать верные и неверные утверждения
Неверно, «угол между ними».
Верно.
Неверно, в треугольнике только один тупой угол.
Верно, неравенство треугольника
Неверно, 1 + 2 < 4.

Выделить условие и заключение.
Записать в форме «Если …,то …».
Сформулировать обратное высказывание и противоположное высказывание.
«В равнобедренном треугольнике углы при основании равны»
«В прямоугольном треугольнике против угла в 30° лежит катет равный половине гипотенузы»
«Математику уже затем учить стоит, что она ум в порядок приводит» Ломоносов М.В.

Если треугольник равнобедренный, то углы при основании равны.
(свойство равнобедренного треугольника)
Если углы при основании равны, то треугольник равнобедренный.
(признак равнобедренного треугольника)

Если в прямоугольном треугольнике есть угол 30°, то катет против него равен половине гипотенузы.
Если в прямоугольном треугольнике катет равен половине гипотенузы, то угол против него 30°.
(свойства прямоугольного треугольника)

Если ты учишь математику, то твой ум в порядке.
Если твой ум в порядке, то ты учишь математику.
Если ты не учишь математику, то твой ум не в порядке.
(Закон математики)

Проблема
Как построить треугольник?

Построение треугольника
Анализ проблемы
Какие элементы и сколько нужно для построения?
Как связать эти элементы?
План построения.
Как это выполнить с помощью циркуля и линейки?

Вывод 1:Треугольник
можно построить по:
Двум сторонам и углу между ними
Стороне и двум прилежащим к ней углам
Трём сторонам

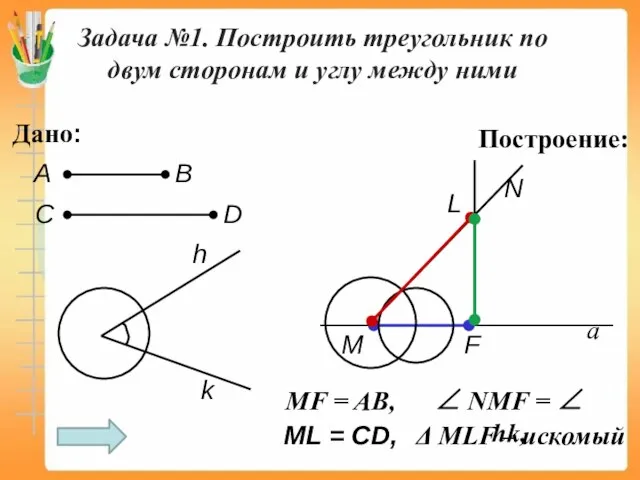
Задача №1. Построить треугольник по двум сторонам и углу между ними
Дано:
А
В
С
D
h
k
а
•
М
F
MF = AB,
L
∠ NMF = ∠ hk,
ML = CD,
Δ MLF – искомый
N
Построение:

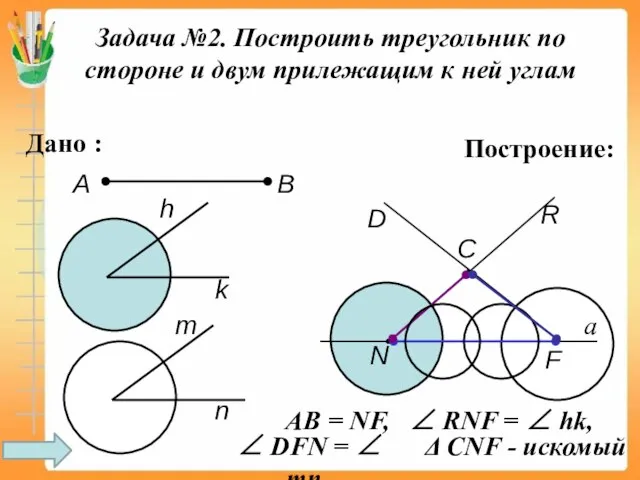
Задача №2. Построить треугольник по стороне и двум прилежащим к ней углам
Дано :
А
В
h
k
m
n
a
•
N
F
AB = NF,
R
∠ RNF = ∠ hk,
D
∠ DFN = ∠ mn,
•
C
Δ CNF - искомый
Построение:

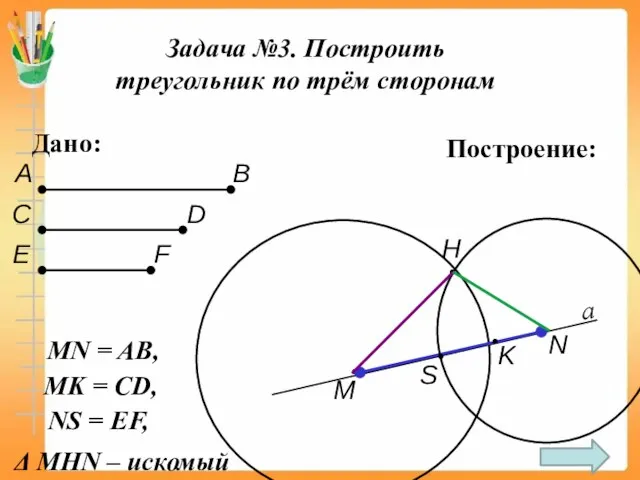
Задача №3. Построить треугольник по трём сторонам
Дано:
А
В
С
D
Е
F
а
•
М
N
MN = AB,
•
K
MK = CD,
•
S
NS = EF,
•
H
Δ MHN – искомый
Построение:

Вывод 2: схема, по которой обычно решают задачи на построение с помощью циркуля и линейки.
1. Отыскание способа решения задачи путём установления связей между искомыми элементами и данными задачи. Анализ дает возможность составить план решения задачи на построение.
2. Выполнение построения по намеченному плану.
3. Доказательство того, что построенная фигура удовлетворяет условиям задачи.
4. Исследование задачи, т.е. выяснение вопроса о том, при любых ли данных задача имеет решение, и если имеет, то сколько решений.

Оценивание границ своих знаний
Это мы изучили…
Это осталось за пределами …
Это мне помешает хорошо решать задачи…
Это пока не знает никто…

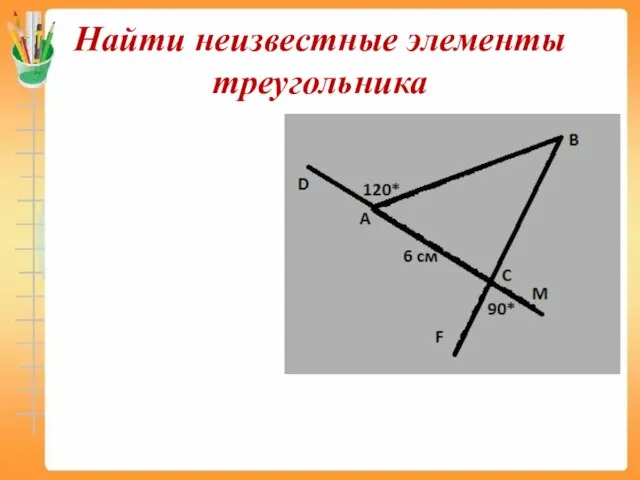
Найти неизвестные элементы треугольника

Домашнее задание.
Вопросы: 19,20 стр. 90.
№ 287, 289.