Знакочередующиеся и знакопеременные ряды

Знакочередующиеся ряды
Ряд называется знакочередующимся, если
любые два его соседних члена имеют разные знаки, то есть
или

Если члены знакочередующегося ряда убывают по
абсолютной величине и
то ряд сходится, а его сумма
не превосходит первого члена
Признак Лейбница

Пример 1.
1.
Все члены ряда убывают по абсолютной величине
2.
По признаку Лейбница ряд сходится

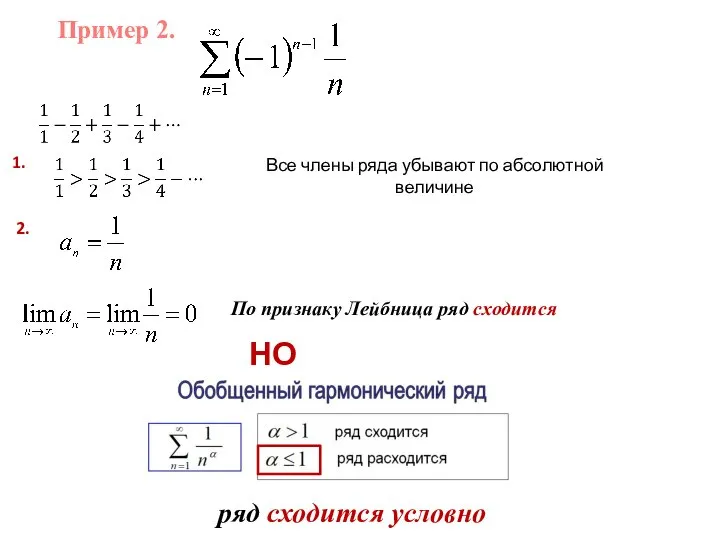
Пример 2.
1.
Все члены ряда убывают по абсолютной величине
2.
По признаку Лейбница ряд сходится
НО
ряд сходится условно

Пример 3.
1.
Все члены ряда убывают по абсолютной величине
2.
По признаку Лейбница ряд сходится
ряд сходится абсолютно
3.
Рассмотрим ходимость положительного ряда, используя признак Даламбера
Положительный ряд сходится по признаку Даламбера

Пример 4.
1.
Все члены ряда убывают по абсолютной величине
2.
По признаку Лейбница ряд сходится
ряд сходится абсолютно
3.
Рассмотрим ходимость положительного ряда, используя радикальный признак Коши сходимости
Положительный ряд сходится по радикальному признаку Коши

Знакопеременные ряды
Ряд называется знакопеременным,
если любые его члены могут быть как
положительными так и отрицательными.

Если ряд, составленный из абсолютных величин
членов данного ряда
сходится, то ряд сходится.
Достаточный признак сходимости

сходится по признаку Лейбница
Утверждение обратное достаточному признаку
сходимости неверно
расходится как гармонический ряд

Ряд называется абсолютно сходящимся, если
сходятся ряды и
Ряд называется условно сходящимся, если ряд - сходится, а ряд - расходится

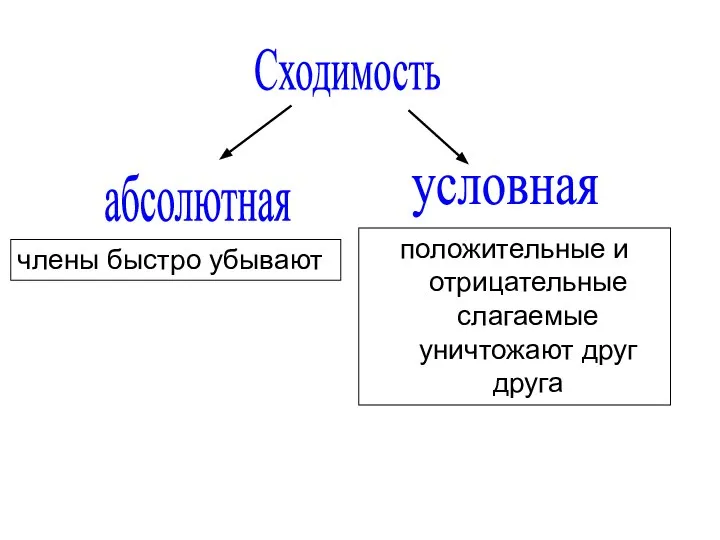
Сходимость
члены быстро убывают
абсолютная
условная
положительные и отрицательные слагаемые уничтожают друг друга

, так как
- сходится
- сходится
Сравним с рядом
Пример 1.
ряд сходится абсолютно

Пример 2.
1.
Все члены ряда убывают по абсолютной величине
2.
По признаку Лейбница ряд расходится

Пример 3.
ряд сходится абсолютно
Рассмотрим ходимость положительного ряда, используя признак Даламбера
Положительный ряд сходится по признаку Даламбера

Пример 4.
ряд сходится абсолютно
Рассмотрим ходимость положительного ряда, используя радикальный признак Коши
Положительный ряд сходится по признаку Коши