Содержание
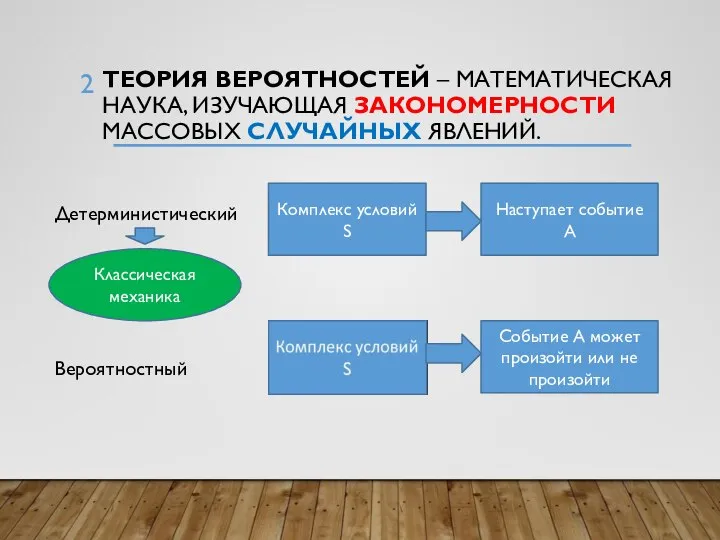
- 2. ТЕОРИЯ ВЕРОЯТНОСТЕЙ – МАТЕМАТИЧЕСКАЯ НАУКА, ИЗУЧАЮЩАЯ ЗАКОНОМЕРНОСТИ МАССОВЫХ СЛУЧАЙНЫХ ЯВЛЕНИЙ. Детерминистический Вероятностный Комплекс условий S Наступает
- 3. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ Предмет изучения ТВ – модели случайных экспериментов. Случайный эксперимент: исход нельзя однозначно определить условиями
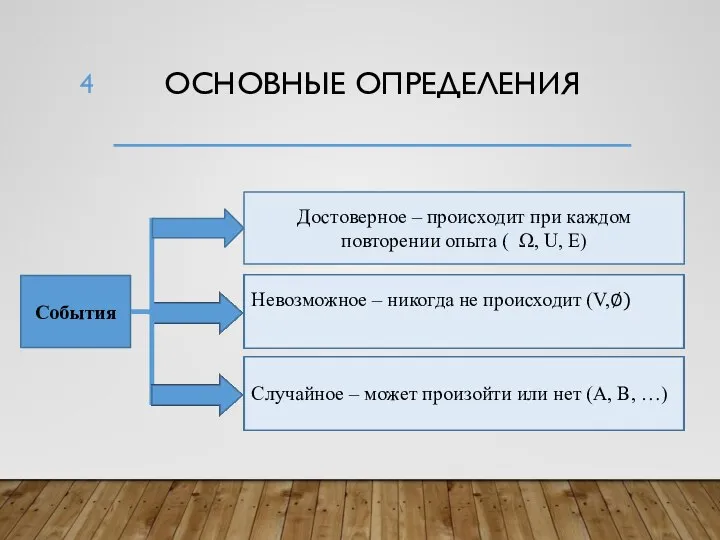
- 4. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ События Достоверное – происходит при каждом повторении опыта ( Ω, U, E) Невозможное –
- 5. ВЕРОЯТНОСТЬ СОБЫТИЙ
- 6. ВЕРОЯТНОСТЬ СОБЫТИЙ Колода карт (52 карты) раздается на четырех игроков. Найти вероятность того, что данный игрок
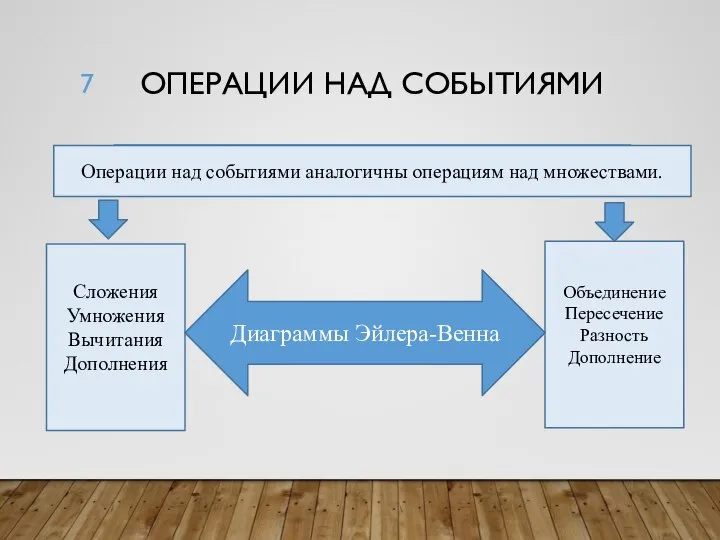
- 7. ОПЕРАЦИИ НАД СОБЫТИЯМИ Операции над событиями аналогичны операциям над множествами. Сложения Умножения Вычитания Дополнения Объединение Пересечение
- 8. Условная вероятность. Независимые события
- 9. ФОРМУЛА УМНОЖЕНИЯ ВЕРОЯТНОСТЕЙ Ω Р(А· В) = Р(А)· Р(В) Вероятность совместного появления двух зависимых событий равна
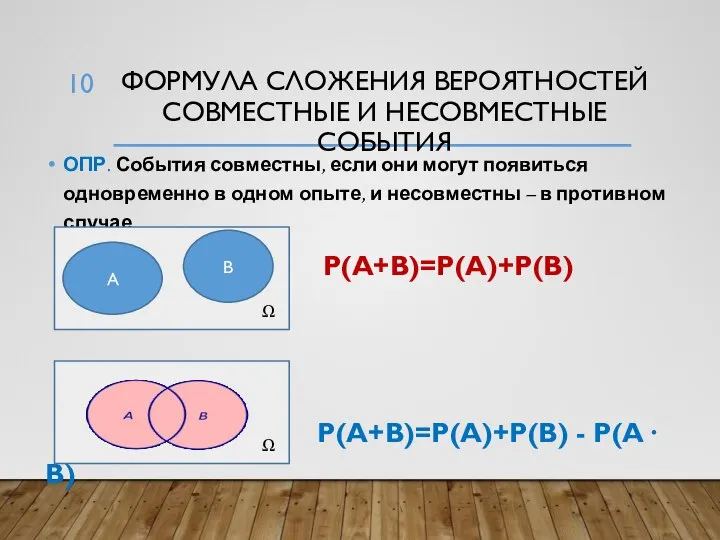
- 10. ФОРМУЛА СЛОЖЕНИЯ ВЕРОЯТНОСТЕЙ СОВМЕСТНЫЕ И НЕСОВМЕСТНЫЕ СОБЫТИЯ ОПР. События совместны, если они могут появиться одновременно в
- 11. ПРОТИВОПОЛОЖНОЕ СОБЫТИЕ
- 13. Скачать презентацию






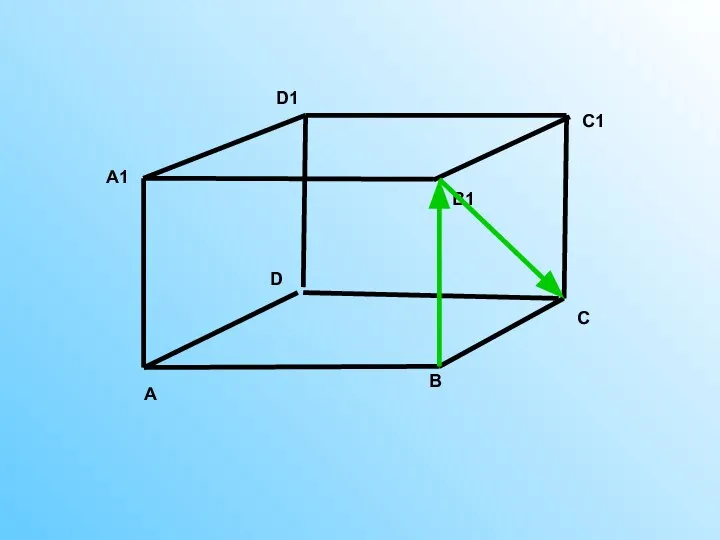 Угол между векторами
Угол между векторами Алгоритмическое и программное обеспечение для решения задач обработки статистической информации
Алгоритмическое и программное обеспечение для решения задач обработки статистической информации Умножение и деление десятичных дробей. Самостоятельная работа
Умножение и деление десятичных дробей. Самостоятельная работа Графики кусочных функций
Графики кусочных функций Параллельный перенос
Параллельный перенос Функция y=sin x, её свойства и график
Функция y=sin x, её свойства и график Решение квадратных неравенств
Решение квадратных неравенств Презентация на тему День числа П
Презентация на тему День числа П  Многогранники, 10 класс
Многогранники, 10 класс Багдадская математическая школа
Багдадская математическая школа Число и цифра 2
Число и цифра 2 Шарады, метаграммы, логогрифы
Шарады, метаграммы, логогрифы Основное свойство первообразной
Основное свойство первообразной Раздел 3. Линейная алгебра с элементами аналитической геометрии
Раздел 3. Линейная алгебра с элементами аналитической геометрии В мире рациональных уравнений
В мире рациональных уравнений ризнаки монотонности функции. Экстремум функции. Исследование функции на монотонность и экстремум
ризнаки монотонности функции. Экстремум функции. Исследование функции на монотонность и экстремум Прямое + ; - 2 Д
Прямое + ; - 2 Д Integrarea prin părți
Integrarea prin părți Теорема косинусов
Теорема косинусов Урок математики в 1 классе
Урок математики в 1 классе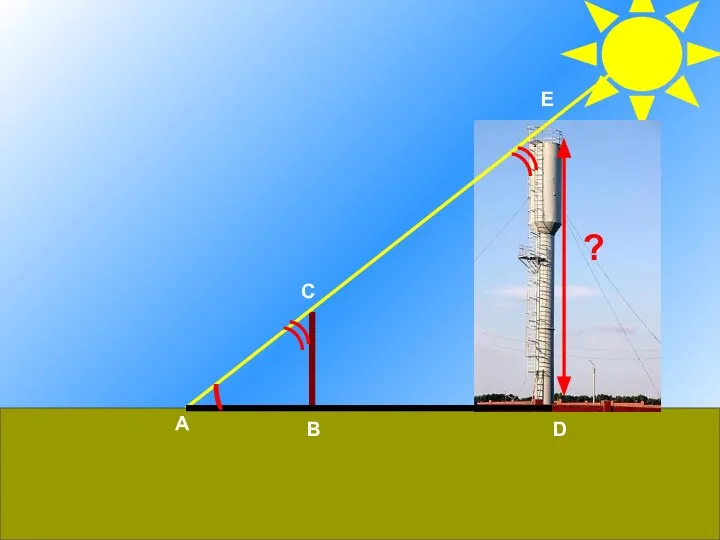 Решение задач на применение признаков подобия треугольников
Решение задач на применение признаков подобия треугольников Действия над алгебраическими дробями. 7 класс
Действия над алгебраическими дробями. 7 класс Задачки со всего света. Проект Секреты чисел. Команда Искорка
Задачки со всего света. Проект Секреты чисел. Команда Искорка Презентация на тему Неполные квадратные уравнения
Презентация на тему Неполные квадратные уравнения  Натуральные числа. Обобщающий урок
Натуральные числа. Обобщающий урок Множество. Сравнение множеств
Множество. Сравнение множеств Заочное путешествие на необитаемый остров
Заочное путешествие на необитаемый остров Круг, окружность, длина и площадь окружности
Круг, окружность, длина и площадь окружности