Поверхности второго порядка

История
Ученые, внесшие особый вклад в развитие теории поверхностей второго порядка
Гаспар Монж, 1749-1818
Леонард Эйлер, 1707-1783

Поверхность второго порядка
− геометрическое место точек трёхмерного пространства,
прямоугольные координаты которых удовлетворяют
уравнению вида

Уравнение может определять относительно OXYZ вырожденную поверхность (пару плоскостей, точку, пустое множество и т.д.)
Если поверхность невырожденная, то ее уравнение может быть приведено к каноническому виду

Классификация уравнений поверхностей второго порядка

Эллипсоид
ellipsoid(0,0,0,2,8,5)
[X,Y,Z] = sphere(20);
surf(X,Y,Z)
r = 5;
X2 = X * r;
Y2 = Y * r;
Z2 = Z * r;
surf(X2+5,Y2-5,Z2)
[X,Y,Z] = ellipsoid(x0,y0,z0,xr,yr,zr)
[X,Y,Z] = sphere(N),
N – количество граней

Гиперболоид
однополостный
[X,Y,Z] = meshgrid(-10:0.3:10,-10:0.3:10,-10:0.3:10);
a=1;b=1;c=1;
V = (X.^2)./(a^2) + (Y.^2)./(b^2) - (Z.^2)/(c^2);
p=patch(isosurface(X,Y,Z,V,5));
set(p,'FaceColor','red','EdgeColor','none');
view(3);
grid on
camlight
patch(X,Y,Z,C) создает полигоны в трехмерных координатах с помощью X,Y, и Z
Трехмерный массив - объемные данные

Гиперболоид
двуполостный
[X,Y,Z] = meshgrid(-10:0.3:10,-10:0.3:10,-10:0.3:10);
a=1;b=1;c=1;
V = (X.^2)./(a^2) + (Y.^2)./(b^2) - (Z.^2)/(c^2);
p=patch(isosurface(X,Y,Z,-V,1));
set(p,'FaceColor’, 'red’, 'EdgeColor','none');
view(3);
grid on
camlight

Конус
второго порядка
t = [-0.3;0.3];
[X,Y,Z] = cylinder(t,100);
s=surf(X,Y,Z);
alpha(.2)
axis equal

Параболоид
эллиптический
a=16;
b=16;
[X,Y]=meshgrid(-a:0.1:a,-b:0.1:b);
Z=(X.^2/a^2 +Y.^2/b^2 );
mesh(X,Y,Z);
xlabel('x'), ylabel('y'),zlabel('z')
colormap(pink)
colorbar

Параболоид
гиперболический
a=16;b=16;
[X,Y]=meshgrid(-a:0.1:a,-b:0.1:b);
Z=(X.^2/a^2 -Y.^2/b^2 );
mesh(X,Y,Z)
xlabel('x'),ylabel('y'),zlabel('z')
colormap(pink)
colorbar

Пара пересекающихся плоскостей
[X,Y,Z] = meshgrid(-10:0.3:10,-10:0.3:10,-10:0.3:10);
a=1;b=1;
V = (X.^2)./(a^2) - (Y.^2)./(b^2) - Z.*0;
p=patch(isosurface(X,Y,Z,V,0));
set(p,'FaceColor','red','EdgeColor','none’);
view(3);
axis equal
camlight

Цилиндр
гиперболический
[X,Y,Z] = meshgrid(-10:0.3:10,-10:0.3:10,-10:0.3:10);
a=1;b=1;
V = (X.^2)./(a^2) - (Y.^2)./(b^2) - 1;
p=patch(isosurface(X,Y,Z,V,0));
set(p,'FaceColor','red','EdgeColor','none');
view(3);
grid on
camlight

Цилиндр
эллиптический
[X,Y,Z] = cylinder(6,50);
C=X.*(Z-5);
surf(X,Y,Z,C)
[X,Y,Z] = cylinder(R,N), N – количество граней

Цилиндр
гиперболический
[X,Y,Z] = meshgrid(-10:0.3:10,-10:0.3:10,-10:0.3:10);
a=1;b=1;
V = (X.^2)./(a^2) + (Y.^2)./(b^2) - Z.*1;
p=patch(isosurface(X,Y,Z,V,0));
set(p,'FaceColor','red','EdgeColor','none');
view(3);
grid on
camlight

Цилиндр
параболический
[X,Y,Z] = meshgrid(-20:0.5:20,-20:0.5:20,-20:0.5:20);
p=2;
V = Y.^2-2*p*X;
p=patch(isosurface(X,Y,Z,V,1));
set(p,'FaceColor','m','EdgeColor','none');
view(3);
axis equal, grid on
camlight

Функции для участков поверхностей и сеток

surfс()
[X,Y]=meshgrid([-3:0.1:3]);
Z=sin(X)./(X.^2+Y.^2+0.3);
surfc(X,Y,Z)
– дополнительное построение контурного графика проекции фигуры на опорную плоскость.

[X,Y]=meshgrid([-3:0.1:3]);
Z=sin(X)./(X.^2+Y.^2+0.3);
surfl(X,Y,Z)
colormap(cool)
shading interp
colorbar
- имитирует оптические эффекты рассеивания, отражения и зеркального отражения света
surfl()

contour3(peaks,20)
colormap(pink)
[x,y]=meshgrid(-3:0.1:3);
z=x.^2+y.^2;
contour3 (x,y,z,40)
colormap (bone)
colorbar
contour3()

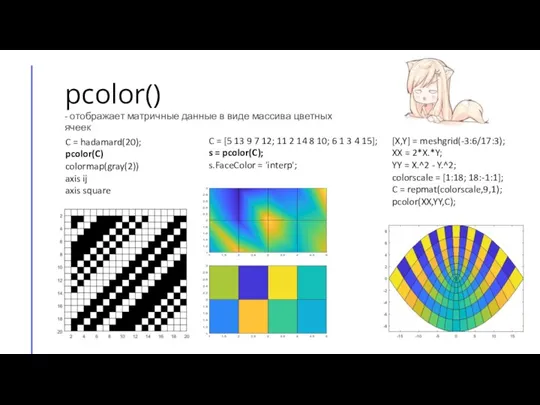
pcolor()
- отображает матричные данные в виде массива цветных ячеек
C = hadamard(20);
pcolor(C)
colormap(gray(2))
axis ij
axis square
C = [5 13 9 7 12; 11 2 14 8 10; 6 1 3 4 15];
s = pcolor(C);
s.FaceColor = 'interp';
[X,Y] = meshgrid(-3:6/17:3);
XX = 2*X.*Y;
YY = X.^2 - Y.^2;
colorscale = [1:18; 18:-1:1];
C = repmat(colorscale,9,1);
pcolor(XX,YY,C);

ПРИМЕНЕНИЕ

АРХИТЕКТУРА

Гиперболические конструкции
Первая гиперболическая башня, Нижний Новгород, 1896
Преимущества
Жесткая конструкция
Не страдает от ветровой нагрузки из-за своей решетчатой конструкции
«Соумайя» — музей искусства в Мехико, Мексика, 1994 год
Пример однополостного гиперболоида
Мост Мира, Тбилиси, 2010 год,
Гиперболический параболоид

«Хан Шатыр», Казахстан, 2010 год
Совокупность парабол
«Яйцо», Индия, 2010 год
Эллипсоид

Мачты
В начале 20-го века многие боевые корабли в США, строились с ажурными гиперболоидными мачтами.

БИОЛОГИЯ

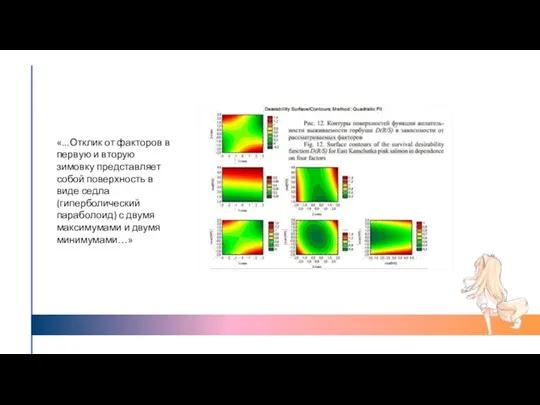
Поверхность отклика выживаемости
Из аннотации:
«…Зависимости выживаемости горбуши (R/S - количество потомков на производителя) от факторов внешней среды имеют нелинейный характер и описываются уравнением параболы. На основании таких взаимодействий строятся модели выживаемости горбуши.
Основной метод моделирования - общая модель, где отклики выживаемости представляются как поверхности 2-го порядка. Полученные модели с высокой точностью описывают флюктуации наблюдаемых значений R/S…»
Отрывок из статьи

«...Отклик от факторов в первую и вторую зимовку представляет собой поверхность в виде седла (гиперболический параболоид) с двумя максимумами и двумя минимумами…»

Причины резкого снижения численности горбуши

ФИЗИКА

Проектирование зеркальных и зеркально-оптических систем
Теорема. Отражающие поверхности второго порядка (параболоидальная, эллипсоидальная и гиперболоидальная) характеризуются следующими свойствами:

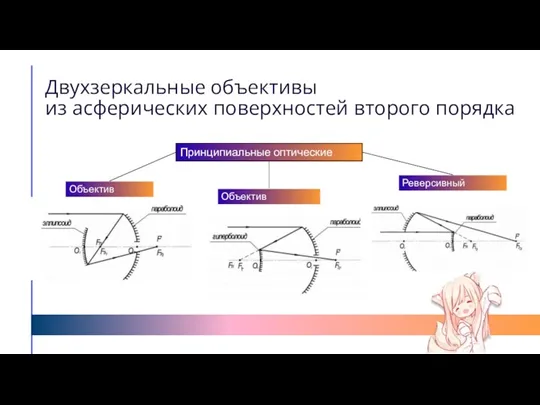
Двухзеркальные объективы
из асферических поверхностей второго порядка
Объектив Грегори
Объектив Кассегрена
Реверсивный объектив
Принципиальные оптические схемы

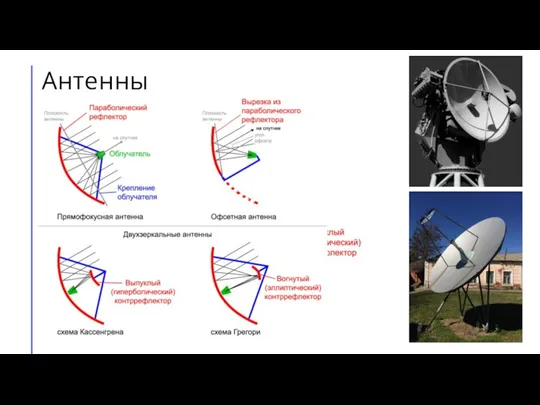
Антенны
Антенна Кассегрена: основное параболическое зеркало и гиперболическое вспомогательное зеркало.
Преимущества: небольшие размеры и значительные допуски по размещению излучателя, что способствует появлению разнообразных конструкций антенн

ХИМИЯ
кристаллография

Поверхности 2 порядка как характеристика кристалла и его свойств

Волновая поверхность двуосного кристалла
Волновая поверхность — поверхность скоростей распространения света в кристалле или «геометрическое место точек, колеблющихся в одинаковой фазе».
Кристаллы низшей категории – двухосные
Их волновая поверхность состоит из частично пересекающихся сфер и эллипсоидов

ВЫВОДЫ
Теория поверхностей второго порядка находит свое применение во многих областях науки и жизни.
Интерес к ней вряд ли когда-нибудь будет исчерпан.

Источники
https://yandex.ru/collections/api/links/redirect/?url=https%3A%2F%2Fcyberleninka.ru%2Farticle%2Fn%2Faberratsionnye-svoystva-otrazhayuschih-poverhnostey-vtorogo-poryadka%2Fviewer&yid=14401811598899858 - «Аберрационные свойства отражающих поверхностей второго порядка» Андреев Л.Н., Комарова Ю.А.
https://cyberleninka.ru/article/n/vyzhivaemost-kamchatskoy-gorbushi-kak-rezultat-sovokupnogo-vozdeystviya-plotnostnoy-regulyatsii-i-vneshnih-faktorov-sredy - «Выживаемость камчатской горбуши как результат совокупного воздействия плотностной регуляции и внешних факторов среды», Фельдман М.Г., Шевляков Е.А.
https://ru.wikipedia.org
https://cyberleninka.ru – все научные статьи взяты отсюда
https://zen.yandex.ru/media/marin/russkie-machty-amerikanskih-linkorov-5d81fc141e8e3f00ae70f14e - фото военных кораблей разных стран 20 века в цвете
https://www.mathworks.com – теория по матлабу
https://e-koncept.ru/2015/65340.htm - Шкода Ю. И. «Кривые и поверхности второго порядка в архитектуре» // Научно-методический электронный журнал «Концепт»
«Кристаллофизика» // Семенова О.Р.
https://studopedia.ru/4_126336_funktsiya-otklika-faktori-parametri-i-trebovaniya-k-nim.html - «Функция отклика. Факторы, параметры и требования к ним»
https://zen.yandex.ru/media/marin/russkie-machty-amerikanskih-linkorov-5d81fc141e8e3f00ae70f14e - Русские мачты американских лиинкоров