Содержание
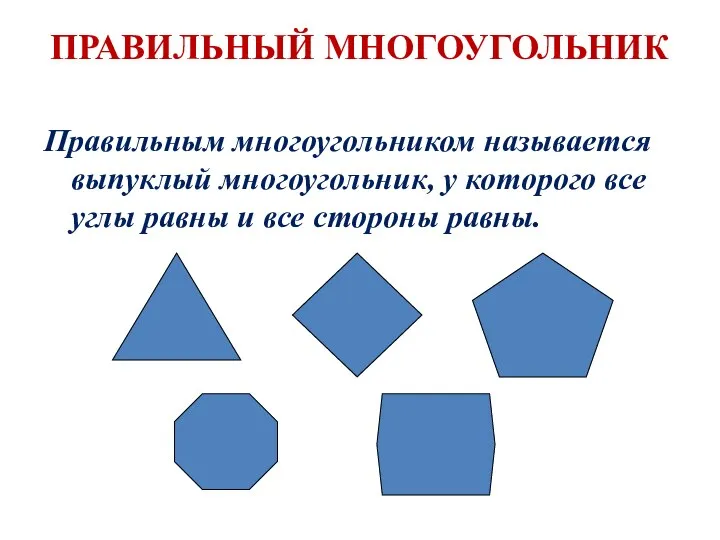
- 2. ПРАВИЛЬНЫЙ МНОГОУГОЛЬНИК Правильным многоугольником называется выпуклый многоугольник, у которого все углы равны и все стороны равны.
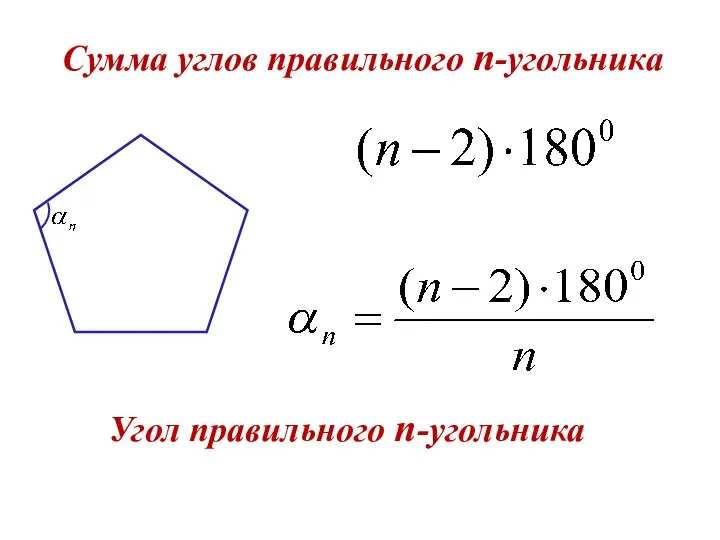
- 3. Сумма углов правильного n-угольника Угол правильного n-угольника
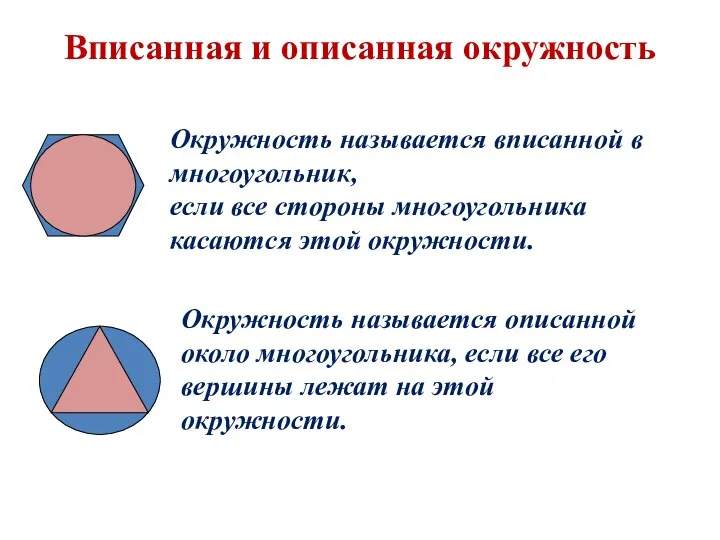
- 4. Вписанная и описанная окружность Окружность называется вписанной в многоугольник, если все стороны многоугольника касаются этой окружности.
- 5. Окружность, вписанная в правильный многоугольник, касается сторон многоугольника в их серединах. Центр окружности, описанной около правильного
- 6. ФОРМУЛЫ ДЛЯ ВЫЧИСЛЕНИЯ Площадь правильного многоугольника Сторона правильного многоугольника Радиус вписанной окружности
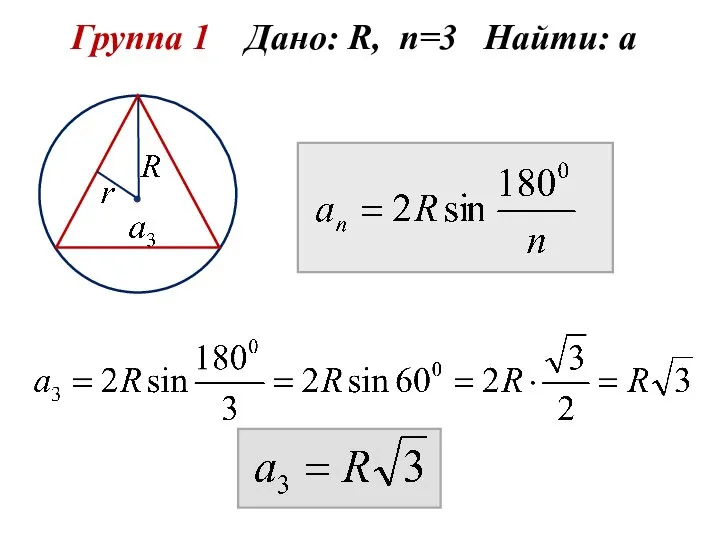
- 7. Группа 1 Дано: R, n=3 Найти: а Группа 2 Дано: R, n=4 Найти: а Группа 3
- 8. Группа 1 Дано: R, n=3 Найти: а
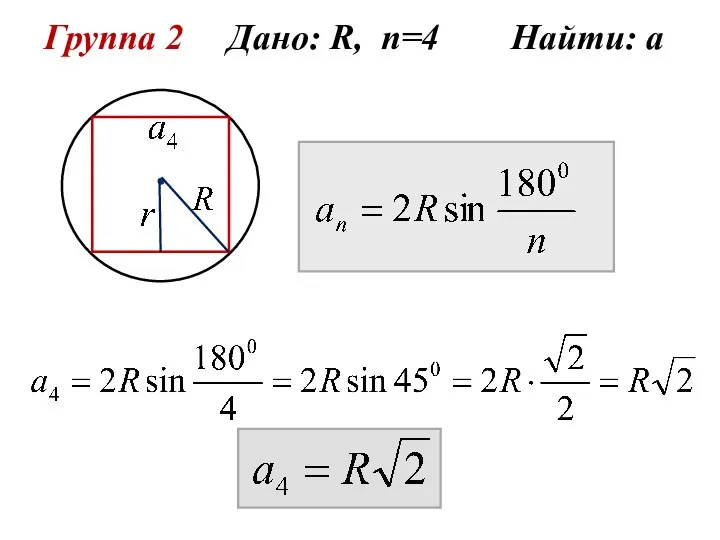
- 9. Группа 2 Дано: R, n=4 Найти: а
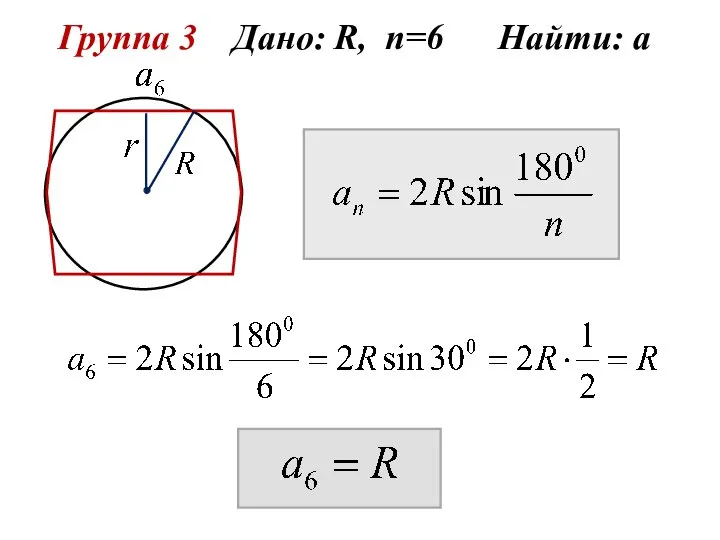
- 10. Группа 3 Дано: R, n=6 Найти: а
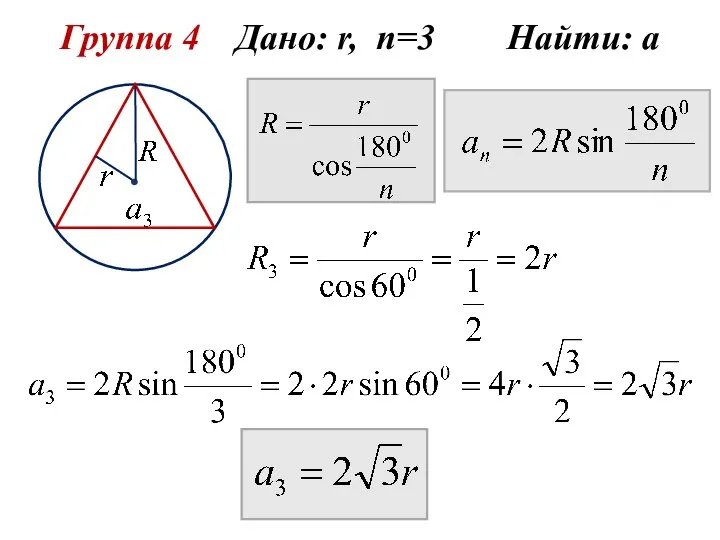
- 11. Группа 4 Дано: r, n=3 Найти: а
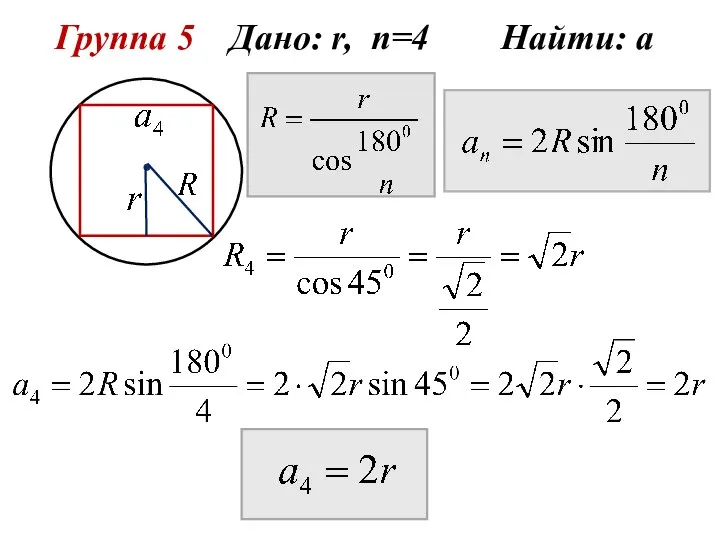
- 12. Группа 5 Дано: r, n=4 Найти: а
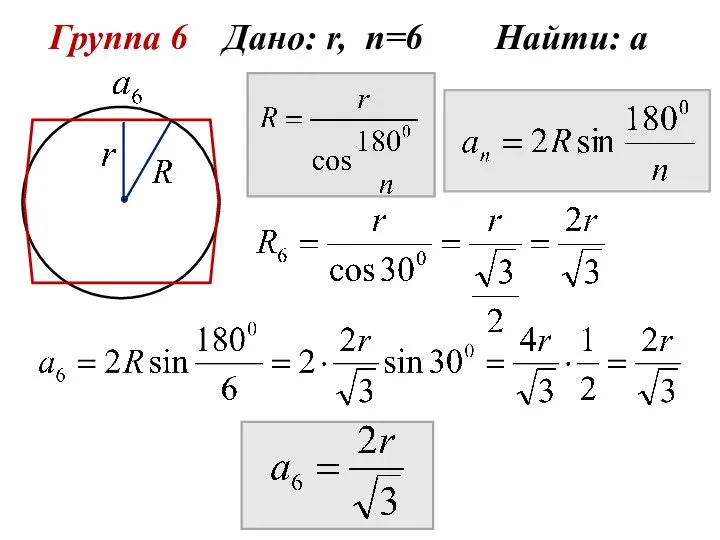
- 13. Группа 6 Дано: r, n=6 Найти: а
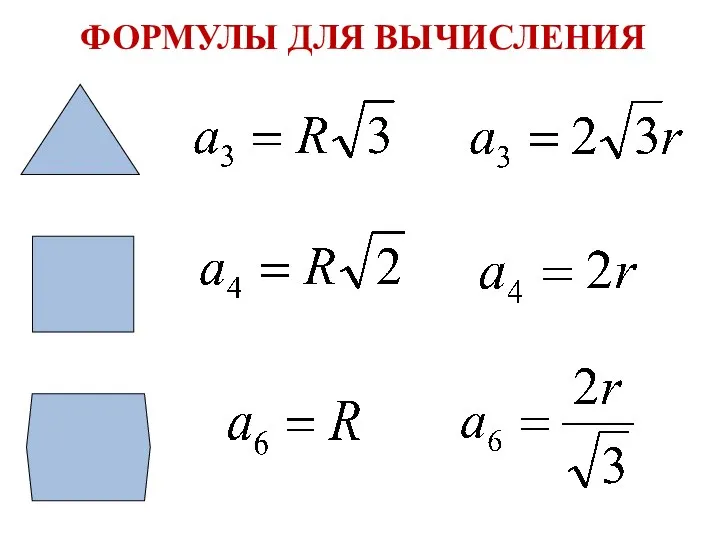
- 14. ФОРМУЛЫ ДЛЯ ВЫЧИСЛЕНИЯ
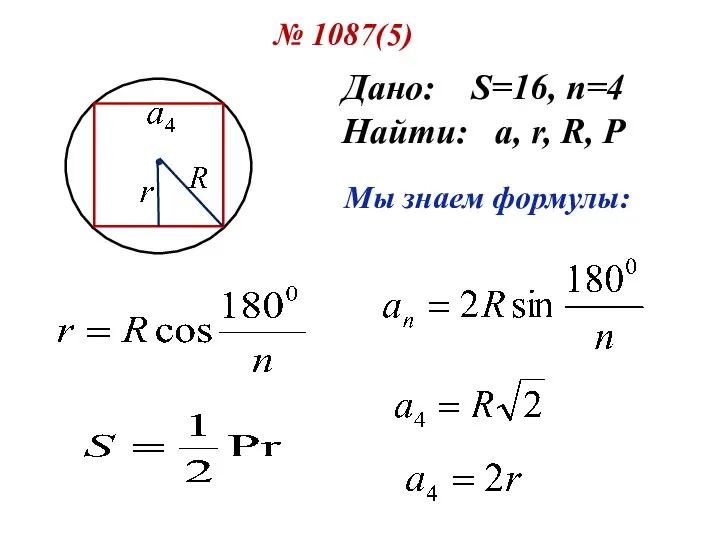
- 15. № 1087(5) Дано: S=16, n=4 Найти: a, r, R, P Мы знаем формулы:
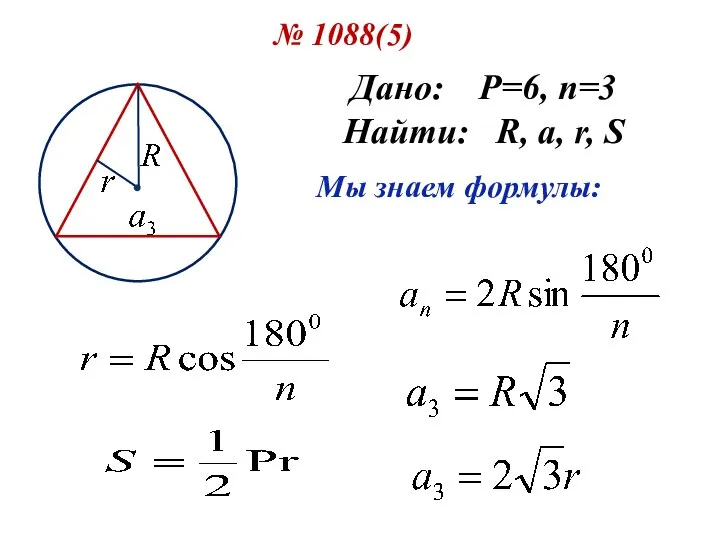
- 16. № 1088(5) Дано: P=6, n=3 Найти: R, a, r, S Мы знаем формулы:
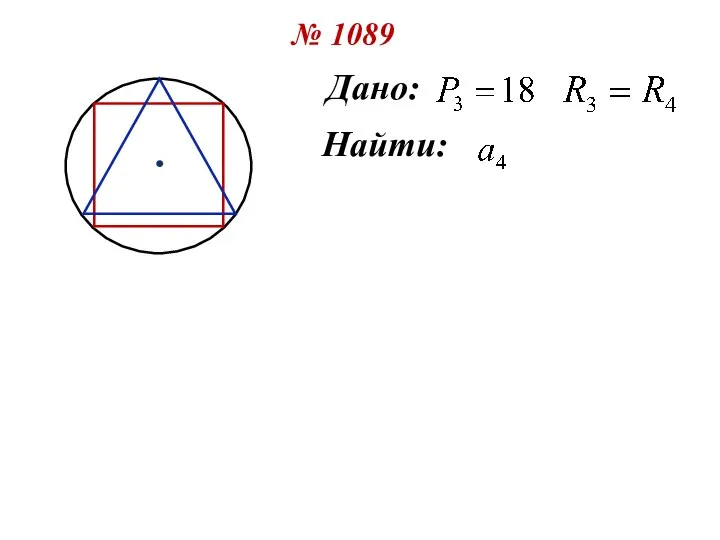
- 17. № 1089 Дано: Найти:
- 18. Подведем итог Мы знаем формулы:
- 20. Скачать презентацию




 Параллельные прямые
Параллельные прямые Исчисление высказываний
Исчисление высказываний Поток событий. Теория вероятностей
Поток событий. Теория вероятностей Статистическая обработка вариационного ряда
Статистическая обработка вариационного ряда Интегралы. Неопределенный интеграл
Интегралы. Неопределенный интеграл Задачи на готовых чертежах. Первый признак равенства треугольников. Устный счёт
Задачи на готовых чертежах. Первый признак равенства треугольников. Устный счёт Вероятность события. Разбор задач
Вероятность события. Разбор задач Монотонность, экстремумы
Монотонность, экстремумы Свойства решений уравнения Левнера
Свойства решений уравнения Левнера Косинусоида. Задание № 9
Косинусоида. Задание № 9 Скалярное произведение векторов
Скалярное произведение векторов Классические алгоритмы решения задачи точного совпадения
Классические алгоритмы решения задачи точного совпадения О сущности понятия функциональная зависимость. Примеры
О сущности понятия функциональная зависимость. Примеры Сложение и вычитание десятичных дробей. 15 февраля в истории Кубани
Сложение и вычитание десятичных дробей. 15 февраля в истории Кубани Построение графика функции
Построение графика функции Щенок Пузырёк. Сложение и вычитание в пределах десяти
Щенок Пузырёк. Сложение и вычитание в пределах десяти Сферические объекты
Сферические объекты Крылатые слова и выражения
Крылатые слова и выражения Презентация на тему Сумма углов треугольника
Презентация на тему Сумма углов треугольника  Задачи. Итоговое повторение
Задачи. Итоговое повторение формулы сокращенного умножения
формулы сокращенного умножения Четные и нечетные числа
Четные и нечетные числа Анализ контрольной работы
Анализ контрольной работы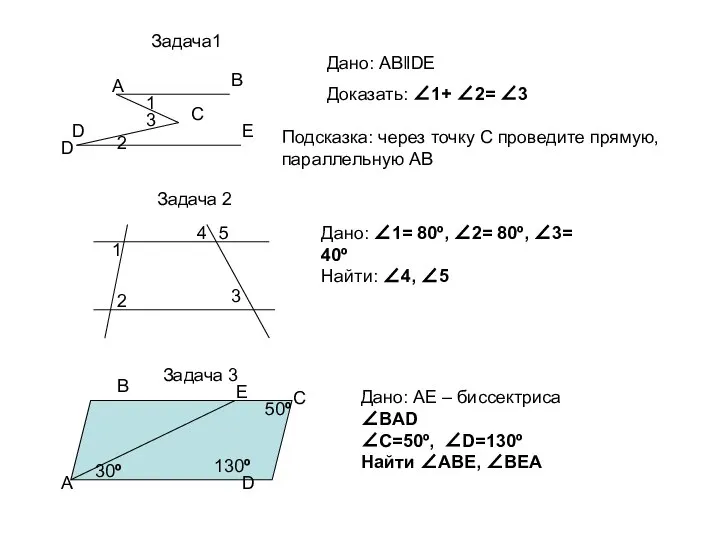 Параллельные прямые (тест)
Параллельные прямые (тест) Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами Теорема Пифагора
Теорема Пифагора Развертка жираф
Развертка жираф Ряды Фурье
Ряды Фурье