Предел функции

Предел функции
Предел – одно из основных понятий математического анализа. Понятие предела использовалось еще Ньютоном во второй половине XVII века и математиками XVIII века, такими как Эйлер и Лагранж, однако они понимали предел интуитивно. Первые строгие определения предела дали Больцано в 1816 году и Коши в 1821 году.
РАЗЛИЧАЮТ – предел функции в точке И предел функции на бесконечности.

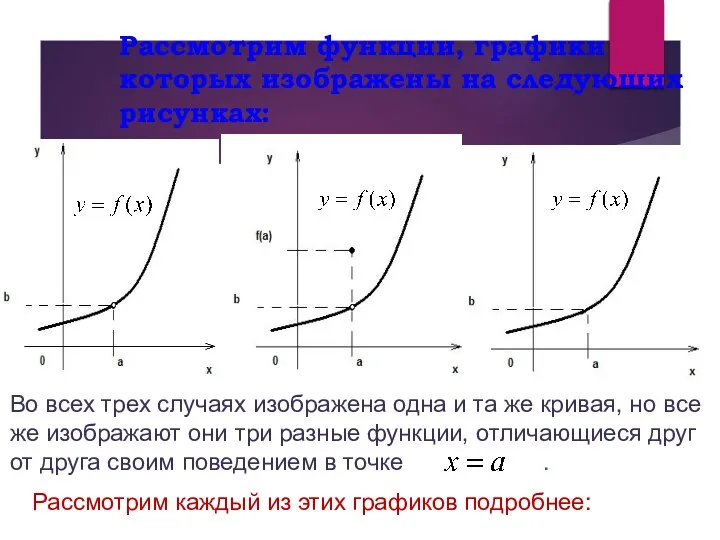
Рассмотрим функции, графики которых изображены на следующих рисунках:
Во всех трех случаях изображена одна и та же кривая, но все же изображают они три разные функции, отличающиеся друг от друга своим поведением в точке
.
Рассмотрим каждый из этих графиков подробнее:

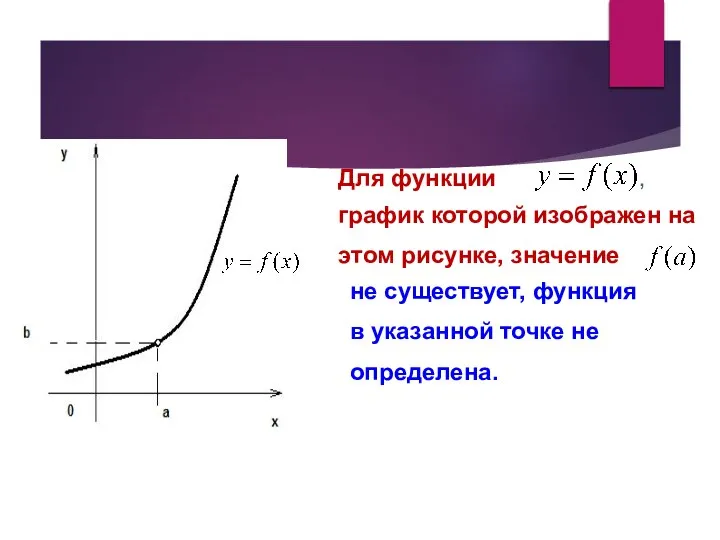
Для функции
график которой изображен на
этом рисунке, значение
,
не существует, функция
в указанной точке не
определена.

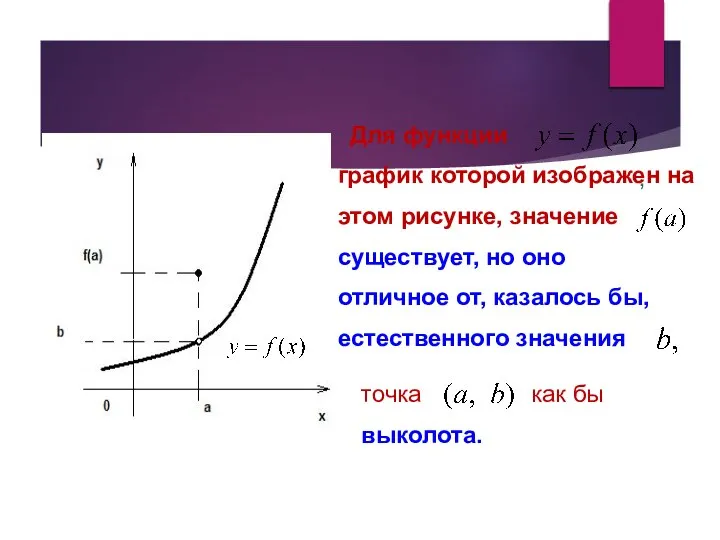
Для функции
график которой изображен на
этом рисунке, значение
,
существует, но оно
отличное от, казалось бы,
естественного значения
точка
как бы
выколота.

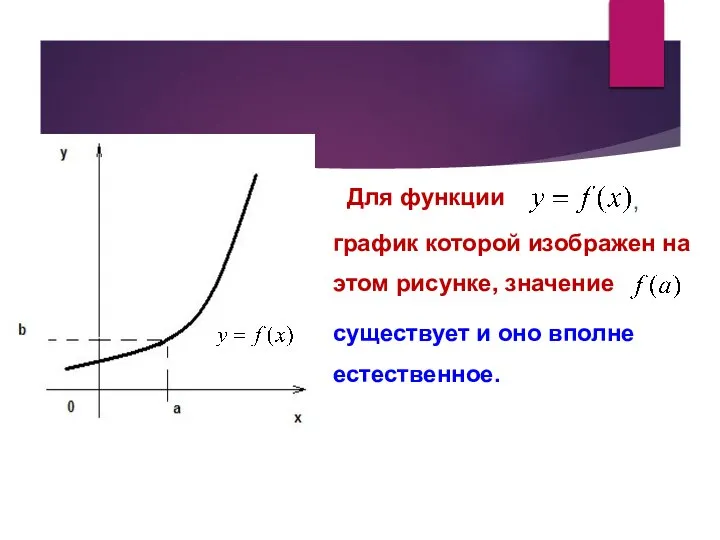
Для функции
график которой изображен на
этом рисунке, значение
,
существует и оно вполне
естественное.

Для всех трех случаев используется одна и та же запись:
которую читают: «предел функции
при
стремлении
к равен ».
Содержательный смысл этой фразы следующий: если значения аргумента выбирать все ближе и ближе к значению
, то значения функции все меньше и меньше
отличаются от предельного значения
Или можно сказать так: в достаточно малой окрестности точки
справедливо приближенное равенство:
При этом сама точка
исключается из рассмотрения.

Прежде чем перейти к разбору решений
примеров заметим, что если предел функции
при стремлении
к
равен значению
функции в точке
, то в таком случае
функцию называют непрерывной.
График такой функции представляет собой
сплошную линию, без «проколов» и «скачков».

Функцию
называют непрерывной
на промежутке
, если она непрерывна в
каждой точке этого промежутка.
Примерами непрерывных функций на всей числовой
прямой являются:
Функция
непрерывна на луче
а
функция
непрерывна на промежутках

Предел функции в точке
Число в называется пределом функции в точке а, если для всех значений х , достаточно близких к а и отличных от а, значение функции f (x) сколь угодно мало отличается
от в.

Теорема.
Если функция f (x) имеет предел в точке х0, то этот предел единственный.

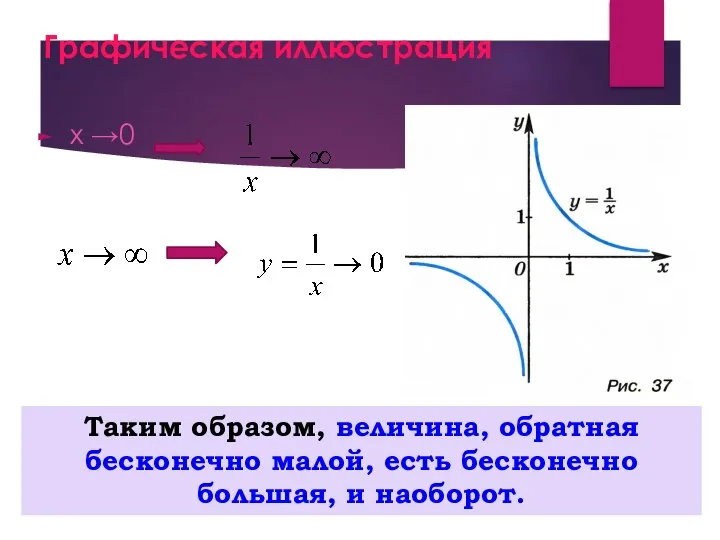
Бесконечно малая функция и бесконечно большая функция.
Функция α (x) называется бесконечно малой при x → a (здесь a – конечное число или ∞), если
Функция f(x) называется бесконечно большой функцией (или бесконечно большой величиной) при х→а, если

Графическая иллюстрация
х →0
Таким образом, величина, обратная бесконечно малой, есть бесконечно большая, и наоборот.

ТЕОРЕМА 1.
Предел СУММЫ (разности) 2-х функций равен СУММЕ (разности) их пределов, если последние существуют:

ТЕОРЕМА 2.
Предел константы равен самой этой константе.

ТЕОРЕМА 3.
Предел ПРОИЗВЕДЕНИЯ 2-х функций равен ПРОИЗВЕДЕНИЮ их пределов, если последние существуют:

ТЕОРЕМА 4.
Предел ОТНОШЕНИЯ 2-х функций равен ОТНОШЕНИЮ их пределов, если последние существуют и ПРЕДЕЛ ЗНАМЕНАТЕЛЯ ОТЛИЧЕН ОТ 0:

ТЕОРЕМА 5.
Постоянный множитель можно выносить за знак предела

ТЕОРЕМА 6.
Предел степени переменного равен той же степени предела основания:

Вычисление пределов
Вычисление предела:
начинают с подстановки предельного значения x0 в функцию f(x).
Если при этом получается конечное число, то предел равен этому числу.
Если при подстановки предельного значения x0 в функцию f(x) получаются выражения вида:
то предел будет равен:

Вычислить пределы:

Примеры

Вычисление пределов
Часто при подстановке предельного значения x0 в функцию f(x) получаются выражения следующих видов:
Эти выражения называются неопределенности, а вычисление пределов в этом случае называется раскрытие неопределенности.

Упражнения: