Содержание
- 2. Леона́рдо Пиза́нский — первый крупный математик средневековой Европы. Наиболее известен под прозвищем Фибона́ччи. Леонардо Пизанский никогда
- 3. Около 1200 года н.э человек по имени Леонардо Пизанский, более известный как, Фибоначчи открыл последовательность чисел
- 4. Каждое следующее число получается путём суммирования двух предыдущих: 0+1=1 1+1=2 1+2=3 2+3=5 3+5=8 5+8=13
- 5. Кстати, есть ещё одна интересная вещь. Если мы возьмём два соседних числа из последовательности Фибоначчи и
- 6. Прямоугольник с шириной и высотой равными двумя соседним числам последовательности (8 и 13) представляет собой так
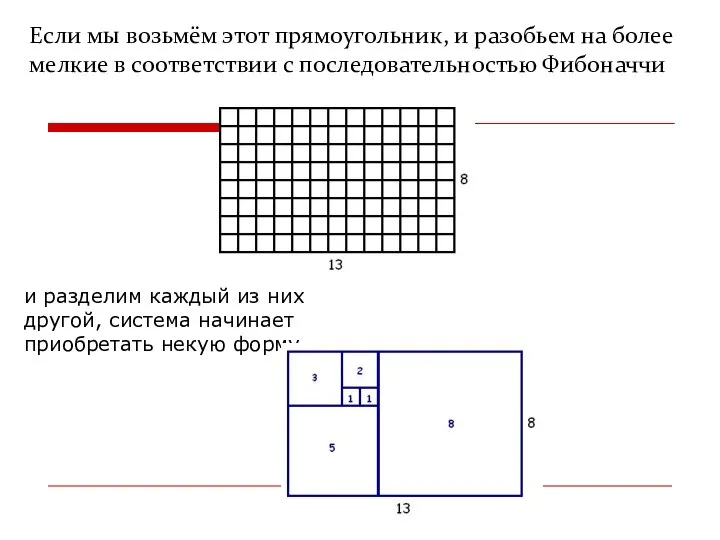
- 7. Если мы возьмём этот прямоугольник, и разобьем на более мелкие в соответствии с последовательностью Фибоначчи и
- 8. мы увидим так называемую «спираль Фибоначчи». Сама спираль не представляет ничего особенного важно то, где мы
- 9. Возьмём, к примеру, подсолнух расположение его семечек представляет собой идеальную последовательность спиралей по 55, 44 и
- 10. Ячейки ананаса создают точно такую же спиральную последовательность, как в прочем и сама шишка.
- 11. Когда потоки воды двигаются по океану и волны прилива подходят к берегу они изгибаются в форме
- 12. Ветви деревьев, ракушки, морские звёзды, цветы и особенно раковины моллюсков сформированы по той же самой схеме(золотой
- 13. Эта схема может также быть замечена вокруг нас и в нашей каждодневной жизни, но самый потрясающий
- 14. На расстоянии приблизительно в 100000 световых лет даже спирали галактик сформированы по абсолютно такому же признаку,
- 18. Скачать презентацию














 Измерение размеров деталей с помощью штангенциркуля
Измерение размеров деталей с помощью штангенциркуля Методы общения линейных уравнений с тремя неизвестными
Методы общения линейных уравнений с тремя неизвестными Лекция. Матрицы.Операции над матрицами.Определители матриц 2 и 3 порядка
Лекция. Матрицы.Операции над матрицами.Определители матриц 2 и 3 порядка Квадратный корень. Математический диктант
Квадратный корень. Математический диктант Изучение нумерации числе учащимися пятых классов с легкой степенью умстенной отсталости
Изучение нумерации числе учащимися пятых классов с легкой степенью умстенной отсталости Числовые ряды
Числовые ряды Формулы сокращенного умножения. Подготовка к СОР
Формулы сокращенного умножения. Подготовка к СОР Задачи на построение
Задачи на построение Математическая логика
Математическая логика Презентация на тему АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ ПРОИЗВОЛЬНЫХ СТЕПЕНЕЙ
Презентация на тему АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ ПРОИЗВОЛЬНЫХ СТЕПЕНЕЙ  Линейные дифференциальные уравнения первого порядка
Линейные дифференциальные уравнения первого порядка Презентация на тему Радианная мера углов и дуг
Презентация на тему Радианная мера углов и дуг  Методическая разработка по математике. Тема: Треугольники
Методическая разработка по математике. Тема: Треугольники Вычитание чисел. Решение уравнений
Вычитание чисел. Решение уравнений Элементы комбинаторики
Элементы комбинаторики Контрольная работа
Контрольная работа Параллелограмм
Параллелограмм Кафедра математики МБОУ лицея № 14 г. Ставрополя
Кафедра математики МБОУ лицея № 14 г. Ставрополя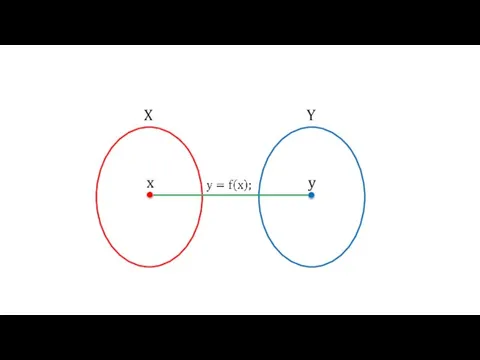 Определение и способы задания числовой функции
Определение и способы задания числовой функции Математические кривые в природе и технике
Математические кривые в природе и технике Показательные уравнения и неравенства
Показательные уравнения и неравенства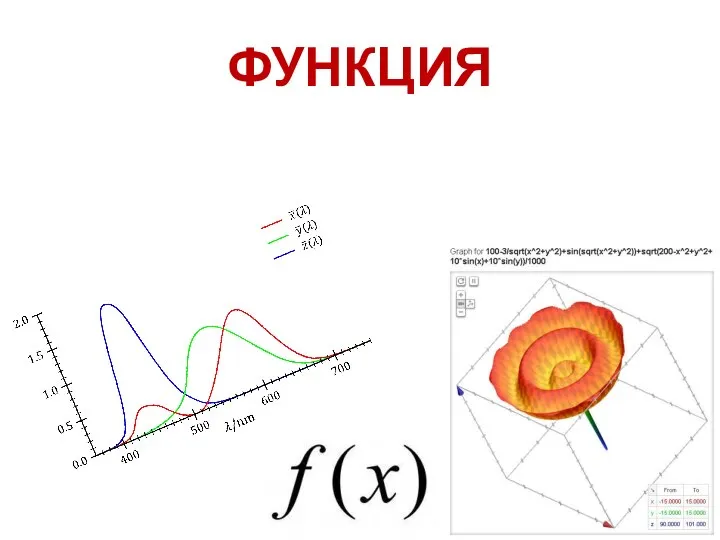 Понятие функции
Понятие функции Пропорция. Основное свойство пропорции
Пропорция. Основное свойство пропорции Интерпретация графиков реальной зависимости
Интерпретация графиков реальной зависимости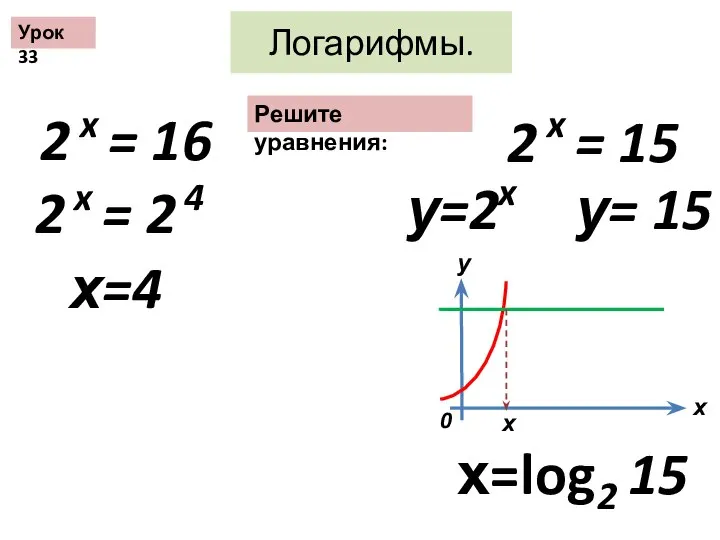 Логарифмы
Логарифмы Решение задач
Решение задач Сложение и вычитание дробей
Сложение и вычитание дробей Интегральные уравнения
Интегральные уравнения