Исследование функции с помощью производной

Цели урока:
1. Обобщить знания учащихся по теме «Исследование функции на монотонность и экстремумы» и выяснить степень готовности учащихся к контрольной работе.
2. Способствовать развитию навыков применения теоретических знаний в практической деятельности.
3. Способствовать воспитанию ответственности за качество и результат выполняемой работы на уроке

Задачи:
Повторить алгоритм исследования функции на монотонность и экстремумы с помощью производной.
Используя алгоритмы исследования функций с помощью производной, применить их для решения конкретных задач.
Формировать глубину и оперативность мышления.

Устный опрос
Что значит исследовать функцию на монотонность?
Можно ли по знаку производной определить характер монотонности функции на промежутке? Ответ поясните.
Для какой функции на промежутке выполняется равенство f'(x)=0?
Какие точки области определения функции называются стационарными, критическими?
Какие точки называются точками экстремума функции?
В каком случае стационарная или критическая точка является точкой экстремума, а в каком – не является? Приведите условную схему для знаков производной.
Каков алгоритм исследования непрерывной функции на монотонность и экстремумы?

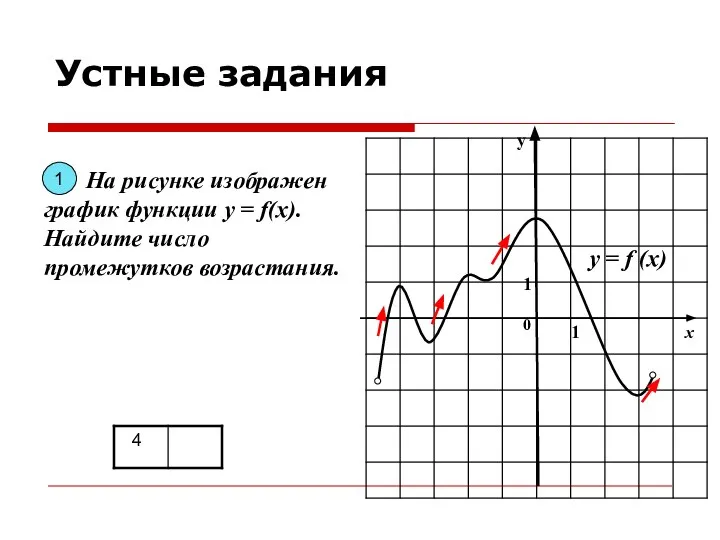
у
х
0
1
1
На рисунке изображен график функции у = f(x). Найдите число промежутков возрастания.
y = f (x)
Устные задания
1

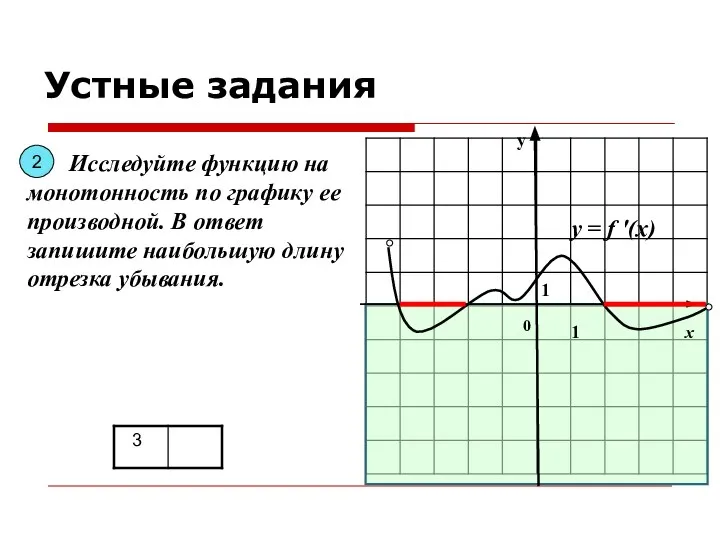
у
х
0
1
1
Исследуйте функцию на монотонность по графику ее производной. В ответ запишите наибольшую длину отрезка убывания.
y = f ′(x)
Устные задания
2

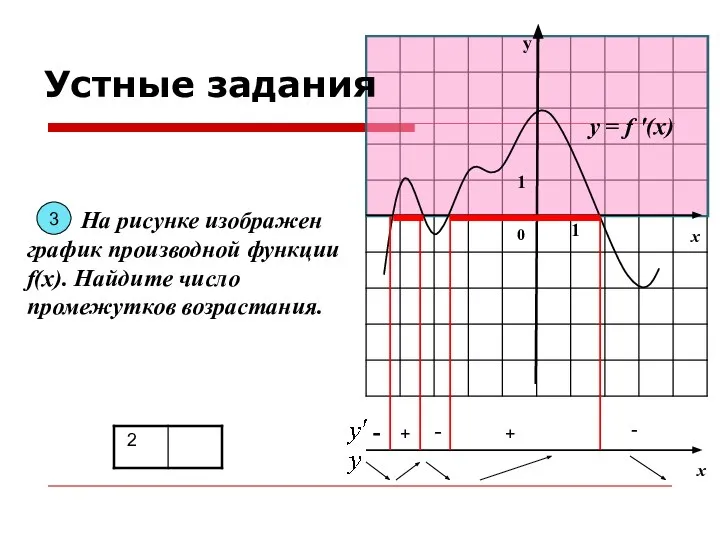
у
х
0
1
1
На рисунке изображен график производной функции f(x). Найдите число промежутков возрастания.
y = f ′(x)
+
+
-
-
-
х
Устные задания
3

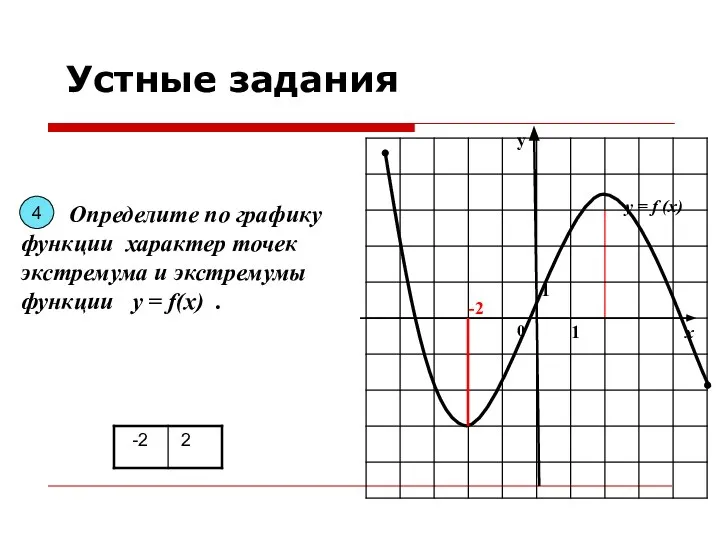
у
х
0
1
1
Определите по графику функции характер точек экстремума и экстремумы функции y = f(x) .
y = f (x)
-2
Устные задания
4

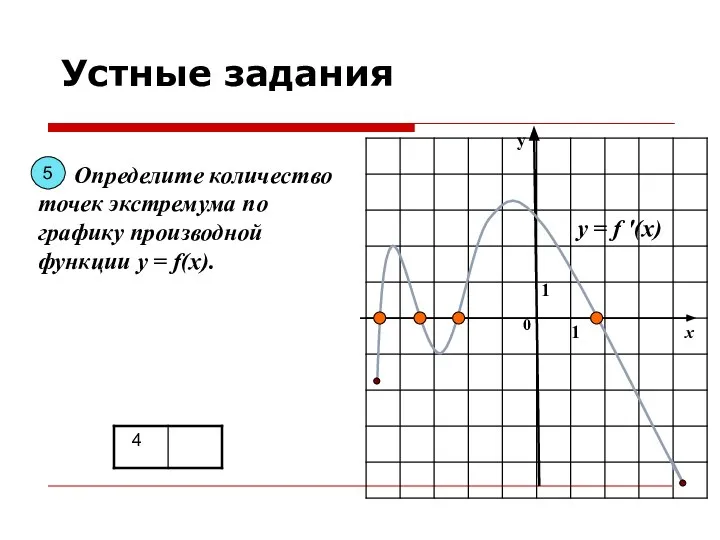
у
х
0
1
1
Определите количество точек экстремума по графику производной функции y = f(x).
y = f ′(x)
Устные задания
5

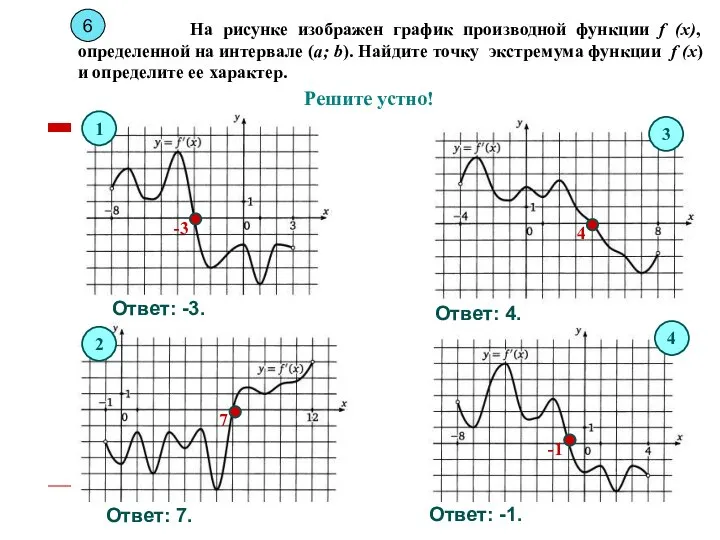
На рисунке изображен график производной функции f (x), определенной на интервале (a; b). Найдите точку экстремума функции f (x) и определите ее характер.
Решите устно!
1
3
4
2
6

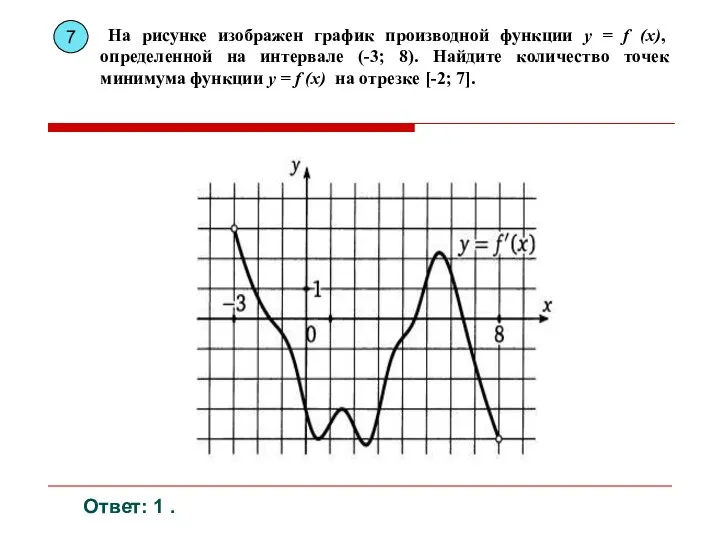
Ответ: 1 .
На рисунке изображен график производной функции y = f (x), определенной на интервале (-3; 8). Найдите количество точек минимума функции y = f (x) на отрезке [-2; 7].
7

Задания ЕГЭ (В8)
1. На рисунке изображен график производной функции f (x), определенной на интервале (a; b). Найдите точку экстремума функции f (x) .
2. На рисунке изображен график производной функции y = f (x), определенной на интервале (x1; x2). Найдите количество точек максимума (минимума) функции y = f (x) на отрезке [a; b].
3. На рисунке изображен график производной функции f(x), определенной на интервале (x1; x2). Найдите промежутки возрастания (убывания) функции f(x).

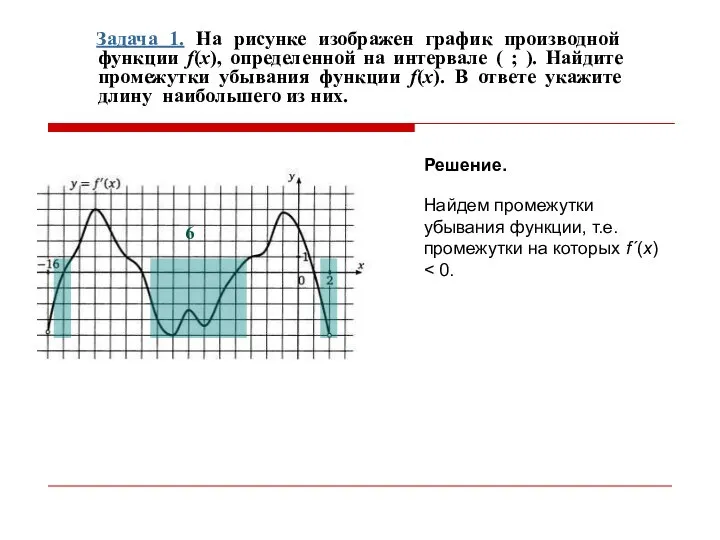
Задача 1. На рисунке изображен график производной функции f(x), определенной на интервале ( ; ). Найдите промежутки убывания функции f(x). В ответе укажите длину наибольшего из них.
Найдем промежутки убывания функции, т.е. промежутки на которых f´(x) < 0.
Решение.
6

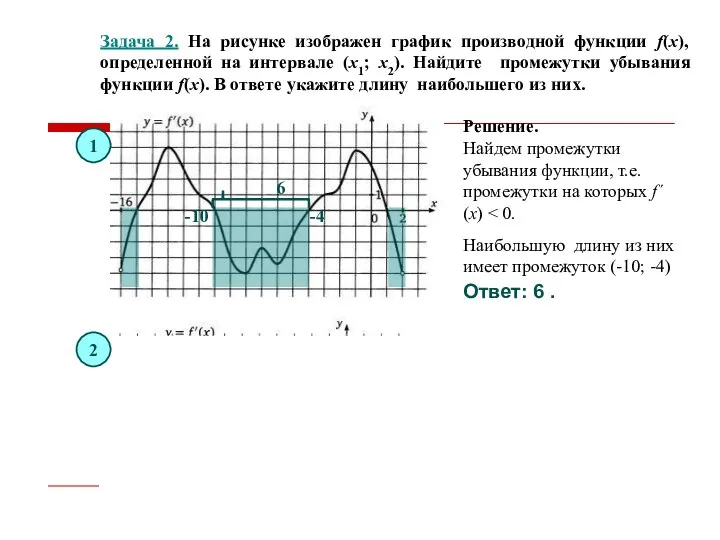
Задача 2. На рисунке изображен график производной функции f(x), определенной на интервале (x1; x2). Найдите промежутки убывания функции f(x). В ответе укажите длину наибольшего из них.
1
Решение.
Решение.
Ответ: 6 .
Ответ: 3 .
Найдем промежутки убывания функции, т.е. промежутки на которых f´(x) < 0.
Наибольшую длину из них имеет промежуток (-10; -4)
-10
-4
Решение аналогично: ищем промежутки на которых f´(x) < 0.
Наибольший из них имеет длину равную 3.
6
3
2

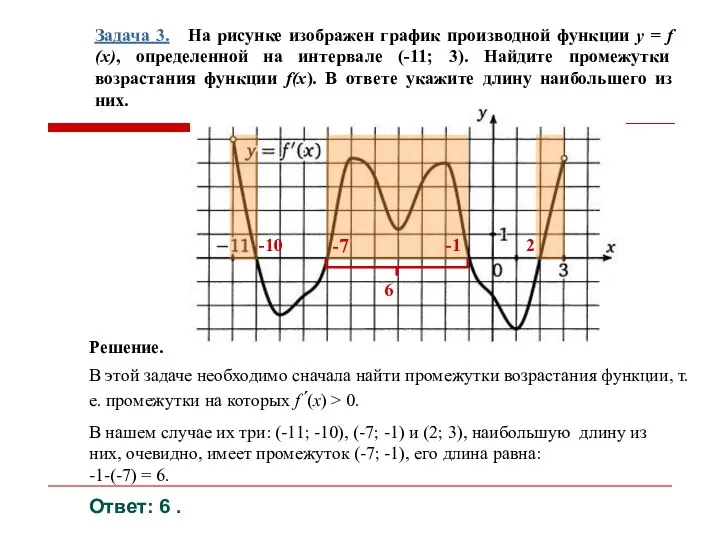
Задача 3. На рисунке изображен график производной функции y = f (x), определенной на интервале (-11; 3). Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.
В этой задаче необходимо сначала найти промежутки возрастания функции, т.е. промежутки на которых f´(x) > 0.
Решение.
В нашем случае их три: (-11; -10), (-7; -1) и (2; 3), наибольшую длину из них, очевидно, имеет промежуток (-7; -1), его длина равна:
-1-(-7) = 6.
Ответ: 6 .
-10
-7
-1
2
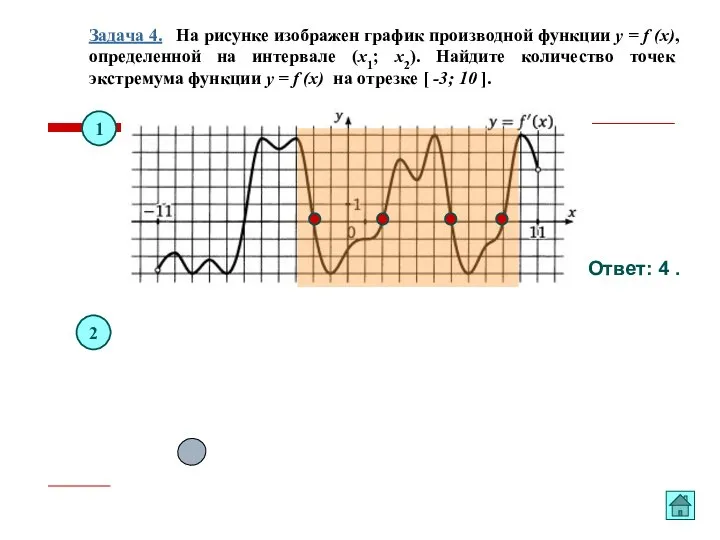
6

Задача 4. На рисунке изображен график производной функции y = f (x), определенной на интервале (x1; x2). Найдите количество точек экстремума функции y = f (x) на отрезке [ -3; 10 ].
Ответ: 4 .
Ответ: 4 .
1
2

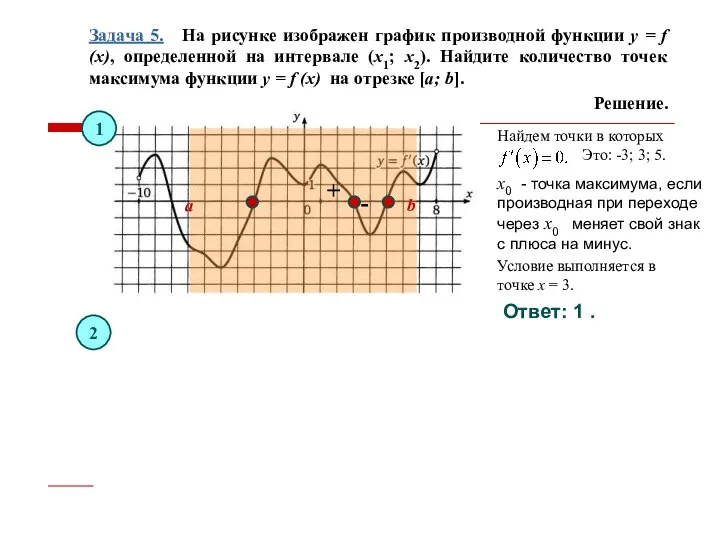
Задача 5. На рисунке изображен график производной функции y = f (x), определенной на интервале (x1; x2). Найдите количество точек максимума функции y = f (x) на отрезке [a; b].
Решение.
Ответ: 1 .
Ответ: 3 .
a
b
a
b
x0 - точка максимума, если производная при переходе через x0 меняет свой знак с плюса на минус.
-
+
Условие выполняется в точке x = 3.
Решение.
Условие выполняется в точках: -1; 8; 13.
1
Решение аналогично.
2