Содержание
- 2. Предельный доход (предельная выручка). Пусть Q – объем произведенной продукции. R(Q) – доход от ее реализации.
- 3. то Если если мало. Предельный доход показывает дополнитель- ный доход от реализации дополнительной единицы продукции. Предельный
- 4. Эластичность в экономике. Эластичность показывает на сколько процентов изменится функция при изменении аргумента на 1%.
- 5. Эластичность в экономике. Пусть Q(P) – функция спроса от цены. - показывает на сколько процентов изменится
- 6. Эластичность в экономике. Если то спрос называют эластичным. Если то спрос называют неэластичным. Если то спрос
- 7. Соотношение эластичности спроса и предельного дохода. Пусть Q(P) – функция спроса на некоторый товар; R(P)=P·Q(P) –
- 8. Соотношение эластичности спроса и предельного дохода. Если т.е. спрос эластичен, то т.е. увеличение цены приведет к
- 9. Соотношение эластичности спроса и предельного дохода. Если т.е. спрос неэластичен, то т.е. увеличение цены приведет к
- 10. Соотношение эластичности спроса и предельного дохода. Если т.е. спрос с единичной т.е. увеличение цены не изменит
- 11. Соотношение эластичности спроса и предельного дохода. Вывод: С возрастанием цены для продукции с эластичным спросом суммарный
- 12. Работа № 1 Функция спроса на некоторый товар Q(P)=-aP+b при P b/a, где a – последняя
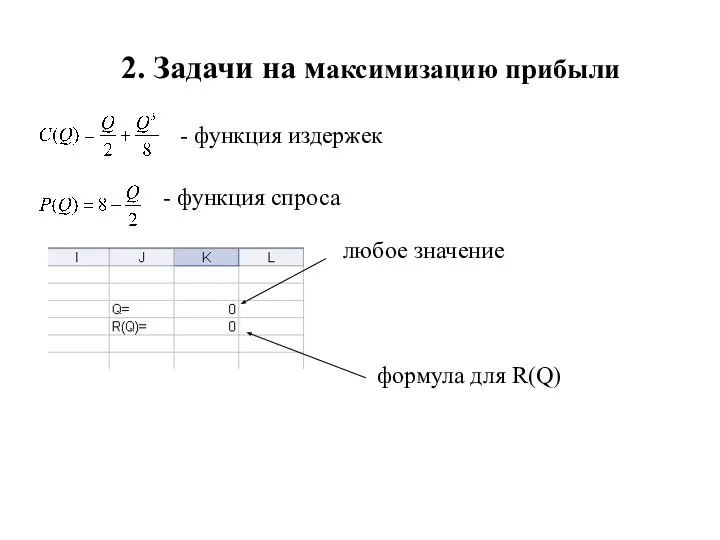
- 13. 2. Задачи на максимизацию прибыли - функция издержек - функция спроса Составить функцию прибыли П(Q) Найти
- 14. 2. Задачи на максимизацию прибыли - функция издержек - функция спроса любое значение формула для R(Q)
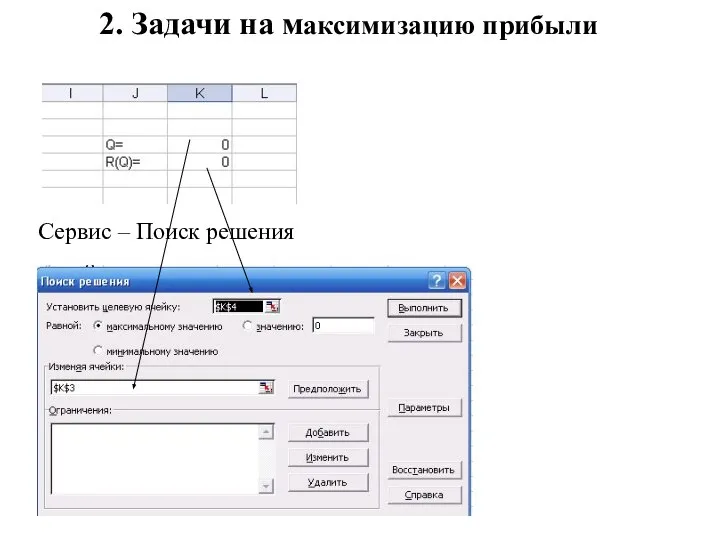
- 15. 2. Задачи на максимизацию прибыли Сервис – Поиск решения
- 16. 2. Задачи на максимизацию прибыли
- 17. 2. Задачи на максимизацию прибыли - функция издержек - функция спроса Составить функцию прибыли П(Q) Найти
- 18. Работа 2. Задачи на максимизацию прибыли Вариант 1 4.181; Вариант 2 4.182; Вариант 3 4.184 Вариант
- 19. 3. Задачи на максимизацию прибыли функций двух и более переменных Пример 1 Фирма производит 2 товара
- 20. Необходимое условие экстремума. Пусть - точка экстремума функции z=f(x,y). Тогда
- 21. Если то - точка максимума Если то - точка минимума Если то не является точкой экстремума
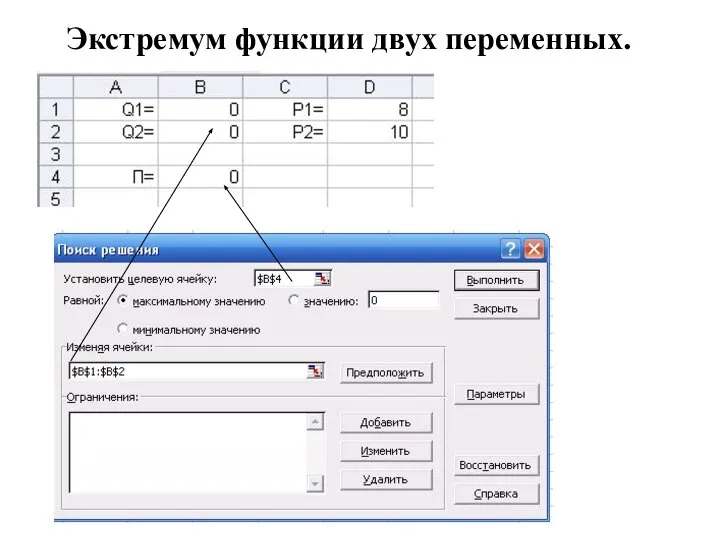
- 22. Экстремум функции двух переменных. Пример 1 Фирма производит 2 товара и продает их по ценам 8
- 23. Экстремум функции двух переменных.
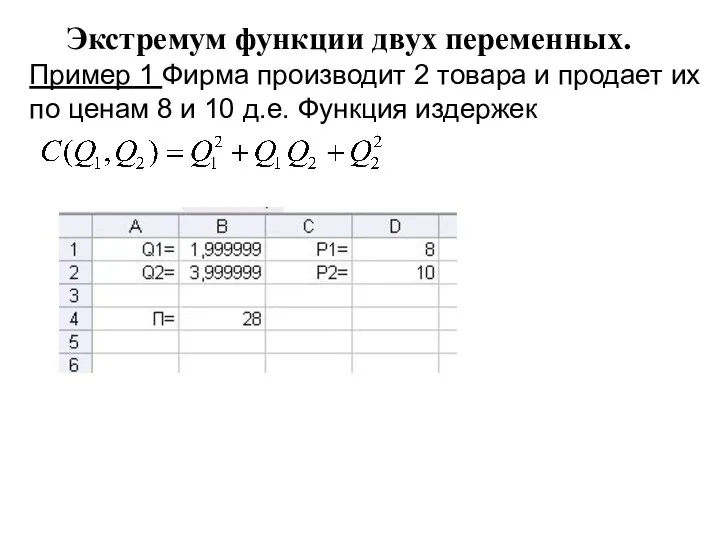
- 24. Экстремум функции двух переменных. Пример 1 Фирма производит 2 товара и продает их по ценам 8
- 25. Работа 3. Задачи на максимизацию прибыли функций двух и более переменных Вариант 1 5.229 Вариант 2
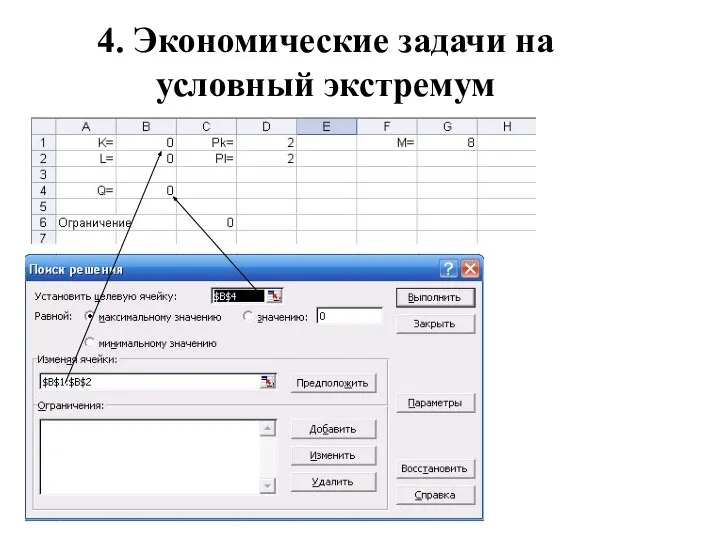
- 26. 4. Экономические задачи на условный экстремум Пример. Q(K,L)=KL – производственная функция. Единица капитала стоит 2 д.е.,
- 27. 4. Экономические задачи на условный экстремум Пример. Q(K,L)=KL – производственная функция. Единица капитала стоит 2 д.е.,
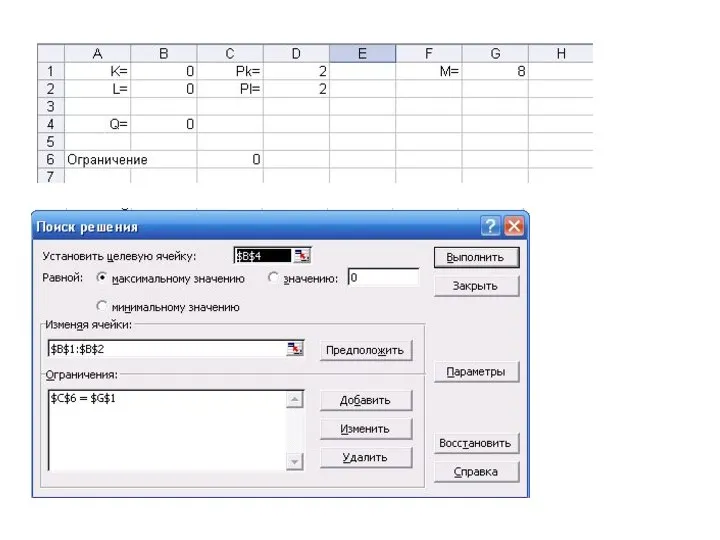
- 28. 4. Экономические задачи на условный экстремум
- 29. 4. Экономические задачи на условный экстремум
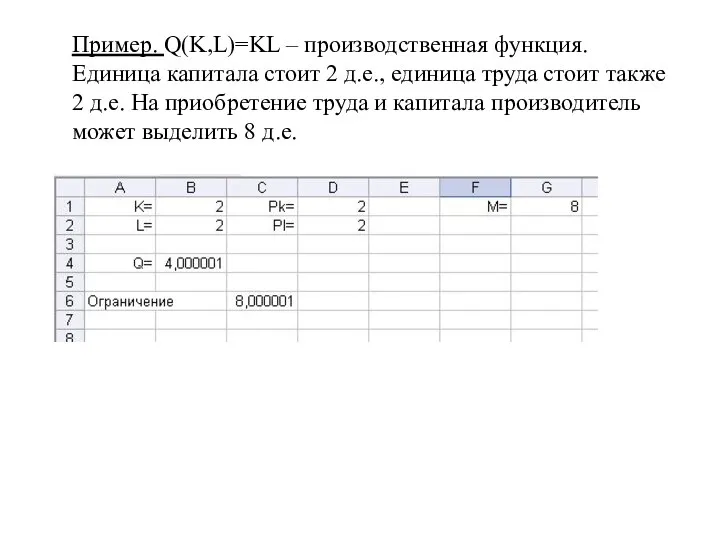
- 31. Пример. Q(K,L)=KL – производственная функция. Единица капитала стоит 2 д.е., единица труда стоит также 2 д.е.
- 33. Скачать презентацию























 Вычисление одномерных, двумерных и интегралов c переменным верхним пределом
Вычисление одномерных, двумерных и интегралов c переменным верхним пределом The determinant of a matrix. Part 3-1
The determinant of a matrix. Part 3-1 Линейные неравенства с одной переменной. Обобщающий урок
Линейные неравенства с одной переменной. Обобщающий урок Решение систем уравнений
Решение систем уравнений Музыкалық аспаптарға
Музыкалық аспаптарға Решение задач на вычисление площадей четырехугольников
Решение задач на вычисление площадей четырехугольников Презентация на тему Делимое и делитель (2 класс)
Презентация на тему Делимое и делитель (2 класс)  Построение сечений многогранников. Задачи
Построение сечений многогранников. Задачи Деление двузначных чисел
Деление двузначных чисел Многоугольники в жизни
Многоугольники в жизни Ось симметрии фигуры
Ось симметрии фигуры Многоугольники в окружающем нас мире
Многоугольники в окружающем нас мире Арифметические пятиминутки
Арифметические пятиминутки Нефть. Добыча, переработка, использование. Задачи на нахождение объёма цилиндра. Работа с формулами в таблице Excel
Нефть. Добыча, переработка, использование. Задачи на нахождение объёма цилиндра. Работа с формулами в таблице Excel Презентация на тему РЕШЕНИЕ СИСТЕМ УРАВНЕНИЙ ВТОРОЙ СТЕПЕНИ
Презентация на тему РЕШЕНИЕ СИСТЕМ УРАВНЕНИЙ ВТОРОЙ СТЕПЕНИ  Основное свойство дроби
Основное свойство дроби Готовимся к Всероссийским проверочным работам по математике
Готовимся к Всероссийским проверочным работам по математике Великая Отечественная война в числах
Великая Отечественная война в числах Я сдам ЕГЭ. Кинематика
Я сдам ЕГЭ. Кинематика Решение логических задач табличным способом
Решение логических задач табличным способом Презентация 1
Презентация 1 Решение уравнения в 1 классе
Решение уравнения в 1 классе Дискретная математика. Повторение арифметических действий
Дискретная математика. Повторение арифметических действий Сумма n первых членов геометрической прогрессии (9 класс)
Сумма n первых членов геометрической прогрессии (9 класс) Преобразование графиков функций
Преобразование графиков функций Сравнение десятичных дробей
Сравнение десятичных дробей Задачи на подсчет числа размещений, перестановок, сочетаний
Задачи на подсчет числа размещений, перестановок, сочетаний Открытый урок «Математический бой» 11класс
Открытый урок «Математический бой» 11класс