Слайд 2После построения модели регрессии необходимо проверить выполнение предпосылок МНК, т.к. нарушение этих

условий снижает качество модели.
Слайд 3Предпосылки МНК
Коэффициенты регрессии, найденные исходя из системы нормальных уравнений, представляют собой

выборочные оценки характеристики силы связи.
Для практических целей важно, чтобы они были несмещенными, эффективными и состоятельными.
Слайд 4 МНК строит оценки регрессии на основе минимизации суммы квадратов остатков. Поэтому

очень важно исследовать поведение остаточных величин регрессии εi.
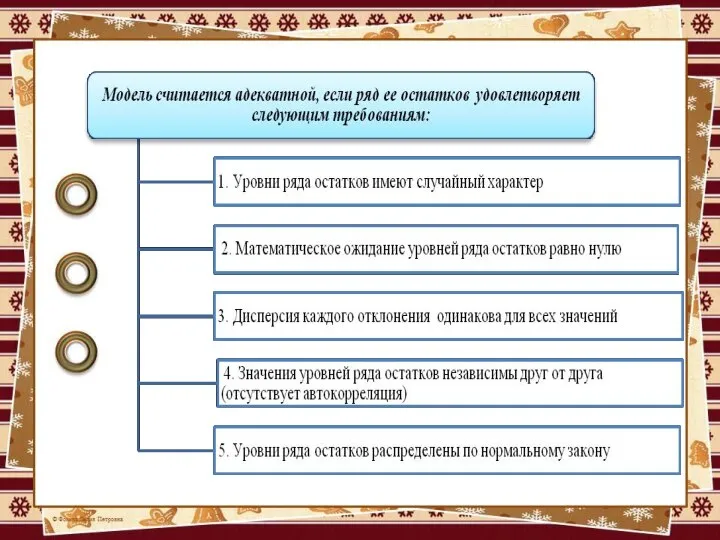
Исследование остатков предполагает проверку наличия пяти предпосылок, которые называются условиями Гаусса-Маркова.
Слайд 5Теорема Гаусса-Маркова:
Оценки параметров линейной регрессии, полученные МНК, будут несмещенными и эффективными в

классе линейных несмещенных оценок при выполнении ряда условий
(условий Гаусса-Маркова или предпосылок МНК).









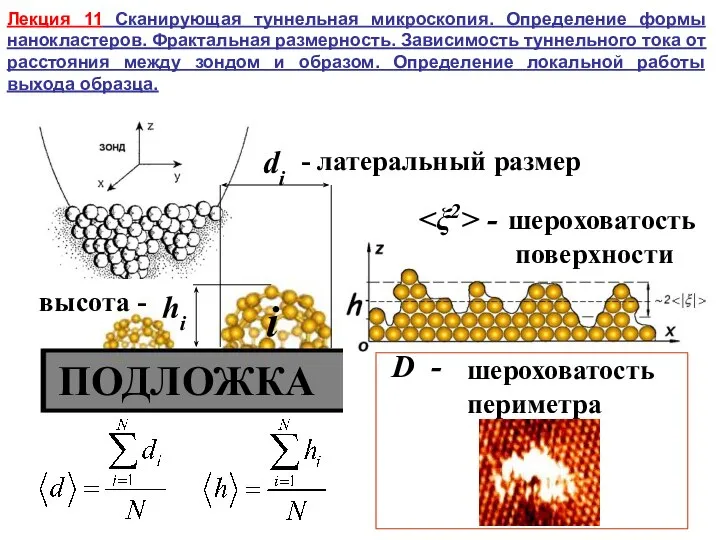 Сканирующая туннельная микроскопия. Определение формы нанокластеров. Фрактальная размерность
Сканирующая туннельная микроскопия. Определение формы нанокластеров. Фрактальная размерность Аксиомы стереометрии
Аксиомы стереометрии Матрицы
Матрицы Смежные и вертикальные углы. Решение задач
Смежные и вертикальные углы. Решение задач Подготовка к диагностической работе. 5 класс
Подготовка к диагностической работе. 5 класс Презентация на тему Решение задач В10 (ЕГЭ 2012)
Презентация на тему Решение задач В10 (ЕГЭ 2012)  Интересные факты про математику
Интересные факты про математику Презентация на тему СОСТАВ ЧИСЕЛ ПЕРВОГО ДЕСЯТКА
Презентация на тему СОСТАВ ЧИСЕЛ ПЕРВОГО ДЕСЯТКА  Двойные и тройные интегралы
Двойные и тройные интегралы Тригонометрические уравнения. Методы решения тригонометрических уравнений
Тригонометрические уравнения. Методы решения тригонометрических уравнений Функция y=k/x, её график и свойства
Функция y=k/x, её график и свойства Параллельность в пространстве
Параллельность в пространстве Понятие объёма
Понятие объёма Фукция синус и косинус
Фукция синус и косинус Нахождение числа по его процентам
Нахождение числа по его процентам Matching Game
Matching Game Окружность. Методическая разработка урока
Окружность. Методическая разработка урока Наглядная геометрия
Наглядная геометрия Оцінки типу Височанського-Петуніна в класі чистих неперервних типів розподілів
Оцінки типу Височанського-Петуніна в класі чистих неперервних типів розподілів Тема 6_2022
Тема 6_2022 Математика и спорт
Математика и спорт Викторина по математике: Где логика?
Викторина по математике: Где логика? Обратные тригонометрические функции
Обратные тригонометрические функции Презентация на тему Небесная геометрия - снежинки
Презентация на тему Небесная геометрия - снежинки  Арифметическая прогрессия в медицине и биологии
Арифметическая прогрессия в медицине и биологии Решение показательных неравенств
Решение показательных неравенств Сравнение, сложение и вычитание дробей с разными знаменателями
Сравнение, сложение и вычитание дробей с разными знаменателями Планиметрия: задачи, связанные с углами. Применение тригонометрии в геометрических задачах
Планиметрия: задачи, связанные с углами. Применение тригонометрии в геометрических задачах