Содержание
- 2. Цели: 1) Систематизировать приемы построения графиков. 2) Показать их применение при построении: а) графиков сложных функций;
- 3. Рассмотрим основные правила преобразования графиков на примерах элементарных функций
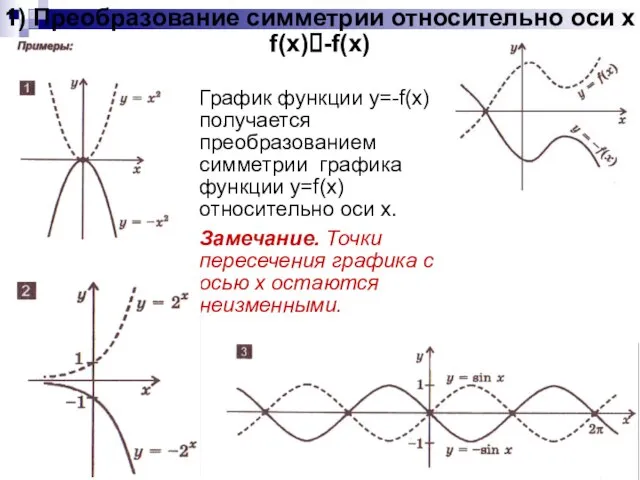
- 4. 1) Преобразование симметрии относительно оси x f(x)?-f(x) График функции y=-f(x) получается преобразованием симметрии графика функции y=f(x)
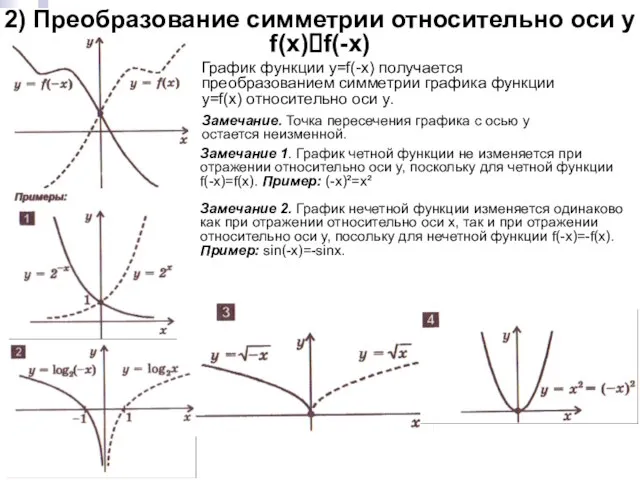
- 5. 2) Преобразование симметрии относительно оси y f(x)?f(-x) График функции y=f(-x) получается преобразованием симметрии графика функции y=f(x)
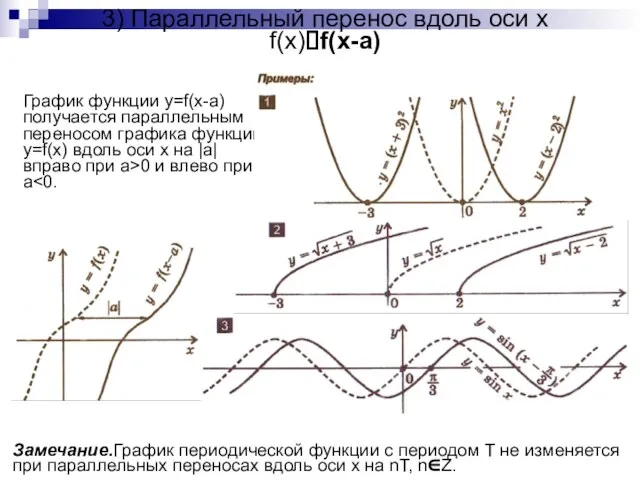
- 6. 3) Параллельный перенос вдоль оси x f(x)?f(x-a) График функции y=f(x-a) получается параллельным переносом графика функции y=f(x)
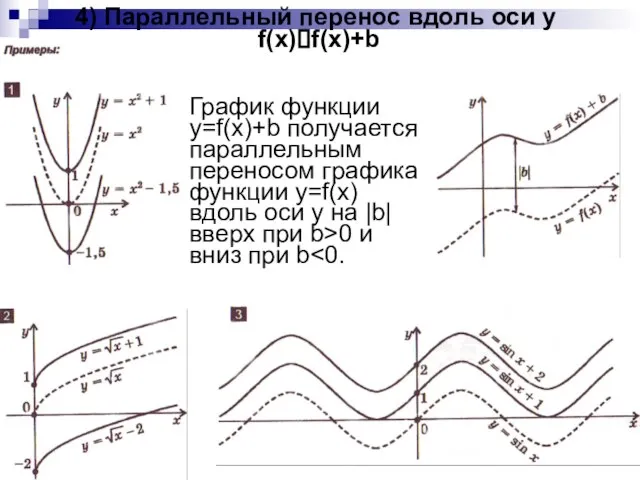
- 7. 4) Параллельный перенос вдоль оси y f(x)?f(x)+b График функции y=f(x)+b получается параллельным переносом графика функции y=f(x)
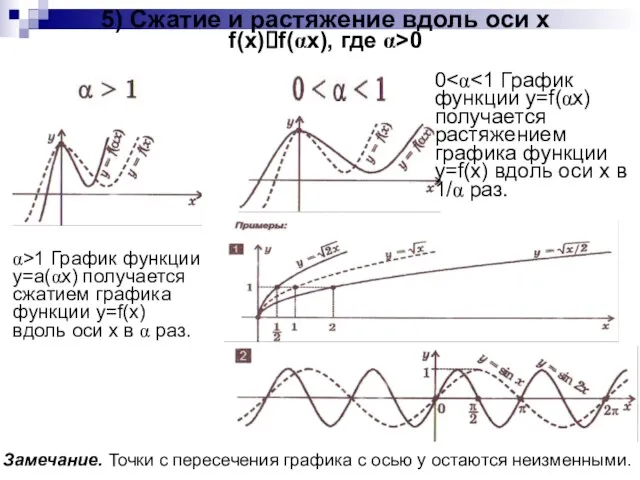
- 8. 5) Сжатие и растяжение вдоль оси x f(x)?f(αx), где α>0 α>1 График функции y=а(αx) получается сжатием
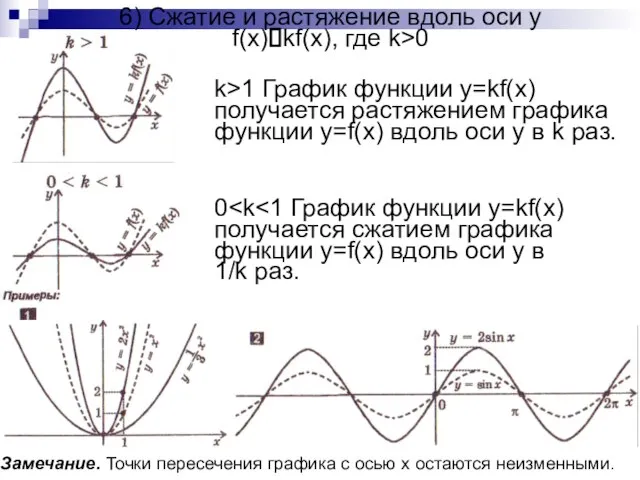
- 9. 6) Сжатие и растяжение вдоль оси y f(x)?kf(x), где k>0 k>1 График функции y=kf(x) получается растяжением
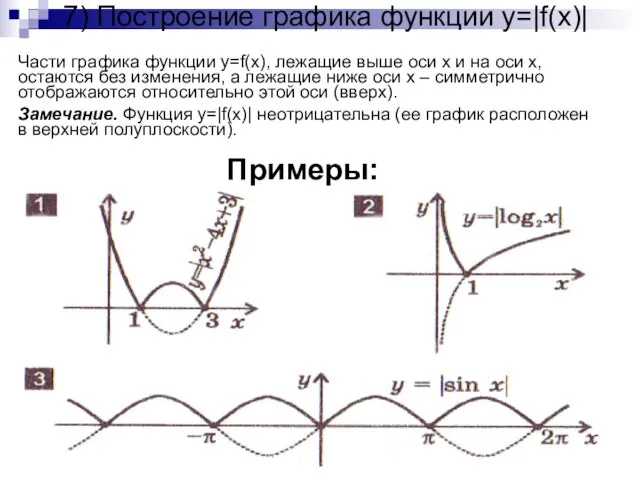
- 10. 7) Построение графика функции y=|f(x)| Части графика функции y=f(x), лежащие выше оси x и на оси
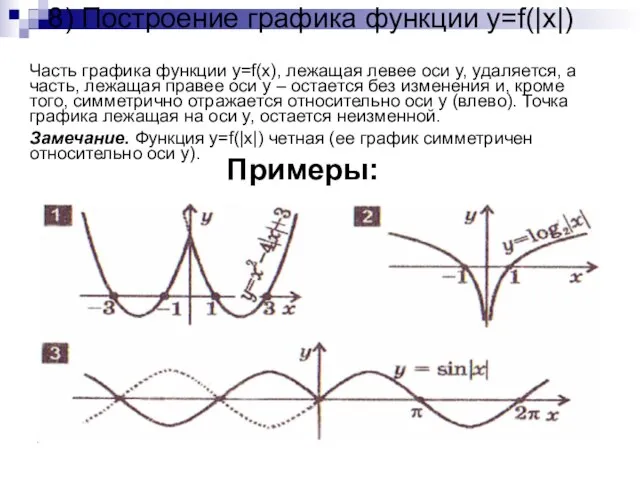
- 11. 8) Построение графика функции y=f(|x|) Часть графика функции y=f(x), лежащая левее оси y, удаляется, а часть,
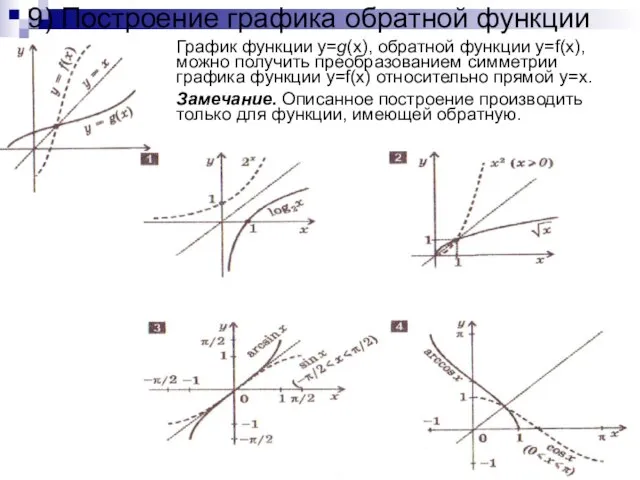
- 12. 9) Построение графика обратной функции График функции y=g(x), обратной функции y=f(x), можно получить преобразованием симметрии графика
- 13. Построение графиков сложных функций с помощью последовательных преобразований графиков элементарных функций (на примерах)
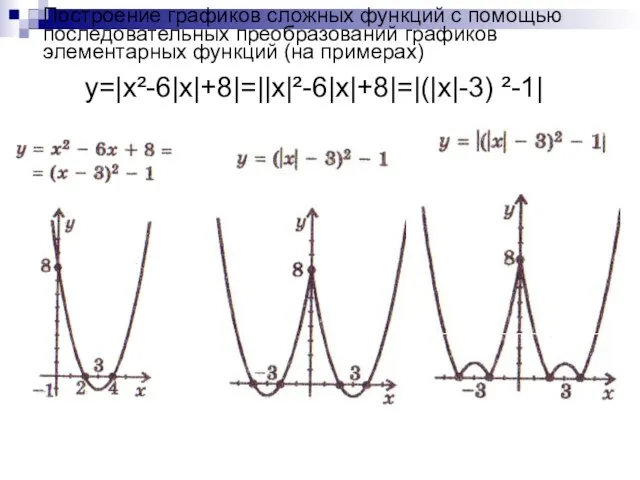
- 14. Построение графиков сложных функций с помощью последовательных преобразований графиков элементарных функций (на примерах) y=|x²-6|x|+8|=||x|²-6|x|+8|=|(|x|-3) ²-1|
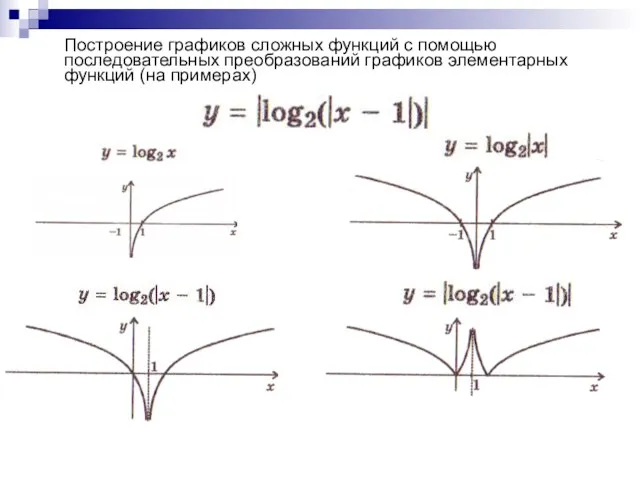
- 15. Построение графиков сложных функций с помощью последовательных преобразований графиков элементарных функций (на примерах)
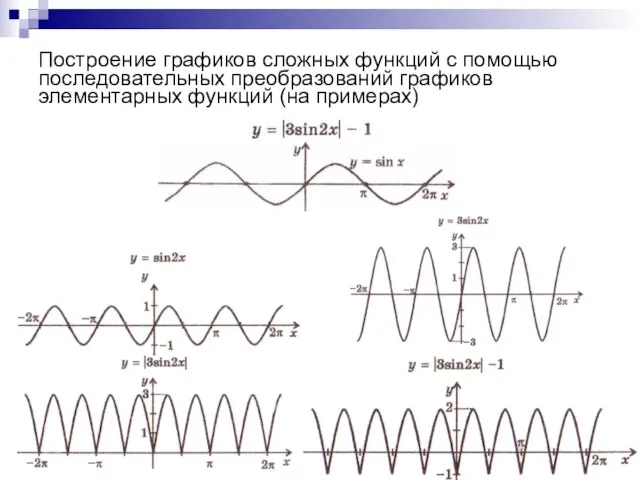
- 16. Построение графиков сложных функций с помощью последовательных преобразований графиков элементарных функций (на примерах)
- 17. Применение правил преобразования графиков при решении заданий ЕГЭ (части C).
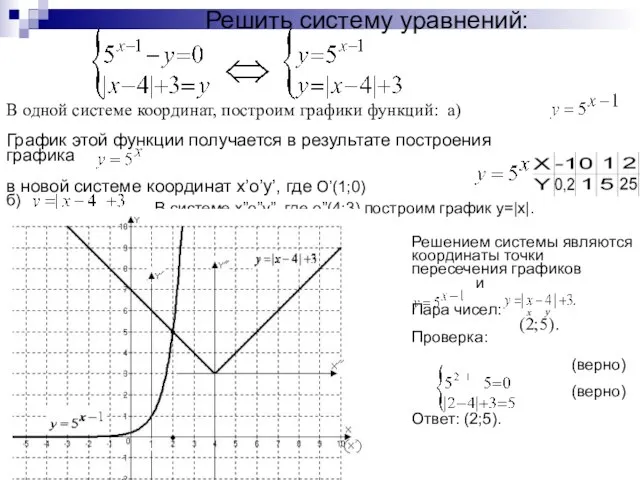
- 18. Решить систему уравнений: В одной системе координат, построим графики функций: а) График этой функции получается в
- 19. Решить уравнение: f(g(x))+g(f(x))=32, если известно, что и Решение: Преобразуем функцию f(x). Так как , то Тогда
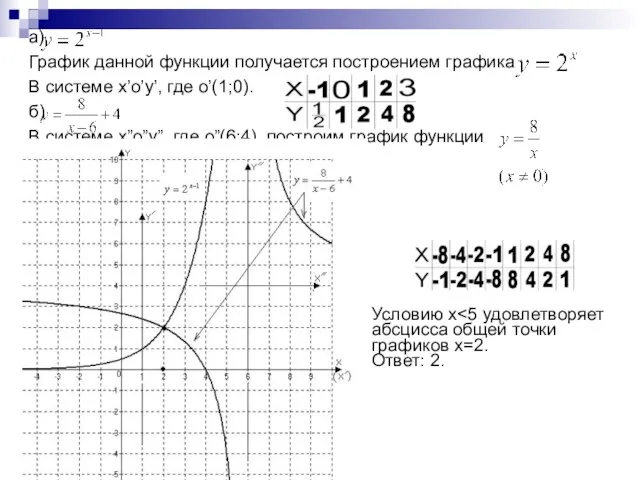
- 20. а) График данной функции получается построением графика В системе x’o’y’, где o’(1;0). б) В системе x”o”y”,
- 21. Вывод: Мы видим, что правила преобразования графиков существенно упрощают построение графиков сложных функций. Помогают найти нетрадиционное
- 23. Скачать презентацию






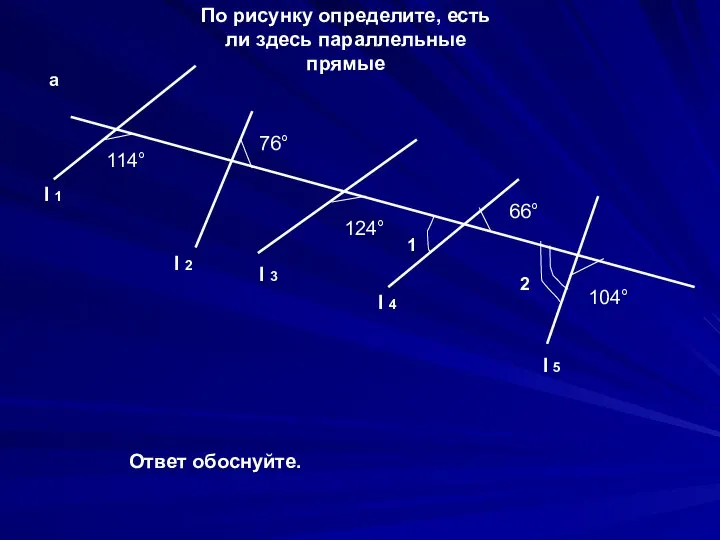 Параллельные прямые
Параллельные прямые Построение желаемой ЛАЧХ разомкнутой системы в частотном методе синтеза корректирующего звена
Построение желаемой ЛАЧХ разомкнутой системы в частотном методе синтеза корректирующего звена Деление с остатком
Деление с остатком Деление на трехзначное число
Деление на трехзначное число Решение тригонометрических уравнений
Решение тригонометрических уравнений Распределительное свойство умножения
Распределительное свойство умножения Несобственные интегралы. Геометрические приложения определенного интеграла
Несобственные интегралы. Геометрические приложения определенного интеграла Основные постулаты
Основные постулаты Тренажёр. Таблица умножения
Тренажёр. Таблица умножения Одночлены. Обобщающий урок
Одночлены. Обобщающий урок Параллельное и последовательное соединения
Параллельное и последовательное соединения Презентация на тему Расстояние от точки до прямой
Презентация на тему Расстояние от точки до прямой  Таблица умножения на 3
Таблица умножения на 3 Математика. Числа до 20
Математика. Числа до 20 Как построить график функции y=f(x)+m, если известен график функции y=f(x)
Как построить график функции y=f(x)+m, если известен график функции y=f(x) Час занимательной математики. 5 класс
Час занимательной математики. 5 класс Математические ребусы
Математические ребусы Определение стоимости проезда пассажира на железнодорожном транспорте. Задания
Определение стоимости проезда пассажира на железнодорожном транспорте. Задания Решение задач по теме Параллелограмм
Решение задач по теме Параллелограмм Степень числа
Степень числа Свойства параллельных плоскостей (10 класс)
Свойства параллельных плоскостей (10 класс) Два обыкновенных дифференциальных уравнения
Два обыкновенных дифференциальных уравнения Дифференциальное исчисление
Дифференциальное исчисление Жили-были числа
Жили-были числа Цифра 3
Цифра 3 Геометрия вокруг нас
Геометрия вокруг нас Матрицы. Основные понятия
Матрицы. Основные понятия Аксиомы стереометрии и их следствия
Аксиомы стереометрии и их следствия