Содержание
- 2. Цель: научиться применять на практике две новые формулы сокращенного умножения.
- 3. x2+y2+2xy c2d2+k2-2cdk 4a2+9b2+12ab Продолжаем учиться читать. полные квадраты x2+y2+xy c2d2+k2-cdk 4a2+9b2+ab. неполные квадраты Сравни!
- 4. Прочитайте выражение (x-y)(x2+y2+xy)= (x+y)(x2+y2-xy)= =x3-y3 =x3+y3 Произведение разности двух выражений на неполный квадрат суммы равно разности
- 5. (0,2a+0,5b)(0,04a2+0,25b2-0,1ab)= (25f4+4z2+10f2z)(5f2-2z)= (c2-1/2y)(c4+1/2y2+c2y)= (cd+k)(c2d2+k2-cdk)= (a-b)(a2+b2+ab)= (3+12y3)(9+144y6+36y3)= (4/9x10+36x2 +8x6)(2/3x5-6x)= Применим теорию на практике a3-b3 (cd)3+k3=с3d3+k3 (c2)3-(1/2y)3=c6-1/8y3 (5f2)3-(2z)3=125f6-8z3
- 6. Доверяй, но проверяй!
- 8. Скачать презентацию





 Зачем нужна математика
Зачем нужна математика Степень с отрицательным показателем
Степень с отрицательным показателем Презентация на тему Алгебра и начала математического анализа
Презентация на тему Алгебра и начала математического анализа  Презентация по математике "Переместительное свойство сложения" -
Презентация по математике "Переместительное свойство сложения" -  Погрешности измерений
Погрешности измерений Волшебная страна - Геометрия
Волшебная страна - Геометрия Линейная презентация
Линейная презентация Переместительный и сочетательный законы сложения
Переместительный и сочетательный законы сложения Производная частного двух функций
Производная частного двух функций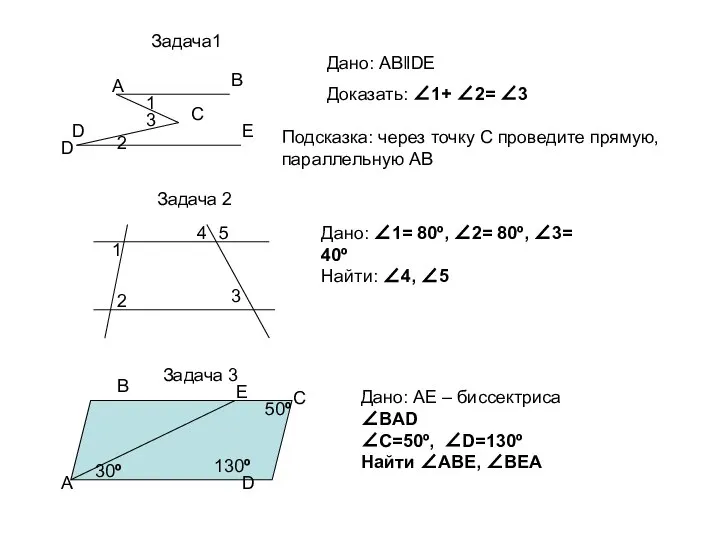 Параллельные прямые (тест)
Параллельные прямые (тест) MV1_Lektsia_2_-_Predstavlenie_nechetkikh_znaniy_-_kopia
MV1_Lektsia_2_-_Predstavlenie_nechetkikh_znaniy_-_kopia Пифагор и его школа
Пифагор и его школа 27.09 Графики функций
27.09 Графики функций Задачи на вычисление площадей и объемов тел вращения и многогранников
Задачи на вычисление площадей и объемов тел вращения и многогранников Декартова прямоугольная система координат на плоскости
Декартова прямоугольная система координат на плоскости Равенство углов наложением
Равенство углов наложением Самостоятельная работа по математике
Самостоятельная работа по математике Презентация на тему Преобразование графиков. Тригонометрические функции. Алгебра и начала анализа. 10 класс
Презентация на тему Преобразование графиков. Тригонометрические функции. Алгебра и начала анализа. 10 класс  Математическое путешествие (1 урок)
Математическое путешествие (1 урок) Тест для учащихся 1 класса
Тест для учащихся 1 класса Задачи на вычисление площади боковой поверхности циллиндра
Задачи на вычисление площади боковой поверхности циллиндра Форматы вывода результата вычислений и логические операции в MATLAB
Форматы вывода результата вычислений и логические операции в MATLAB Презентация на тему Куб
Презентация на тему Куб  Сообщение по истории математики «Из истории позиционных систем счисления» Выполнила ученица 6 «А класса» Дивии Идегел
Сообщение по истории математики «Из истории позиционных систем счисления» Выполнила ученица 6 «А класса» Дивии Идегел Решение уравнений на нахождение слагаемого
Решение уравнений на нахождение слагаемого Повторение курса алгебры (7 класс)
Повторение курса алгебры (7 класс) Теорема Пифагора
Теорема Пифагора Расстояние между скрещивающимися прямыми
Расстояние между скрещивающимися прямыми