Содержание
- 2. §1. МНОЖЕСТВА ►Множество это совокупность (собрание, класс, семейство...) некоторых объектов, объединенных по какому-либо признаку. ►Объекты, образующие
- 3. ►Множество, не содержащее ни одного элемента, называется пустым, обозначается символом Ø. ► множество А называется подмножеством
- 4. ►Множества, элементами которых являются числа, называются числовыми. Примерами числовых множеств являются: N={1; 2; 3; ...; n;
- 5. Множество R содержит рациональные и иррациональные числа. Между этими множествами существует соотношение N ⊂ Zo ⊂
- 6. Пусть a и b—действительные числа, причем a ►Числовыми промежутками (интервалами) называют подмножества всех действительных чисел, имеющих
- 7. Пусть х0—любое действительное число (точка на числовой прямой). В частности, интервал (х0-ε,х0+ε), где ε > 0,
- 8. §2. ФУНКЦИЯ Одним из основных математических понятий является понятие функции. Понятие функции связано с установлением зависимости
- 9. ►х называется независимой переменной или аргументом, у называется зависимой переменной. Пример. x2+y2=9, x2-y2=1, y2=8x.
- 10. Пусть задана функция у=ƒ(х). 2.2 Числовые функции. График функции. Способы задания функций ►Графиком функции у=f(х) называется
- 11. Наиболее часто встречаются три способа задания функции: аналитический, табличный, графический. Аналитический способ: функция задается в виде
- 12. Графический способ: задается график функции. Значения функции у, соответствующие тем или иным значениям аргумента х, непосредственно
- 13. Табличный способ: функция задается таблицей ряда значений аргумента и соответствующих значений функции. Например, известные таблицы значений
- 14. 1. Четность и нечетность функции. ►Функция у=ƒ(х), заданная на множестве Х, называется четной(нечетной) , если выполнены
- 15. Пример • у=sinx, у=х3 — нечетные функции;
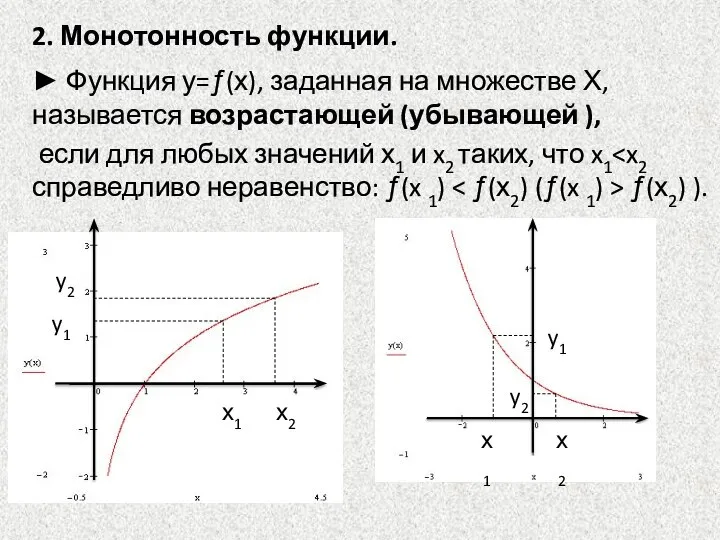
- 16. 2. Монотонность функции. ► Функция у=ƒ(х), заданная на множестве Х, называется возрастающей (убывающей ), если для
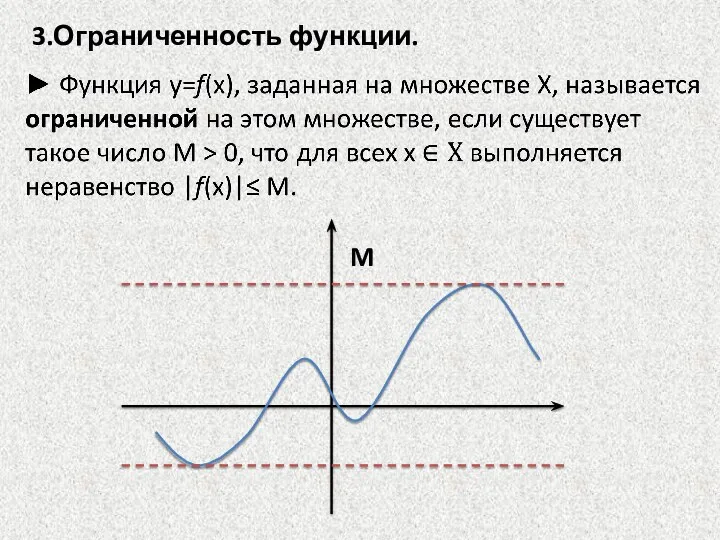
- 17. 3.Ограниченность функции.
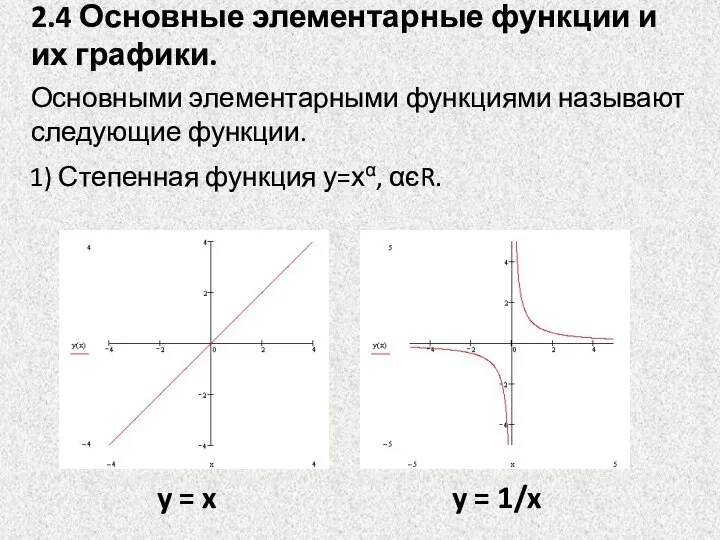
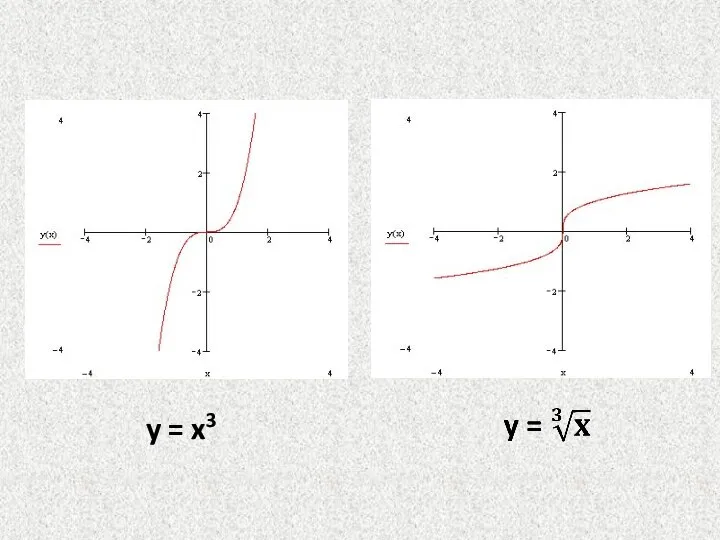
- 18. Основными элементарными функциями называют следующие функции. 2.4 Основные элементарные функции и их графики. 1) Степенная функция
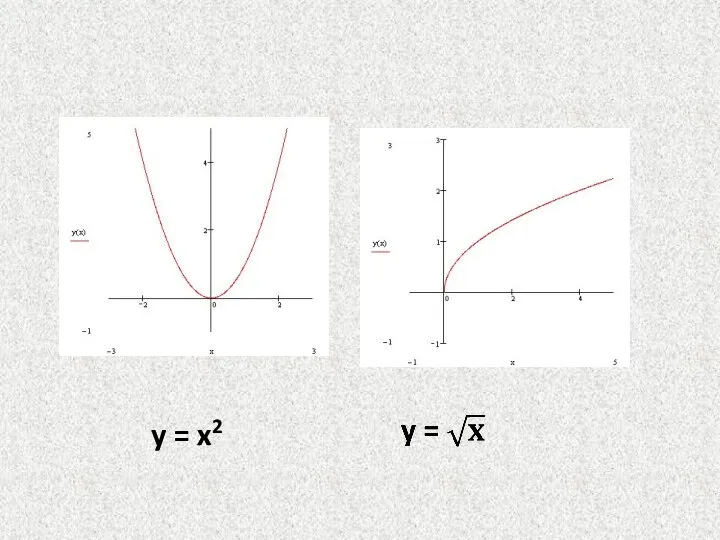
- 19. y = x2
- 20. y = x3
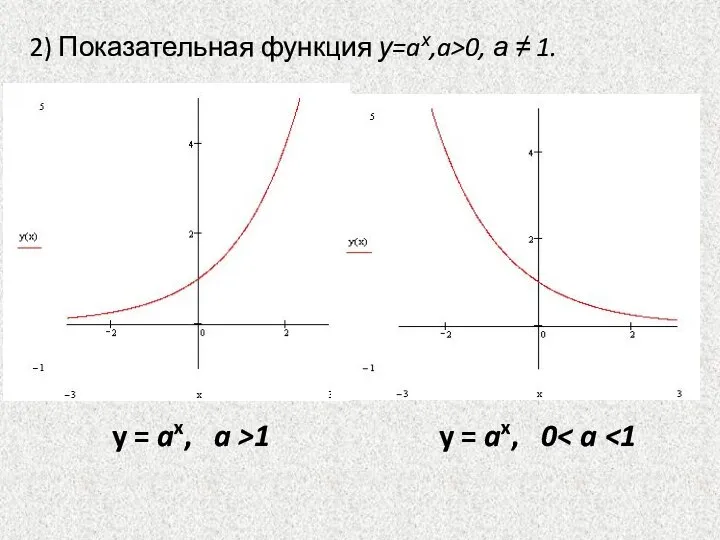
- 21. 2) Показательная функция у=aх,a>0, а ≠ 1. y = ax, a >1 y = ax, 0
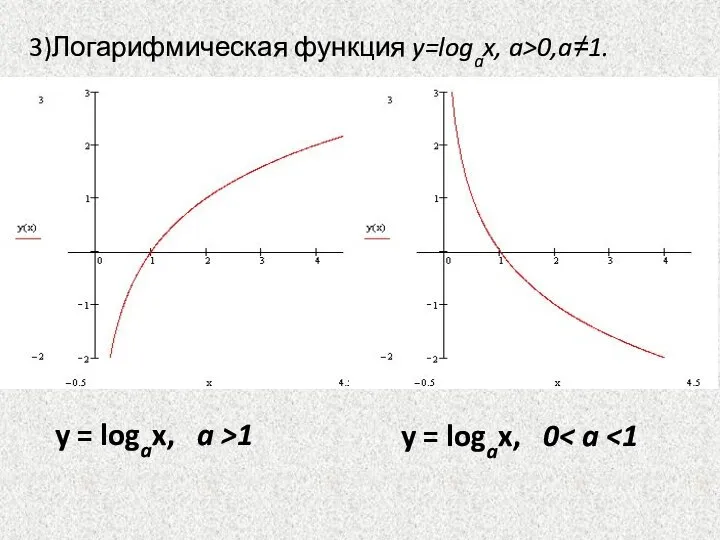
- 22. 3)Логарифмическая функция y=logax, a>0,a≠1. y = logax, a >1 y = logax, 0
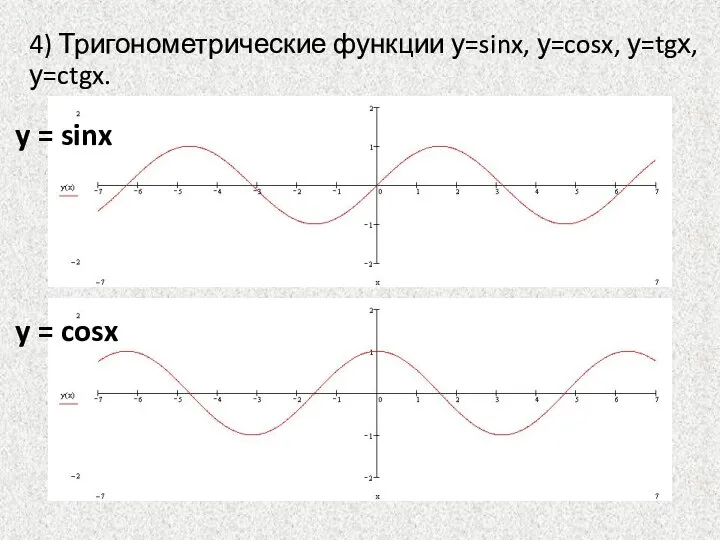
- 23. 4) Тригонометрические функции у=sinx, у=cosx, у=tgх, у=ctgx. y = cosx y = sinx
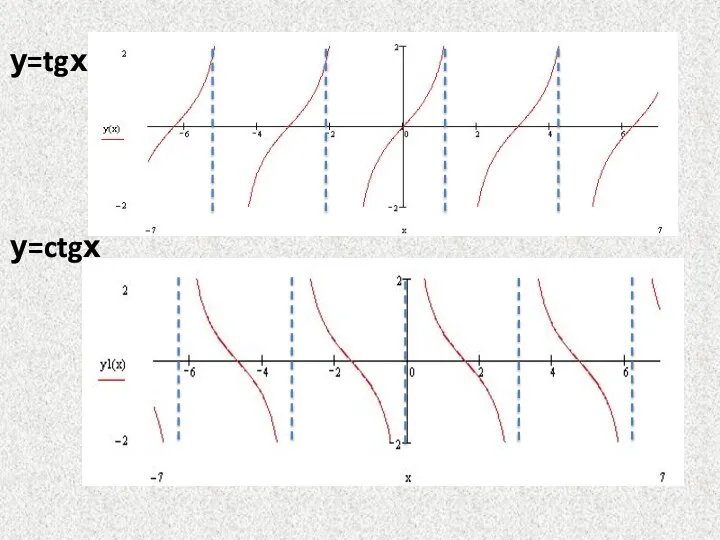
- 24. у=tgх у=ctgх
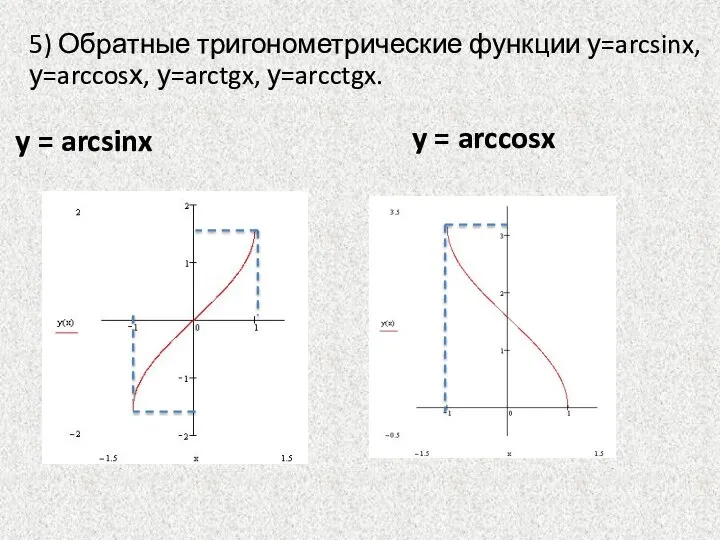
- 25. 5) Обратные тригонометрические функции у=arcsinx, у=arccosх, у=arctgx, у=arcctgx. y = arcsinx y = arccosx
- 27. Скачать презентацию














 Решение задач по теме: Двумерный массив. Профильный уровень
Решение задач по теме: Двумерный массив. Профильный уровень Свойства степени с натуральным показателем
Свойства степени с натуральным показателем Тригонометрия. Сумма и разность синуса, косинуса
Тригонометрия. Сумма и разность синуса, косинуса Дифференциальное исчисление функции одной переменной
Дифференциальное исчисление функции одной переменной Арифметичская прогрессия
Арифметичская прогрессия Золотое сечение
Золотое сечение Конструктивная геометрия. Лекция 5. Метрические задачи
Конструктивная геометрия. Лекция 5. Метрические задачи Умножение многозначных чисел на однозначное и двузначное число. Урок – путешествие (закрепление) по математике, 4 класс Состави
Умножение многозначных чисел на однозначное и двузначное число. Урок – путешествие (закрепление) по математике, 4 класс Состави Приёмы устных вычислений вида: 470 + 80, 560 - 90
Приёмы устных вычислений вида: 470 + 80, 560 - 90 Оптимизация по методу Бокса-Уилсона
Оптимизация по методу Бокса-Уилсона Асимптотические методы. Граничные условия на горизонтальной скважине. (Лекция 3)
Асимптотические методы. Граничные условия на горизонтальной скважине. (Лекция 3) Сравнение моделей
Сравнение моделей Вторая производная, ее физический смысл. Применение производной к построению графиков функций
Вторая производная, ее физический смысл. Применение производной к построению графиков функций Занимательная математика
Занимательная математика Логарифмические неравенства
Логарифмические неравенства Содержание функциональной пропедевтики в начальной школе, 5–6-х классах, в начале курса алгебры
Содержание функциональной пропедевтики в начальной школе, 5–6-х классах, в начале курса алгебры Проверочная работа на конец первой четверти в 5 классе
Проверочная работа на конец первой четверти в 5 классе Несобственные интегралы
Несобственные интегралы Линейные уравнения
Линейные уравнения Считаем со смешариками. Тренажер Сложенеие и вычитание в пределах 10.Технологический прием Анимированная сорбонка
Считаем со смешариками. Тренажер Сложенеие и вычитание в пределах 10.Технологический прием Анимированная сорбонка Сокращение дробей. Графический диктант
Сокращение дробей. Графический диктант Однородные тригонометрические уравнения
Однородные тригонометрические уравнения Несложная тригонометрия
Несложная тригонометрия Complete each of the following:
Complete each of the following: Круговая окружность
Круговая окружность Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика Теорема Пифагора
Теорема Пифагора Матрицы и действия над ними
Матрицы и действия над ними