Содержание
- 2. Цель: закрепляем умение видеть в предложенных выражениях формулы; учимся применять полученные умения при решении различных математических
- 3. Итак, повторим…
- 4. Квадрат суммы (разности). (a±b)2=a2+b2±2ab Квадрат суммы (разности) двух выражений равен сумме квадратов этих выражений плюс (минус)
- 5. Произведение разности двух выражений на их сумму равно… (a-b)(a+b)= a2-b2 …разности квадратов этих выражений.
- 6. Прочитайте выражение (x-y)(x2+y2+xy)= (x+y)(x2+y2-xy)= =x3-y3 =x3+y3 Произведение разности двух выражений на неполный квадрат суммы равно разности
- 7. x2+ * +2xy (x + * )2= ( * - k)2= 4d2+k2- * (x + *
- 8. Практикум №№ 897, 904, 905, 906 (а)
- 9. Практикум № 897 В левой части видим произведение разности двух выражений на неполный квадрат суммы (разность
- 10. Практикум № 904 Предложенная запись диктует нам возведение в квадрат сначала разности, потом суммы, затем умножение
- 11. Практикум № 905 Первые два множителя представляют собой произведение…. (x -у )(х+у)(х2+у2)= =(x2-у2)(х2+у2)= x4-у4
- 12. Практикум № 906 Можно, конечно, выполнить все действия так как они предложены в записи и это
- 13. Самостоятельная работа. 1 в. 2 в. №1 Упростите выражение и найдите его значение: (5x+4)(25x2-20x+16)-64, при х=2.
- 14. Проверь себя. №1 (5x+4)(25x2-20x+16)-64= =(125х3+64)-64=125х3. При х=2; 125х3=125.8=1000 №1 (2а-b)(4a2+2ab+b2)+b3= =(8a3-b3)+b3=8a3 . При a=-2; b=1; 8a3=8.(-8)=-64
- 15. Проверь себя. 1 в. 2 в. №3 (2х+3)2-7х=(2х-1)(2х+1) 4х2+9+12х-7x=4х2-1 4х2-4х2+12х-7x=-9-1 5х=-10 х=-2 №3 (x-4)(x+4)-6х=(х-2)2 x2-16-6x=x2+4-4x x2-x2+4x-6x=16+4
- 17. Скачать презентацию














 2.МатСтатистика-Критерии и Различия
2.МатСтатистика-Критерии и Различия Вычисление значений числовых выражений с действиями разной степени. Проверка деления умножением. 3 класс
Вычисление значений числовых выражений с действиями разной степени. Проверка деления умножением. 3 класс Презентация на тему Готфрид Вильгельм Лейбниц
Презентация на тему Готфрид Вильгельм Лейбниц  Графический диктант. Тема: Делимость чисел
Графический диктант. Тема: Делимость чисел Практическое применение площадей геометрических фигур
Практическое применение площадей геометрических фигур Государственное общеобразовательное учреждение Гимназия№49 Приморского района Санкт -Петербурга «Путешествие Алисы в страну Ма
Государственное общеобразовательное учреждение Гимназия№49 Приморского района Санкт -Петербурга «Путешествие Алисы в страну Ма Площади геометрических фигур
Площади геометрических фигур Презентация на тему Свойства степени с натуральным показателем
Презентация на тему Свойства степени с натуральным показателем  Инфекционные заболевания, их классификация и профилактика
Инфекционные заболевания, их классификация и профилактика pril1
pril1 Серединный перпендикуляр
Серединный перпендикуляр Вычисление углов между прямыми и плоскостями
Вычисление углов между прямыми и плоскостями Число или цифра 3
Число или цифра 3 Турнир знаний. Что это за формула
Турнир знаний. Что это за формула Задачи про виноград и изюм
Задачи про виноград и изюм Презентация на тему Параллельный перенос и Поворот
Презентация на тему Параллельный перенос и Поворот  Решение задач. Параллельные прямые
Решение задач. Параллельные прямые Тест по теме: Углы. Параллельные прямые. Перпендикулярные прямые
Тест по теме: Углы. Параллельные прямые. Перпендикулярные прямые Решение задач на проценты
Решение задач на проценты Факториал. Теорема
Факториал. Теорема Векторы. Действия с векторами
Векторы. Действия с векторами Применение теории паркета для доказательства свойств и признаков параллелограмма и трапеции
Применение теории паркета для доказательства свойств и признаков параллелограмма и трапеции Числовые ряды
Числовые ряды Текстовые задачи. Движение по кругу и по воде
Текстовые задачи. Движение по кругу и по воде Золотое сечение
Золотое сечение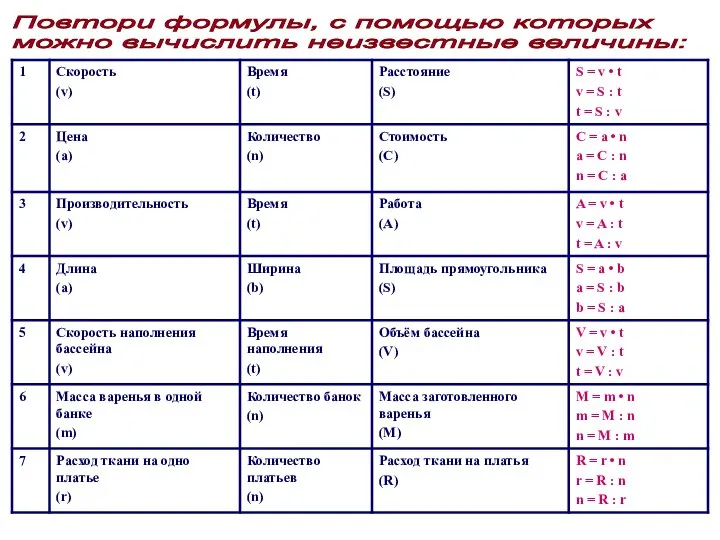 Скорость (v), Время (t), Расстояние (S)
Скорость (v), Время (t), Расстояние (S) Степенные ряды
Степенные ряды Задачи на проценты. Решения
Задачи на проценты. Решения