Содержание
- 2. Машина движется по шоссе с постоянной скоростью 70 км/ч. За время t ч машина проходит путь
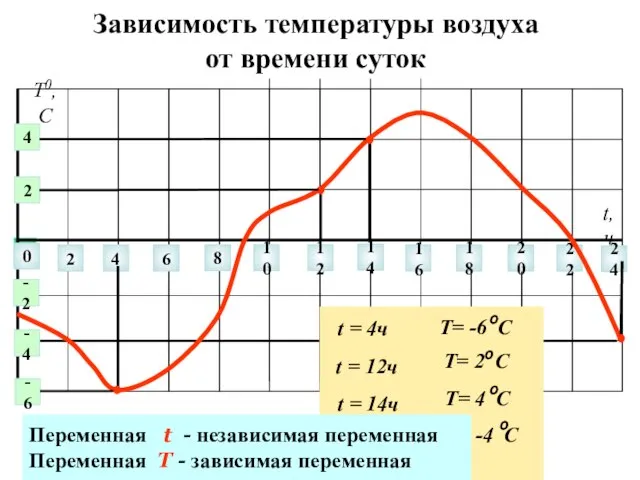
- 3. Зависимость температуры воздуха от времени суток 0 2 4 6 8 10 12 14 22 24
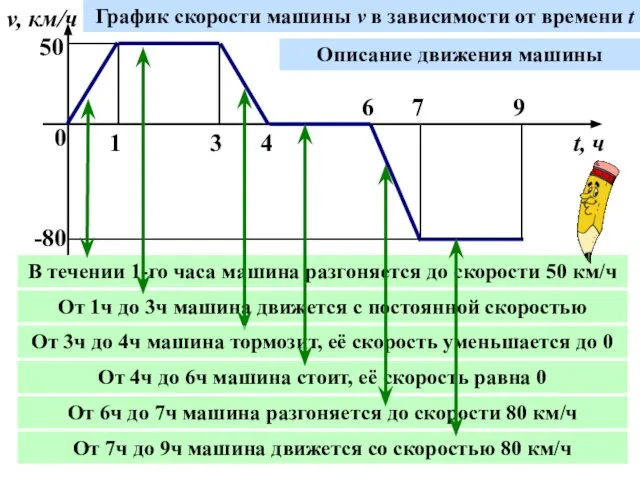
- 4. 0 1 3 4 6 7 9 v, км/ч t, ч 50 -80 График скорости машины
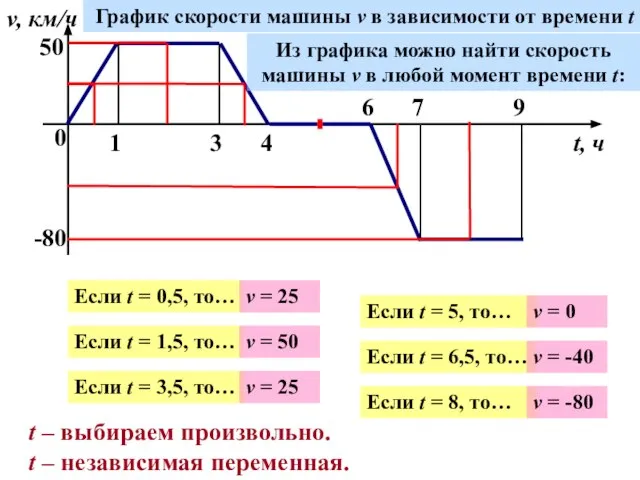
- 5. 0 1 3 4 6 7 9 v, км/ч t, ч 50 -80 График скорости машины
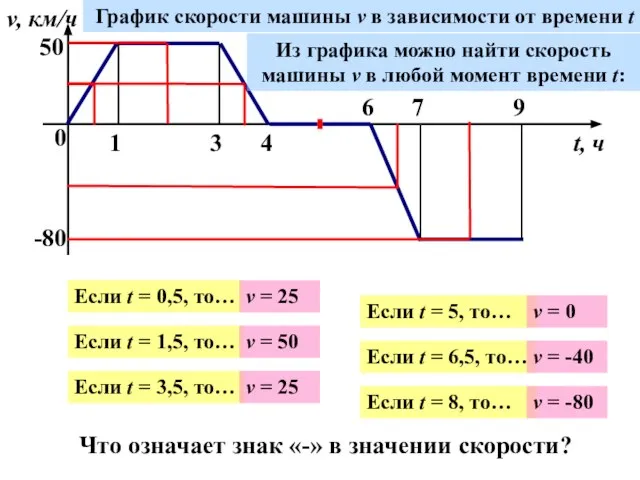
- 6. 0 1 3 4 6 7 9 v, км/ч t, ч 50 -80 График скорости машины
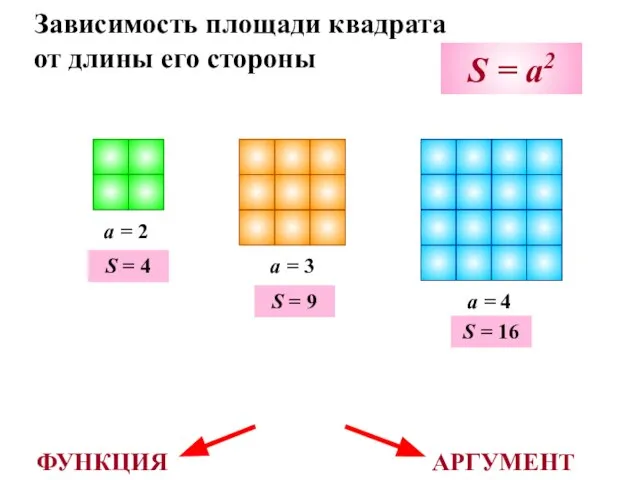
- 7. Зависимость площади квадрата от длины его стороны a = 2 a = 3 a = 4
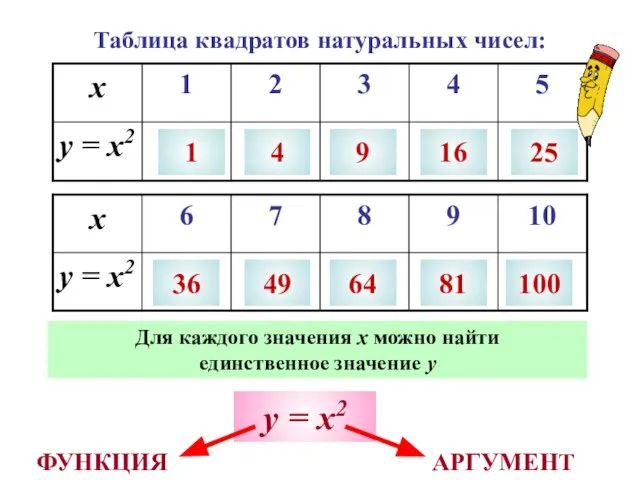
- 8. Таблица квадратов натуральных чисел: 1 4 9 16 25 36 49 64 81 100 Для каждого
- 9. В рассмотренных примерах каждому значению независимой переменной соответствует единственное значение зависимой переменной. Зависимость одной переменной от
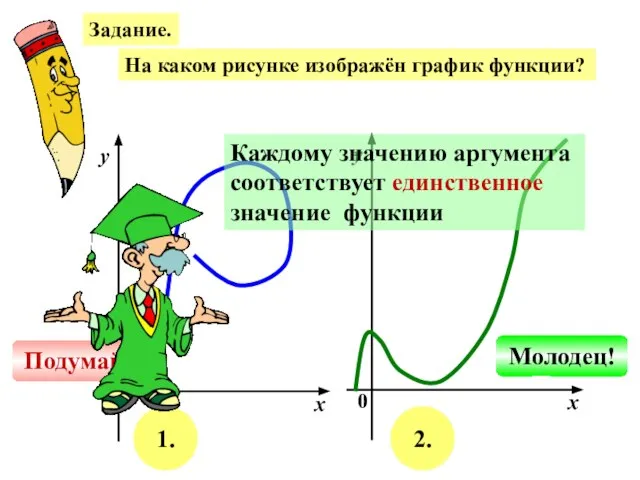
- 10. Задание. На каком рисунке изображён график функции? х у 0 х у 0 1. 2. Подумай!
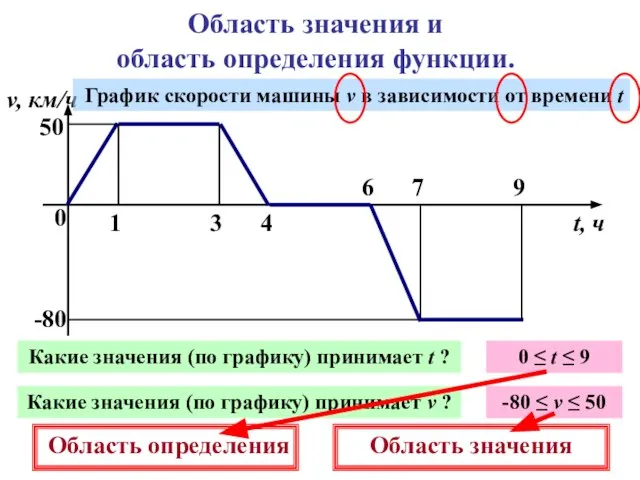
- 11. Область значения и область определения функции. 0 1 3 4 6 7 9 v, км/ч t,
- 12. Область значения и область определения функции. Машина движется по шоссе с постоянной скоростью 70 км/ч. За
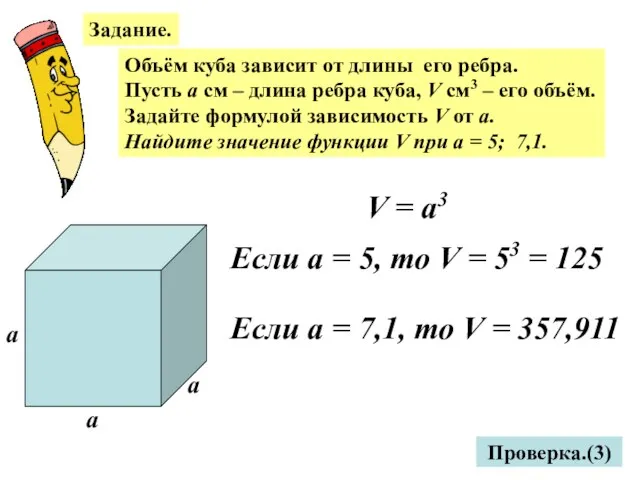
- 13. Задание. Объём куба зависит от длины его ребра. Пусть а см – длина ребра куба, V
- 14. Задание функции с помощью формулы. Формула позволяет для любого значения аргумента находить соответствующее значение функции путём
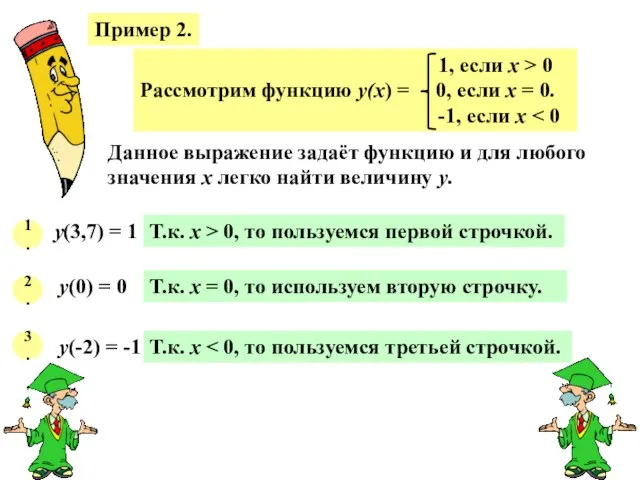
- 15. Пример 2. Данное выражение задаёт функцию и для любого значения х легко найти величину у. 1.
- 16. Пример 3. 1. В этом примере область определения указана – все значения х из промежутка 2
- 17. Задание. Найдите область определения функций: 1. 2. 3.
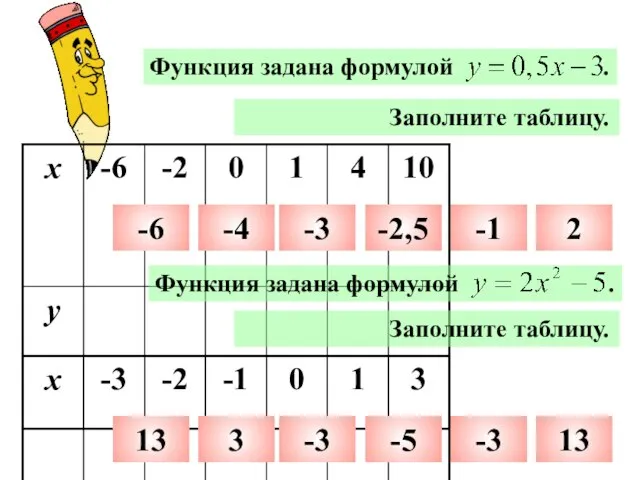
- 18. Функция задана формулой . Заполните таблицу. -6 -4 -3 -2,5 -1 2 Заполните таблицу. 13 3
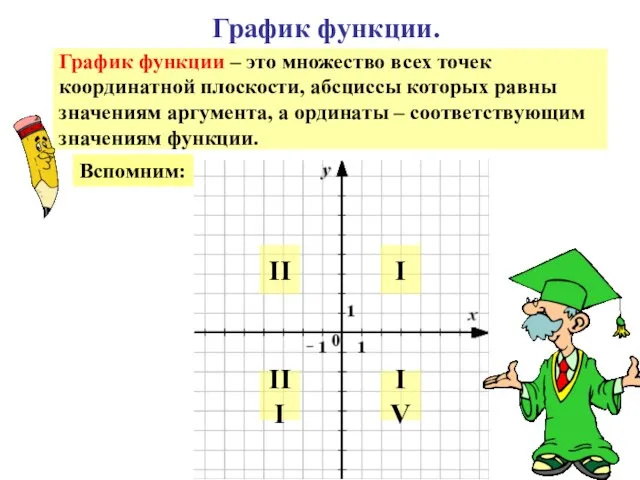
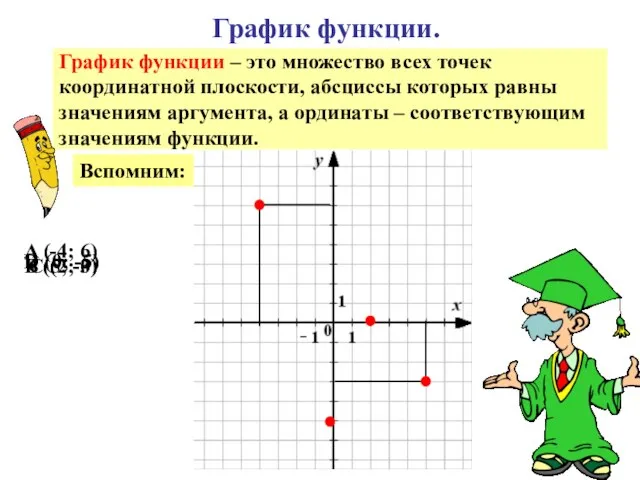
- 19. График функции. График функции – это множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента,
- 20. График функции. График функции – это множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента,
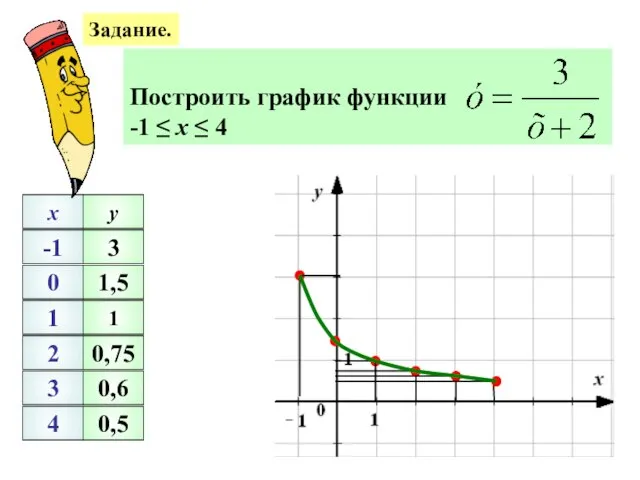
- 21. Задание. Построить график функции -1 ≤ х ≤ 4 -1 0 1 2 3 4 x
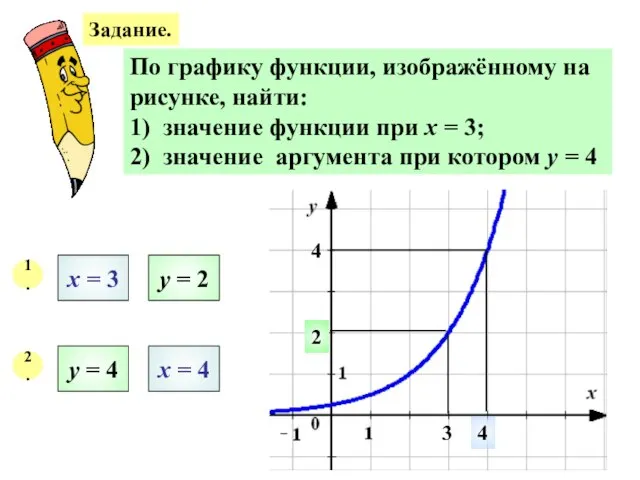
- 22. Задание. По графику функции, изображённому на рисунке, найти: 1) значение функции при х = 3; 2)
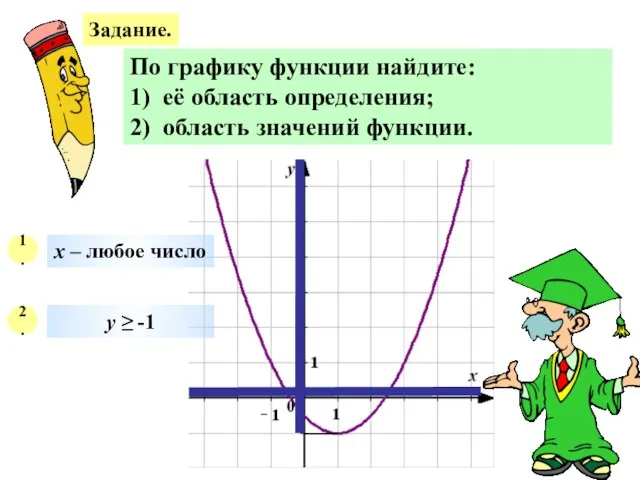
- 23. Задание. По графику функции найдите: 1) её область определения; 2) область значений функции. 1. х –
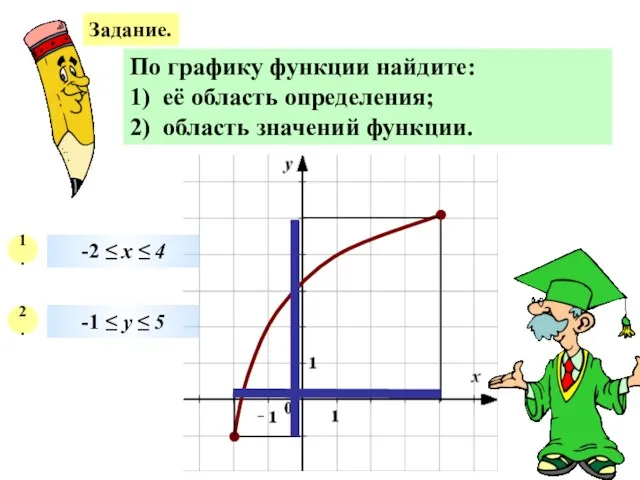
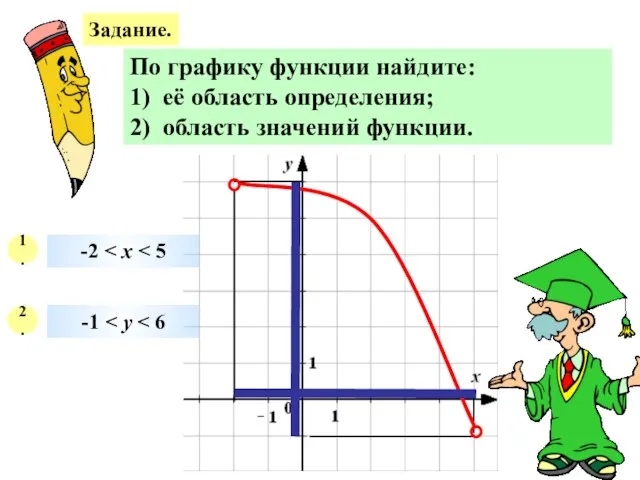
- 24. Задание. По графику функции найдите: 1) её область определения; 2) область значений функции. 1. 2. -2
- 25. Задание. По графику функции найдите: 1) её область определения; 2) область значений функции. 1. 2. -2
- 26. Спасибо за внимание!
- 28. Скачать презентацию







 Градиентные методы
Градиентные методы Пропорция – верное равенство двух отношений
Пропорция – верное равенство двух отношений Деление дробей
Деление дробей Решение прямоугольных треугольников
Решение прямоугольных треугольников Среднее арифметическое. Размах. Мода
Среднее арифметическое. Размах. Мода Деление с остатком. Решение задач
Деление с остатком. Решение задач Математика для анализа больших данных
Математика для анализа больших данных Презентация на тему Преобразование выражений содержащих квадратные корни
Презентация на тему Преобразование выражений содержащих квадратные корни  Элементы нелинейного функционального анализа. Гладкие многообразия. Способы задания атласа на окружности
Элементы нелинейного функционального анализа. Гладкие многообразия. Способы задания атласа на окружности Свойства монотонных функций
Свойства монотонных функций Презентация на тему Веселая математика 1 класс
Презентация на тему Веселая математика 1 класс  Закономерности построения формы изделия
Закономерности построения формы изделия Множества. Операции над множеством
Множества. Операции над множеством Z-преобразование. Лекция 4
Z-преобразование. Лекция 4 Мир многогранников
Мир многогранников Презентация на тему Вычисления с многозначными числами
Презентация на тему Вычисления с многозначными числами  Работа на повторение материала 6 класса
Работа на повторение материала 6 класса Вычисление определенных интегралов
Вычисление определенных интегралов Признаки возрастания и убывания функции
Признаки возрастания и убывания функции Движения
Движения Финансовая математика: банки, вклады, кредиты. Часть 2
Финансовая математика: банки, вклады, кредиты. Часть 2 Подготовка к ЕГЭ. Задача В7
Подготовка к ЕГЭ. Задача В7 Письменное умножение чисел, оканчивающихся нулями
Письменное умножение чисел, оканчивающихся нулями Методы решения тригонометрических уравнений
Методы решения тригонометрических уравнений Алгоритм умножения
Алгоритм умножения Презентация на тему Измерение углов
Презентация на тему Измерение углов  Смежные и вертикальные углы
Смежные и вертикальные углы Образование дробей. 5 класс
Образование дробей. 5 класс