Мир многогранников

Многогранники
Мы мирозданье многогранником зовём
И тщимся сосчитать бесчисленные грани,
Мы острые углы отыскиваем в нём –
И удивляемся бесплодности исканий.
Стремимся гранями разбить добро и зло,
Но смертный ум решений верных не находит;
Ведь если граней бесконечное число,
То в сферу многогранник переходит...
С.Дали
Выполнила: Выродова М.А.

Сегодняшний урок будет посвящен одному из увлекательных разделов геометрии– теории многогранников. Чем же привлекательны многогранники?
Они обладают богатой историей,которая связана с такими знаменитыми учеными древности,как Пифагор, Евклид, Архимед. Многогранники были известны в Древнем Египте и Вавилоне. В тоже время теория многогранников – современный раздел математики, имеющий практическое приложение в алгебре, теории чисел, в естествознании, в областях прикладной математики.
Математика, в частности геометрия, представляет собой могущественный инструмент преобразования мира, в котором по словам Готфрида Харби,
«нет места для некрасивой математики».
Выполнила: Выродова М.А.

Понятие многогранника является одним из центральных в курсе стереометрии
Многогранники как создания в природе красивы и симметричны.
Архимед
Выполнила: Выродова М.А.

Тетраэдр
Параллелепипед
Выполнила: Выродова М.А.

Многогранник - пространственная фигура, поверхность которой состоит из конечного числа многоугольников, называемых гранями многогранника. Стороны этих многоугольников называются ребрами многогранника, а вершины многоугольников –
вершинами многогранника.
Выполнила: Выродова М.А.

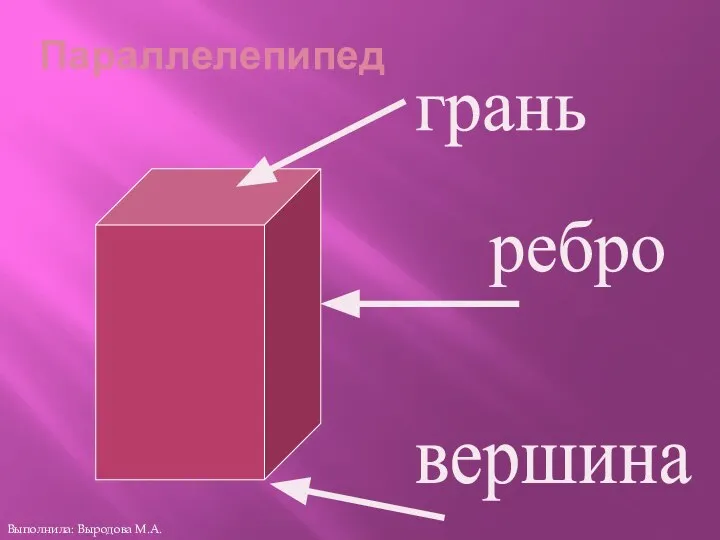
Параллелепипед
грань
ребро
вершина
Выполнила: Выродова М.А.

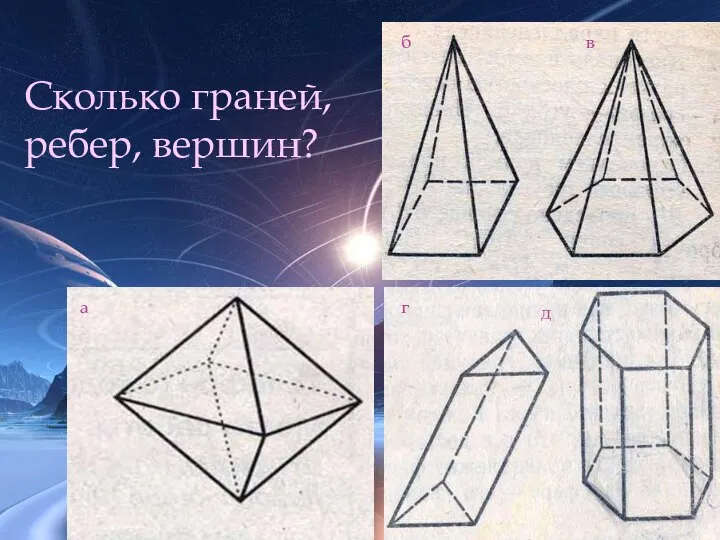
Сколько граней, ребер, вершин?
а
б
д
в
г
Выполнила: Выродова М.А.

Определение
Многогранник называется выпуклым, если он расположен по одну сторону от плоскости каждой его грани
Выполнила: Выродова М.А.

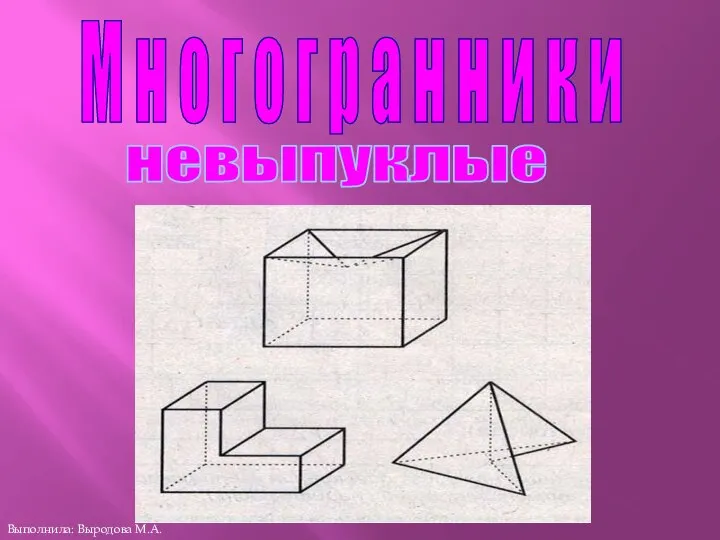
М н о г о г р а н н и к и
невыпуклые
Выполнила: Выродова М.А.

Утверждение
В выпуклом многограннике сумма всех плоских углов при каждой его вершине меньше 360°
Выполнила: Выродова М.А.

Разновидности
многогранников

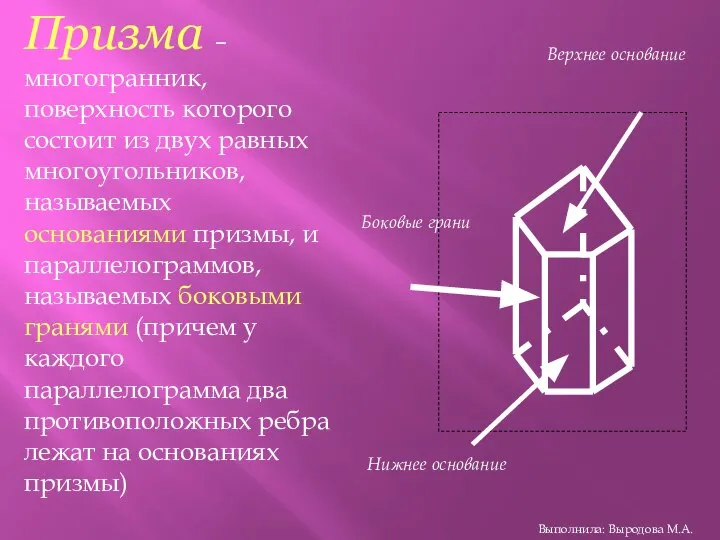
Призма – многогранник, поверхность которого состоит из двух равных многоугольников, называемых основаниями призмы, и параллелограммов, называемых боковыми гранями (причем у каждого параллелограмма два противоположных ребра лежат на основаниях призмы)
Верхнее основание
Нижнее основание
Выполнила: Выродова М.А.

Призма
«Призма есть телесная
фигура,заключенная между плоскостями,
из которых две противоположные равны
и параллельны, остальные же – параллелограммы»
Евклид
Выполнила: Выродова М.А.

Евклид ( предположительно 330- 277 до н.э. ) – математик Александрийской школы Древней Греции, автор первого дошедшего до нас трактата по математике «Начала» (в 15 книгах )
Выполнила: Выродова М.А.

В 18 веке Тейлор дал такое определение призмы:
«Призма - это многогранник,
у которого все грани, кроме двух,
параллельны одной прямой»
Выполнила: Выродова М.А.

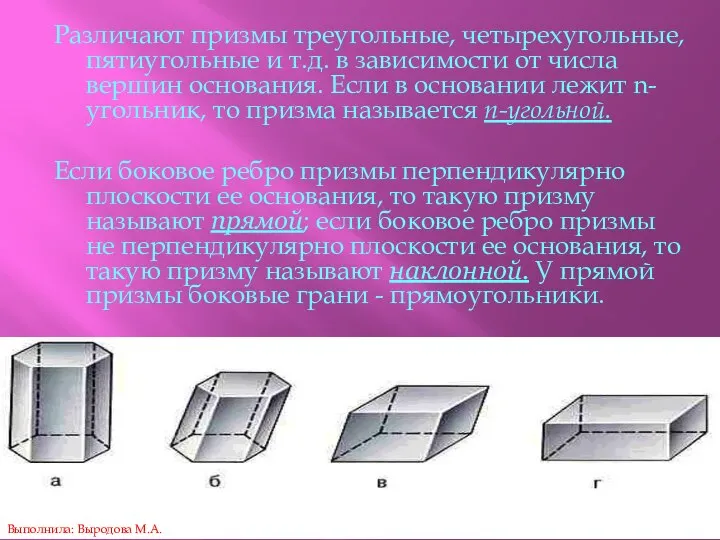
Различают призмы треугольные, четырехугольные, пятиугольные и т.д. в зависимости от числа вершин основания. Если в основании лежит n-угольник, то призма называется n-угольной.
Если боковое ребро призмы перпендикулярно плоскости ее основания, то такую призму называют прямой; если боковое ребро призмы не перпендикулярно плоскости ее основания, то такую призму называют наклонной. У прямой призмы боковые грани - прямоугольники.
Выполнила: Выродова М.А.

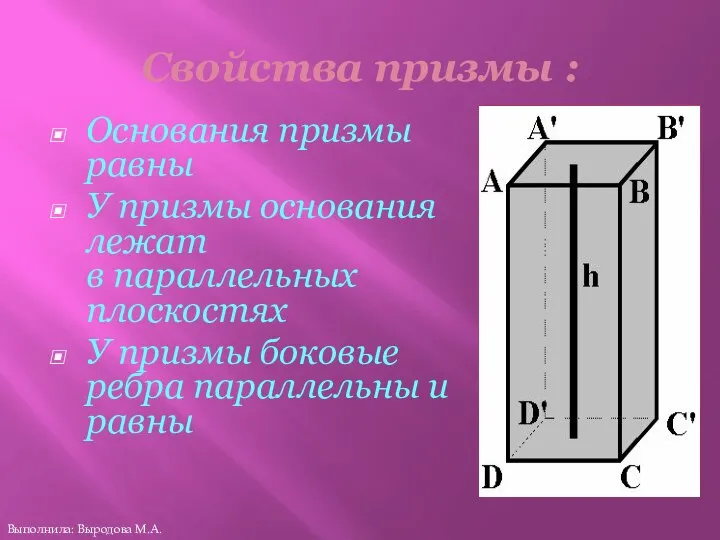
Свойства призмы :
Основания призмы равны
У призмы основания лежат
в параллельных плоскостях
У призмы боковые ребра параллельны и равны
Выполнила: Выродова М.А.

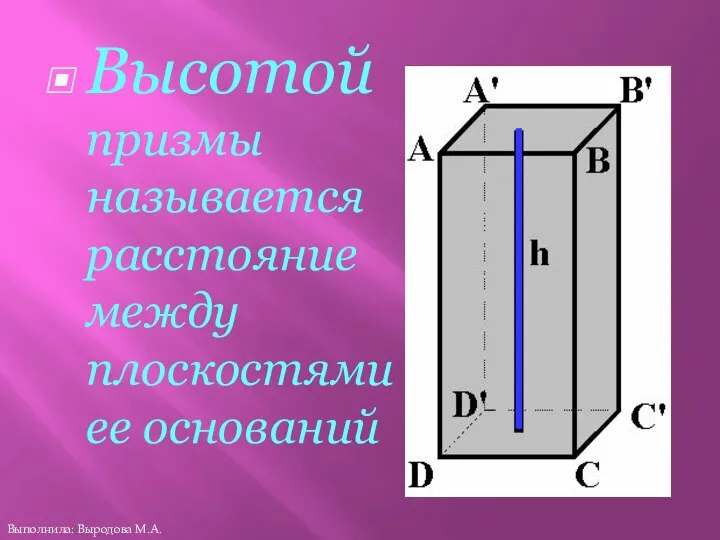
Высотой призмы называется расстояние между плоскостями ее оснований
Выполнила: Выродова М.А.

Оказывается, что призма может быть не только геометрическим телом, но
и художественным шедевром. Именно призма стала основой картин Пикассо, Брака, Грисса и т.д.
Кубизм
И н т е р е с н ы е ф а к т ы
Выполнила: Выродова М.А.

Оказывается, что снежинка может принять форму шестигранной призмы, но это будет зависеть от температуры воздуха
Ледяная призма
Выполнила: Выродова М.А.

В III веке до н. э. был построен маяк, чтобы корабли могли благополучно миновать рифы на пути в александрийскую бухту. Ночью им помогало в этом отражение языков пламени, а днём- столб дыма. Это был первый в мире маяк, и простоял он 1500 лет.
Маяк был построен на маленьком острове Фарос в Средиземном море, около берегов Александрии. На его строительство ушло 20 лет, а завершён он был около 280 года до н.э.
Александрийский маяк
Выполнила: Выродова М.А.

Маяк состоял из трёх мраморных башен, стоявших на основании из массивных каменных блоков. На вершине башни стояла статуя Зевса Спасителя. Общая высота маяка составляла 117 метров.
Огонь горел в верхней башне, которая формой напоминала цилиндр. За пламенем стояли бронзовые пластины, направляющие свет в море. С кораблей можно было видеть этот маяк на расстоянии до 50 км.
Выполнила: Выродова М.А.

Существуют не только геометрические формы, созданные руками человека. Их много и в самой природе. Воздействие на облик земной поверхности таких природных факторов, как ветер, вода, солнечный свет, весьма стихийно и носит беспорядочный характер. Однако песчаные дюны, галька на морском берегу, кратер потухшего вулкана имеют, как правило, геометрически правильные формы. В земле иногда находят камни такой формы, как будто их кто-то тщательно выпиливал, шлифовал, полировал. Это - кристаллы.
Выполнила: Выродова М.А.

Моделями прямой призмы служат :
классная комната
кирпич
спичечный коробок
Выполнила: Выродова М.А.

Оказывается, что кристаллы кальцита, сколько их не дроби на более мелкие части, всегда распадаются на осколки, имеющие форму параллелепипеда
Кристаллография
Выполнила: Выродова М.А.

Городские здания чаще всего имеют форму многогранников.
Как правило, это обычные параллелепипеды.
И лишь неожиданные архитектурные решения украшают города.
Выполнила: Выродова М.А.