Содержание
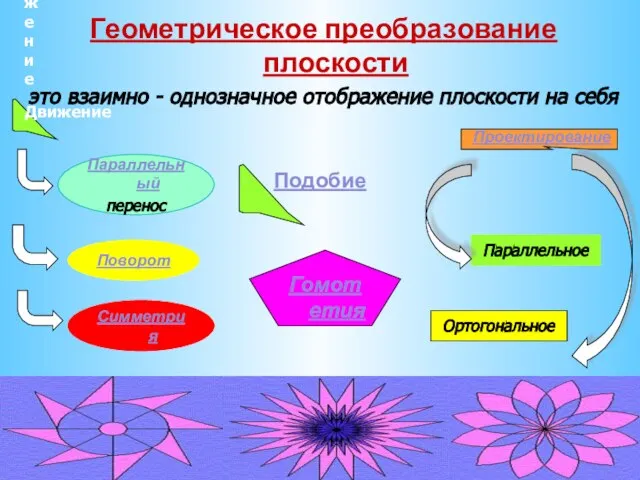
- 2. Движение Движение Подобие Параллельный перенос Поворот Симметрия Гомотетия Параллельное Ортогональное Геометрическое преобразование плоскости это взаимно -
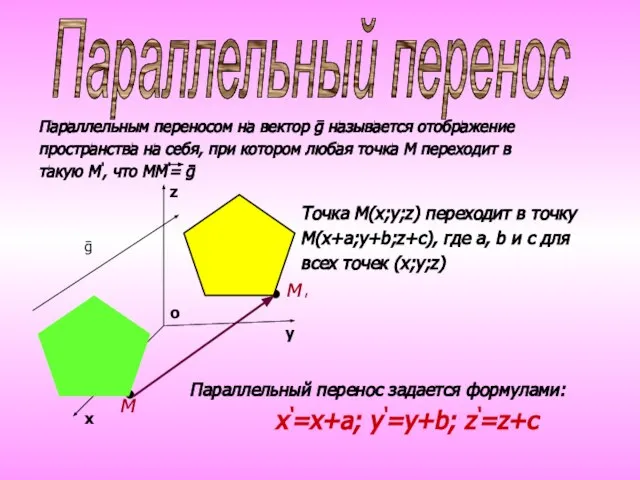
- 3. х у z о м м' • • Точка М(х;у;z) переходит в точку М(х+а;у+b;z+c), где а,
- 4. Параллельный перенос х у z о Параллельный перенос есть движение Движение, сохраняющее направление, является параллельным переносом
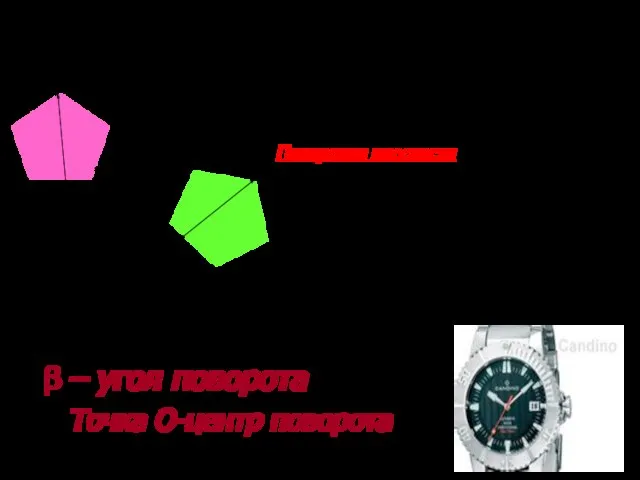
- 5. Поворотом плоскости около данной точки называется такое движение, при котором каждый луч, исходящий из этой точки,
- 6. Поворот в пространстве Спутники вращаются вокруг планет Планеты вращаются вокруг солнца
- 7. Вращение галактик в космосе
- 8. «Симметрия является той идеей, посредством которой человек на протяжении веков пытается постичь и создать порядок, красоту
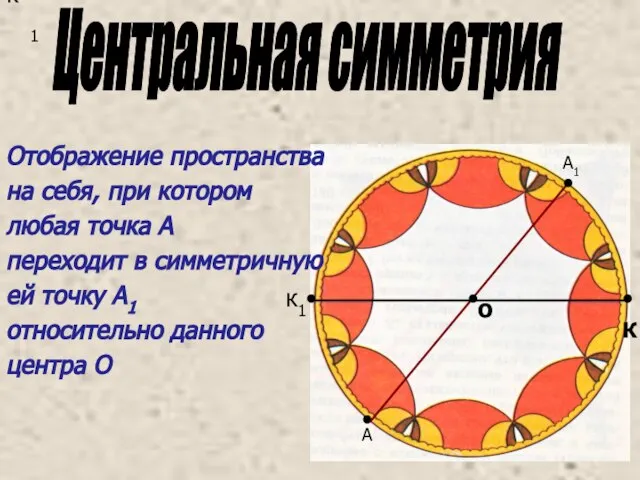
- 9. к1 к1 • • К А1 А • • Отображение пространства на себя, при котором любая
- 10. Применение центральной симметрии
- 11. Центральная симметрия в природе кактусы
- 12. Осевой симметрией с осью ℓ называется такое отображение пространства на себя, при котором любая точка М
- 13. Осевая симметрия в архитектуре Библиотека им. Лермонтова г. Ставрополь
- 14. Осевая симметрия храмов Церковь во имя апостола Андрея Первозванного г. Ставрополь. Церковь Андрея Первозванного. г. Ставрополь
- 15. Осевая симметрия Осевая симметрия животного мира
- 16. Осевая симметрия в природе
- 17. в в технике Осевая симметрия
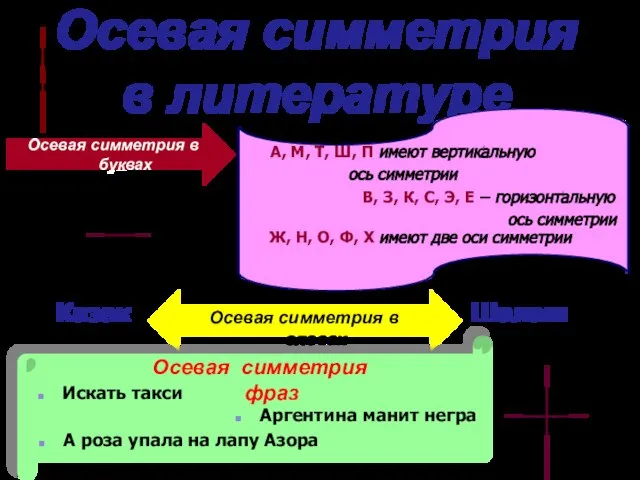
- 18. Осевая симметрия в литературе А Ж Э Осевая симметрия в буквах А, М, Т, Ш, П
- 19. Зеркальной симметрией(симметрией относительно плоскости) называется такое отображение пространства на себя, при котором любая точка Х переходит
- 20. З е р к а л ь н а я с и м м е т
- 21. Преобразование фигуры F в фигуру F‘ называется преобразованием подобия, если при этом преобразовании расстояние между точками
- 22. Гомотетией с центром О и коэффициентом k≠0 называется геометрическое преобразование, которое произвольно взятую точку А переводит
- 23. Кино в кинотеатрах
- 25. Скачать презентацию

















 Одночлены и их свойства. Тест
Одночлены и их свойства. Тест История системы мер длины (часть 2)
История системы мер длины (часть 2) Поверхностные интегралы первого рода
Поверхностные интегралы первого рода Актуализация знаний
Актуализация знаний Методы решения тригонометрических уравнений
Методы решения тригонометрических уравнений Пифагор Самосский
Пифагор Самосский Презентация на тему Внетабличное умножение и деление
Презентация на тему Внетабличное умножение и деление  Решение выражений в несколько действий
Решение выражений в несколько действий Презентация по математике "Письменные приёмы умножения" -
Презентация по математике "Письменные приёмы умножения" -  Интегрированный урок математики и чтения в 5 классе. Басни И.А.Крылова
Интегрированный урок математики и чтения в 5 классе. Басни И.А.Крылова Цифра 3. Урок математики в 1 классе
Цифра 3. Урок математики в 1 классе Осевая симметрия
Осевая симметрия Презентация на тему Раскрытие скобок (5 класс)
Презентация на тему Раскрытие скобок (5 класс)  Скалярное произведение в евклидовом и унитарном пространстве
Скалярное произведение в евклидовом и унитарном пространстве Теория пределов. Понятие предела. Предел функции в точке. Теоремы о пределах. Замечательные пределы. Бесконечно малые функции
Теория пределов. Понятие предела. Предел функции в точке. Теоремы о пределах. Замечательные пределы. Бесконечно малые функции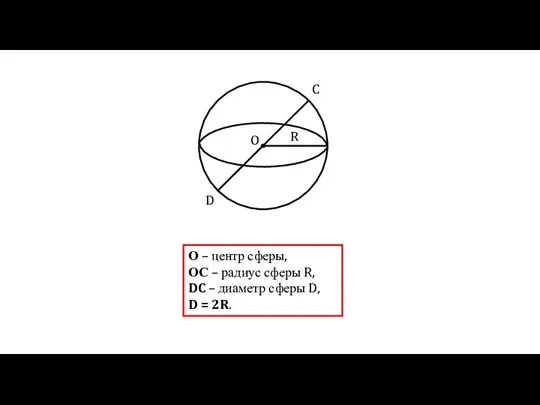 Уравнение сферы
Уравнение сферы 27.09 Графики функций
27.09 Графики функций Поворот. Пример построения треугольника
Поворот. Пример построения треугольника Алгоритм отыскания производной
Алгоритм отыскания производной Уравнения и неравенства
Уравнения и неравенства Приближённые значения чисел. Округление чисел
Приближённые значения чисел. Округление чисел Устный счёт
Устный счёт Функции и графики
Функции и графики Объём параллелепипеда. Задачи
Объём параллелепипеда. Задачи Великие математики древности. Архимед, Пифагор, Евклид, Фалес
Великие математики древности. Архимед, Пифагор, Евклид, Фалес Семинар по математике
Семинар по математике Вычисление производной
Вычисление производной Измерение углов без транспортира
Измерение углов без транспортира