Слайд 3Основные понятия
Осевая симметрия – тип симметрии, при которой каждой точке плоскости по

определенному закону ставится в соответствие другая точка той же плоскости.
Слайд 4Закон осевой симметрии
Точки M и M1 симметричны относительно прямой a, если a

– серединный перпендикуляр к отрезку MM1.
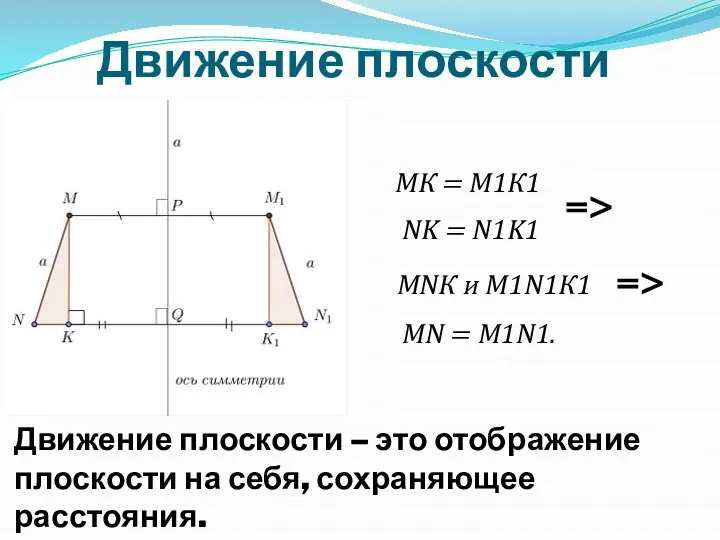
Слайд 5Движение плоскости
Движение плоскости – это отображение плоскости на себя, сохраняющее расстояния.
Слайд 6Задача 1
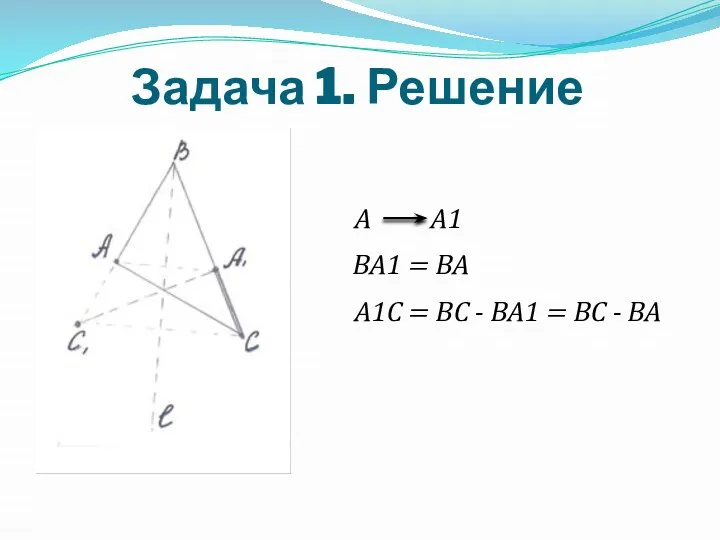
С помощью осевой симметрии постройте разность сторон ВС и ВА треугольника
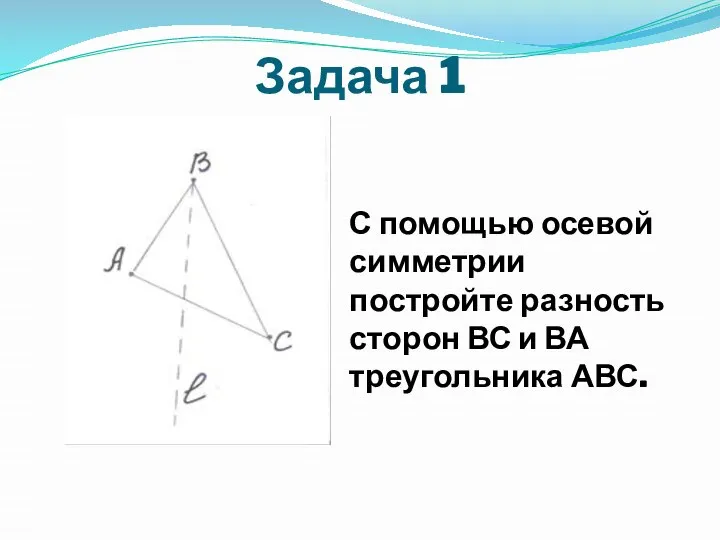
АВС.
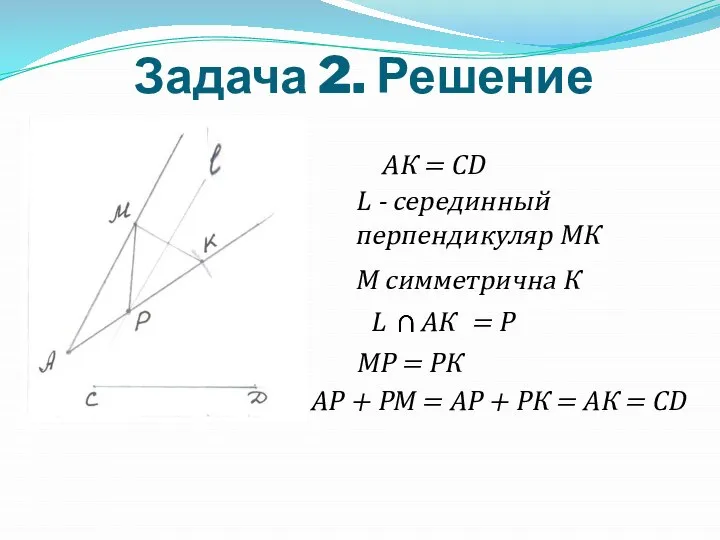
Слайд 8Задача 2
Дан угол с вершиной в точке А и точка М, принадлежащая

одной из его сторон. Найдите на другой стороне этого угла такую точку Р, что сумма расстояний от точки Р до точек М и А равна длине отрезка СD.






 Отбор корней в тригонометрическом уравнении
Отбор корней в тригонометрическом уравнении The most attractive mathematical formulas
The most attractive mathematical formulas Простые задачи на умножение и деление
Простые задачи на умножение и деление Презентация на тему Платоновы тела Правильные выпуклые многогранники 10 класс
Презентация на тему Платоновы тела Правильные выпуклые многогранники 10 класс  Решение задач. Подготовка к контрольной работе
Решение задач. Подготовка к контрольной работе Арифметическая прогрессия в истории
Арифметическая прогрессия в истории Объемы многогранников и тел вращения. Устная работа
Объемы многогранников и тел вращения. Устная работа Презентация на тему Параллельные прямые, треугольники
Презентация на тему Параллельные прямые, треугольники  Назовите числа <4
Назовите числа <4 Арсенал интерактивных методов и приемов для уроков математики
Арсенал интерактивных методов и приемов для уроков математики Математический расчет или интуиция, что надежней?
Математический расчет или интуиция, что надежней? Решение задач. Урок №68
Решение задач. Урок №68 Математическая викторина. 1 тур. Занимательные задачи
Математическая викторина. 1 тур. Занимательные задачи Презентация на тему НАХОЖДЕНИЕ ЧАСТИ ОТ ЦЕЛОГО И ЦЕЛОГО ПО ЕГО ЧАСТИ
Презентация на тему НАХОЖДЕНИЕ ЧАСТИ ОТ ЦЕЛОГО И ЦЕЛОГО ПО ЕГО ЧАСТИ  Графическое решение задач на равномерное движение
Графическое решение задач на равномерное движение Презентация на тему Решение задач с помощью пропорции
Презентация на тему Решение задач с помощью пропорции 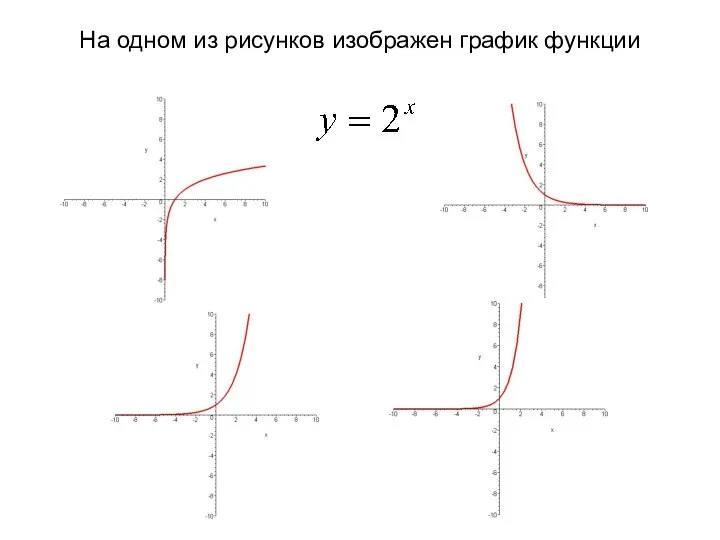 Фронтальный опрос
Фронтальный опрос Соответствия и функции
Соответствия и функции Решение треугольников
Решение треугольников Функції. Графік функції. 7 клас
Функції. Графік функції. 7 клас Линейная регрессия
Линейная регрессия Домашняя самостоятельная работа
Домашняя самостоятельная работа Математика
Математика Практическое применение треугольников в жизни
Практическое применение треугольников в жизни Презентация на тему Решение задач на применение признаков подобия треугольников
Презентация на тему Решение задач на применение признаков подобия треугольников  Приёмы письменного деления на однозначное число
Приёмы письменного деления на однозначное число Страна Математика
Страна Математика Өзіңді – өзің тексер! Мақсаты: оқушылардың білім деңгейын анықтау
Өзіңді – өзің тексер! Мақсаты: оқушылардың білім деңгейын анықтау