Поворот. Пример построения треугольника

Если одна фигура получена из другой фигуры поворотом всех её точек относительно центра О на один и тот же угол в одном и том же направлении, то такое преобразование фигуры называется поворотом.
Поворот

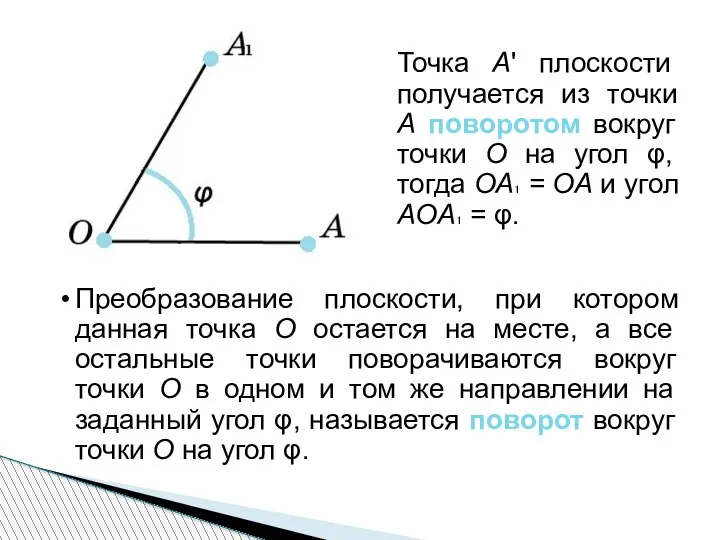
Точка А' плоскости получается из точки А поворотом вокруг точки О на угол φ, тогда OA₁ = OA и угол AOA₁ = φ.
Преобразование плоскости, при котором данная точка О остается на месте, а все остальные точки поворачиваются вокруг точки О в одном и том же направлении на заданный угол φ, называется поворот вокруг точки О на угол φ.

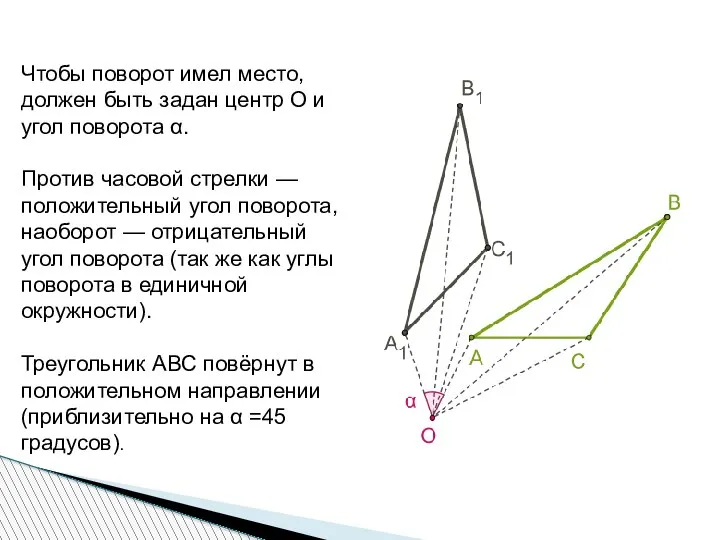
Чтобы поворот имел место, должен быть задан центр О и угол поворота α.
Против часовой стрелки — положительный угол поворота, наоборот — отрицательный угол поворота (так же как углы поворота в единичной окружности).
Треугольник ABC повёрнут в положительном направлении (приблизительно на α =45 градусов).

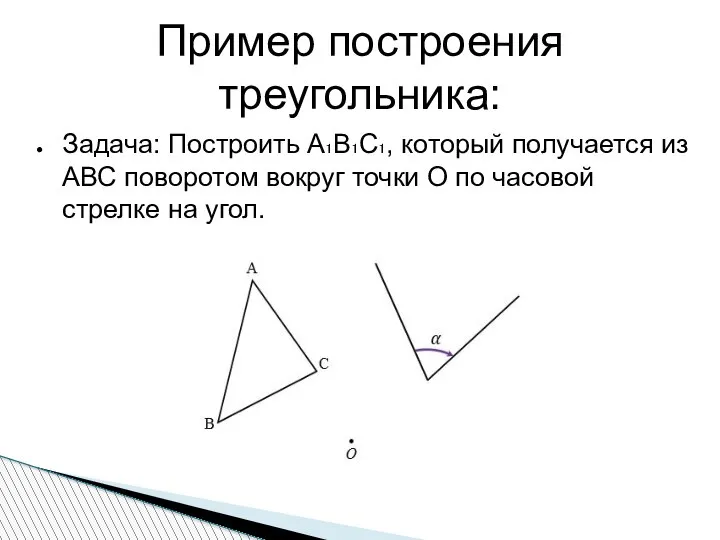
Пример построения треугольника:
Задача: Построить А₁В₁С₁, который получается из АВС поворотом вокруг точки О по часовой стрелке на угол.

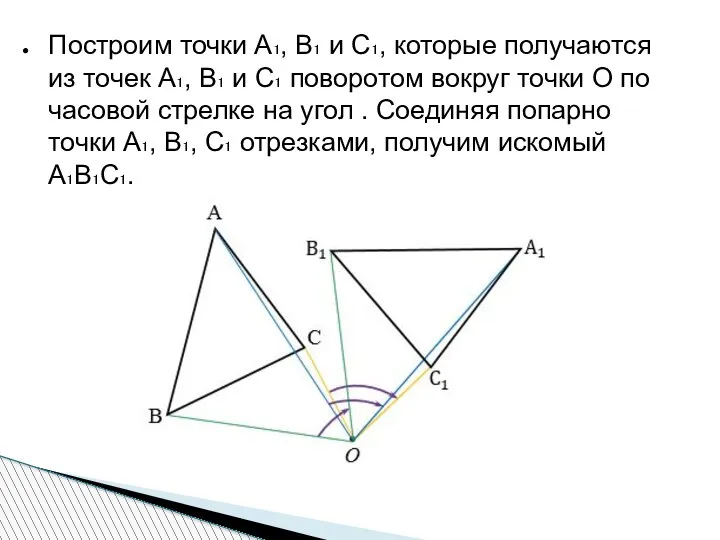
Построим точки А₁, В₁ и С₁, которые получаются из точек А₁, В₁ и С₁ поворотом вокруг точки О по часовой стрелке на угол . Соединяя попарно точки А₁, В₁, С₁ отрезками, получим искомый А₁В₁С₁.

Доказательство того,
что поворот это движение
Дано: О - центр поворота, - угол поворота по часовой стрелке (случай поворота против часовой стрелки рассматривается аналогично), точки E и К отображаются при повороте в точки Е₁ и К₁.
Доказать: поворот - движение.
Доказательство:

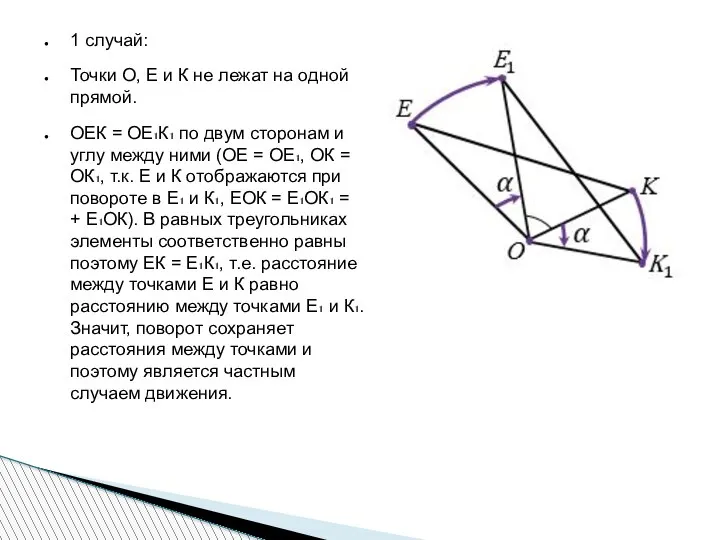
1 случай:
Точки О, E и К не лежат на одной прямой.
ОЕК = ОЕ₁К₁ по двум сторонам и углу между ними (ОЕ = ОЕ₁, ОК = ОК₁, т.к. Е и К отображаются при повороте в Е₁ и К₁, ЕОК = Е₁ОК₁ = + Е₁ОК). В равных треугольниках элементы соответственно равны поэтому ЕК = Е₁К₁, т.е. расстояние между точками Е и К равно расстоянию между точками Е₁ и К₁. Значит, поворот сохраняет расстояния между точками и поэтому является частным случаем движения.

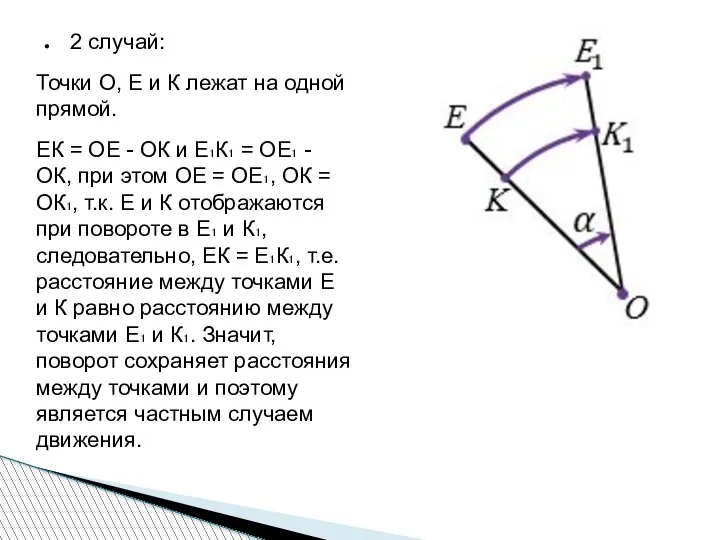
2 случай:
Точки О, Е и К лежат на одной прямой.
ЕК = ОЕ - ОК и Е₁К₁ = ОЕ₁ - ОК, при этом ОЕ = ОЕ₁, ОК = ОК₁, т.к. Е и К отображаются при повороте в Е₁ и К₁, следовательно, ЕК = Е₁К₁, т.е. расстояние между точками Е и К равно расстоянию между точками Е₁ и К₁. Значит, поворот сохраняет расстояния между точками и поэтому является частным случаем движения.

Свойства поворота
Поворот сохраняет расстояния между точками.
Поворот переводит отрезки в отрезки, лучи в лучи и прямые в прямые.

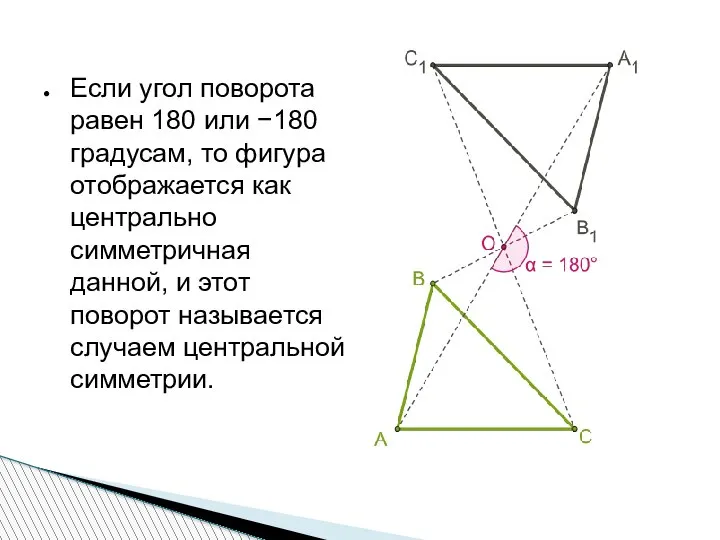
Если угол поворота равен 180 или −180 градусам, то фигура отображается как центрально симметричная данной, и этот поворот называется случаем центральной симметрии.