История системы мер длины (часть 2)

… вначале было три параллельных процес-са:
создание универсальной системы мер длины
изучение секундного маятника
измерение размеров Земли с помощью триангуляций…
Но постепенно они стали сходиться вместе и тогда появился современный «метр»!

Откровения Кардано
Историю создания меры «метр» следует начать с миланского физика и математика Джироламо Кардано (Gerolamo Cardano; 1501…76), который пришел к выводу, что абсолютно точные научные знания о фор-ме и размерах Земли были известны еще до становления цивилизации Древней Эл-лады – в Древнем Египте.
При этом миланец ссылался на авторитет Пифагора, ко-торый якобы утверждал, что древние меры берут начало в Египте, а египтяне, взяв их из природных констант, со-здали Пирамиду Хеопса, чтобы зафиксировать таким об-разом свои знания о размерах нашей планеты.

Теория Фризиуса и…
В 1530 г. Гемма Фризиус (Gemma Frisius; 1508…55) разработал метод триангуляции.
Среди известных учеников Фризиуса был знаменитый в будущем картограф Герард Меркатор, который после окончания уни-верситета работал вместе с Фризиусом над созданием глобусов Земли и Луны.
Но первое применение метода триангуляции на практике состоялось только через 85 лет…

Маятник Галлилея
На рубеже XVI и XVII вв. Галилео Гали-лей (Galileo Galilei; 1564…1642) разрабо-тал общие положения теории математичес-кого маятника.

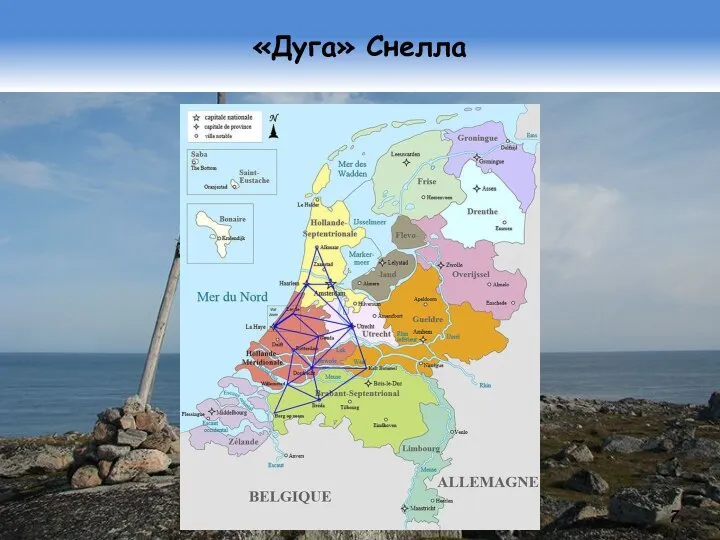
…и практика Снелла
Первые в современной истории градусные измерения выполнил в 1615 г. Виллеброрд Снелл (Снеллиус; Willebrord Snel van Roy-en; 1580…1626). Снелл триангулировал дугу меридиана в 1°11′30″ в Нидерландах между Берген-оп-Зомом и Алкмаром.
Полученная им оценка протяженности одного градуса меридиана была на 3,57% меньше современной. Ошибка Снелла в значительной степени была вызвана недоста-точным качеством и ассортиментом имевшегося у него измерительного оборудования, а также очень короткой базой (всего около 300 м).

«Дуга» Снелла

Волшебная линейка Гривза
Джон Гривз (John Greaves; 1602…52) был среди тех, кто хотел узнать, каковы размеры Земли. В то время в научной среде бытовала уверенность, что (поми-мо египтян) самые достоверные сведе-ния на этот счет имели древние римля-не.
В 1635 г. Гривз отправился в Рим, измерять эталоны древ-неримского фута, pes monetalis. С собой он прихватил уди-вительную линейку: она имела длину в 10 англ. футов и бы-ла выверена по эталону, хранившемуся в Лондонской рату-ше (Guildhall), но разделена она была – вопреки английской метрологической традиции – на 10 000 частей…

Египетские ночи Бураттини
В 1637 г., в возрасте 20 лет, Тито Ливио Бу-раттини (Tito Livio Burattini; 1617…81) (ви-димо под влиянием высказываний Карда-но) поехал в Египет и предпринял несколь-ко попыток обмерить Великую пирамиду.
* Озеро в Фаюмском оазисе, ныне известное как Birket Qarun.
Бураттини, по его словам, измерял «пирамиды, обелис-ки, сфинксы, мумии, руины Александрии, озера Моэ-рис*, египетские, персидские, греческие и римские зда-ния». Ему также приписывают попытку триангуляции территории Египта.

Отеческая забота отца Кирхера
По одной из версий, поездку Бураттини в Египет финансировал о. Афанасий Кирхер (Athanasius Kircher; 1602…80). Кирхер был одним из авторитетнейших ученых своего времени, но его взгляды на жизнь и науку сильно отличались от тех, что стали доми-нировать вскоре после его смерти, поэтому
о. Кирхер на века прослыл безнадежным ретроградом.
Его взаимоотношения с Бураттини освещены скудно и противоречиво, но широко известен тот факт, что не-сколько гравюр последнего были воспроизведены от-цом Кирхером в его знаменитом «Египетском Эдипе» («Oedipus Aegyptiacus», 1652).

Волшебная линейка Гривза (окончание)
В Риме Гривзу не повезло: все показанные ему «этало-ны» не выдерживали никакой критики. И тогда (в 1639 году), памятуя об откровениях Кардано, он отправился в Египет, где встретил… Бураттини!
Итальянец с радостью согласился проделать обмеры Великой пирамиды еще раз (к тому моменту он успел это сделать уже дважды) – с помощью «правильной» линейки Гривза. Правильной она была, во-первых, по-тому, что была сверена с очень авторитетным этало-ном, а во-вторых, её деление полностью соответствова-ло «десятеричным» идеям самого Бураттини.

Египетские ночи Бураттини (окончание)
Вскоре Гривза пригласили преподавать в Оксфорд, и он уехал, оставив свою «чудо-линейку» итальянцу, ко-торый еще пару лет прикладывал её к различным еги-петским древностям.
По возвращении в Европу с Бураттини случилась ка-кая-то «мутная» история: он вроде бы был ограблен и лишился большей части своих египетских записей.
Гривз же все свои данные сберег и позднее издал кни-гу «Piramidographia» (1646), коротая послужила одной из отправных точек для широко известной работы по древней метрологии И. Ньютона.

Секундный маятник Мерсенна
В 1644 г. Марен Мерсенн (Marin Mersenne; 1588…1648) впервые определил длину се-кундного маятника (сегодня это 0,994 м при g = 9,80665 м/с2).
А в 1660 г. Лондонское королевское об-щество (академия наук) предложило ис-пользовать длину секундного маятника в качестве универсальной стандартной еди-ницы длины.
Всё бы хорошо, но…

Пчелиная метрология Тевено
Представление о том, что Международ-ный научный стандарт меры длины дол-жен иметь как объективную, так и исто-рическую основу, настолько укоренилось в умах ученых Нового времени, что в XVII в. серьезное внимание было уделено предложению Мельхиседека Тевено (Mel-chisédech Thévenot; 1620…92), что в ка-
Для обсуждения этой идеи Тевено организовал собрание ученых, которое позднее (в 1666 г.) преобразовалось во французскую Академию наук
честве стандарта линейной меры должен быть принят размер шестиугольных пчелиных сот.

Пчелиная метрология Тевено (окончание)
Странная идея, выбрать в качестве метрологического эталона пчелиные соты, оказалась живучей: в следую-щем столетии её поддерживал Рене де Реомюр (René Antoine de Réaumur; 1683…1757) с добавлением аргу-мента о том, что ульи древних Афин должны были иметь соты тех же размеров, что и современные Рео-мюру французские (!!!).
На чем основывалось это утверждение, неизвестно, но сегодня специалисты выделяют несколько типов сот, размеры которых колеблются в довольно широ-ких пределах.
Так что затея эта явно «не стоила свеч»…

Конфуз Кольбера
При подготовке градусных измерений Пи-кара была выявлена порча эталона фран-цузской меры длины туаза (toise du Châte-let). В 1667 г. новый вариант эталона был утвержден королевским сюринтендантом финансов Кольбером (Jean-Baptiste Col-
bert; 1619…83). Однако вскоре выяснилось, что новый эталон на 0,5% короче старого эталона Гильдии камен-щиков (toise de l'Écritoire). Но Кольбер не захотел при-знать своей ошибки, и нововведение осталось в силе.
Судя по всему, новый эталон был разработан при участии всё того же Пикара…

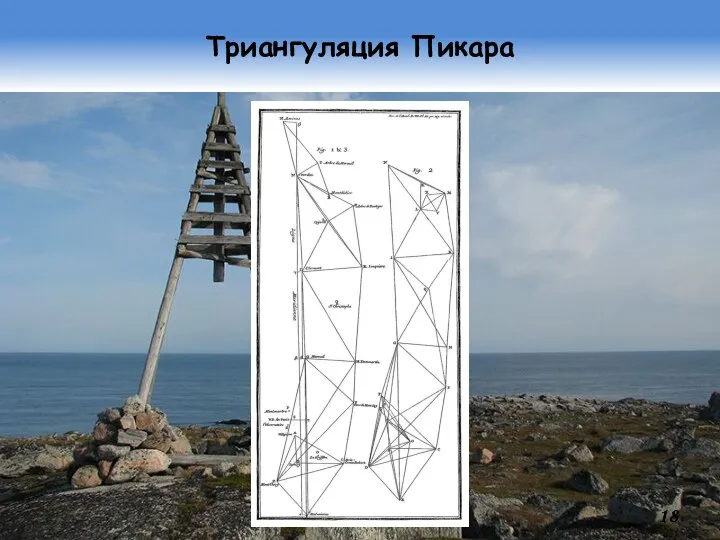
Дуга Пикара
В 1669…70 гг. Жан-Феликс Пикар (Jean-Felix Picard; 1620…82) измерил протяжен-ность дуги меридиана между Парижем и Амьеном (1°04′, 13 треугольников). Изме-рения Пикара были очень точными (по-грешность оценивается в 0,03% и даже в меньшую величину).
По результатам этого измерения в 1674 г. были уточнены протяженности французских путевых мер, сухопутного и морского льё (25 и 20 в градусе меридиана соответ-ственно). Так был создан реальный конкурент маятни-ку…

Триангуляция Пикара

Каверза Рише
В 1670 году Французская академия отправила Жана Рише (Jean Richer; 1630…96) в Запад-ное полушарие для проведения уточняющих астрономических наблюдений. В 1671 г., бу-
дучи в Кайенне (Cayenne; 4°56′ с. ш. 52°20′ з. д.), Рише обнаружил отставание секундного маятника – его при-шлось укорачивать (на 0,3%).
Но этот маятник начал спешить по возвращении во Францию!
Мнения академиков разделились: одни обвиняли Рише в неаккуратности, но другие задумались…

Metro cattolico Бураттини
В 1675 г. в трактате «Misura Universale» Бураттини – вслед за Королевским общест-вом – предложил принять для всей Европы новый метрологический базис, секундный маятник.
Эту меру Бураттини назвал «метр» (metro cattolico, то есть «универсальная мера»).
На его основе итальянец хотел создать со-вершенно новую метрологическую систе-му, в которой «соседние» меры длины со-относились бы друг с другом в пропорции «десять к одному».

Metro cattolico Бураттини (окончание)
Бураттини оценил длину metro cattolico в 4 пальмы Ге-нуи* (996,38 мм), что несколько больше традиционной оценки размера секундного маятника, но metro cattolico всё равно немного не дотягивал до размера современ-ного метра…
Похоже, что Бураттини ещё не знал о «своенравии» ма-ятника…
* 249,095 мм, по оценке Петрушевского.
Следует отметить, что английские ученые никогда не занимались привязкой своих мер к размерам Земли. Это дало повод Вольтеру съязвить однажды про теорию Полюсного сжатия Ньютона…

Бураттини не был первым, кто предложил принять десятичную метрологическую систему, не он изобрёл и секундный маятник,
но он был первым, кто свёл их вместе, и первым, кто привлек к такому проекту внимание широкой публики,
и именно он первым предложил имя «метр» для базовой единицы длины такой системы.

«Дыня» Ньютона и «дыня» Гюйгенса
В 1687 г. Исаак Ньютон (sir Isaac Newton; 1642…1727) высказал (и обосновал!) гипо-тезу о Полюсном сжатии: полюсный ра-диус планеты получился у него на 1/230 ко-роче экваториального. Ньютон считал, что таким образом объясняется эффект замед-ления секундного маятника, обнаружен-ный Рише. Того же мнения придерживался и Гюйгенс (Christiaan Huygens; 1629…95), но у него сжатие получилось меньшим: 1/576 (1690 г.).
Современная оценка Полюсного сжатия составляет 1/298, 257...

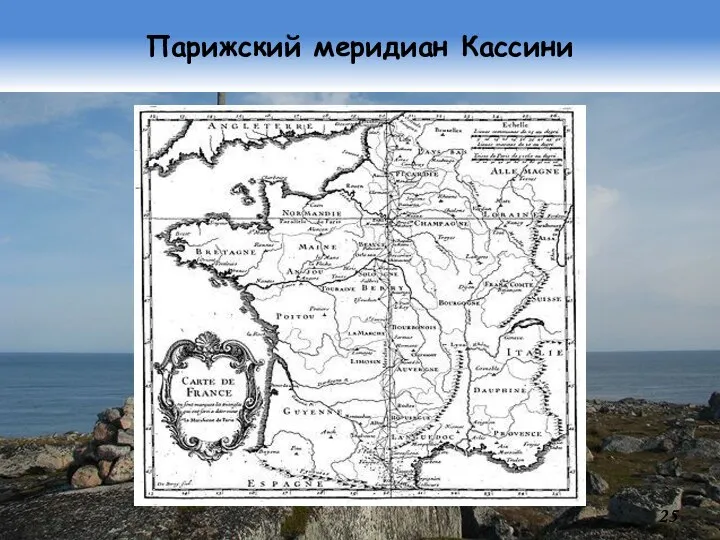
«Яйцо» Кассини
Джованни Доменико Кассини (ит. Giovan-ni Domenico Cassini; фр. Jean-Dominique Cassini; 1625…1712) продолжил работу Пикара: триангуляцию Пикара предстояло продлить до Дюнкерка на севере и до по-бережья Средиземного моря на юге (8°32′, 54 мерных треугольника).
Джованни Кассини не сумел завершить начатое – это сделал его сын Жак (Jacques Cassini; 1677…1756). Градусные измере-ния проходили с большими перерывами и были завершены только в 1718 г. Они дали очень странный результат…

Парижский меридиан Кассини

«Яйцо» Кассини (продолжение)
Из данных Кассини следовало, что Земля вытянута к по-люсам! Это противоречило теории Ньютона, но Касси-ни-младший не хотел признавать даже возможности ошибки в их с отцом работе!
Идея о Полюсном растяжении была настолько спорной, что Французская академия предприняла новые исследо-вания в этом направлении.
Под влиянием разгоревшегося скандала была переоце-нена и работа Пикара: Кассини заявил, что Пикар поль-зовался бракованным туазом («ошибка Пикара», «d'erre-ur de Piard»)…

Toise du Pérou
Чтобы выйти из скандала с измерениями Кассини, Ака-демия решила сделать три вещи:
Создать «не вызывающий сомнений» эталон ме-ры длины.
С помощью этого эталона произвести ревизию измерений Пикара и Кассини
С помощью этого эталона провести макси-мально широкие по охвату градусные измере-ния.

Toise du Pérou (продолжение)
Новый эталон французского «королевского» фута (pied-de-roi) в 1732 г. поручили изгото-вить граверу Ланглуа (Claude Langlois), кото-рому с тех пор было дано монопольное право
производить измерительные линейки для научных ра-бот во всей Франции.
Ланглуа выбрал эталон таким, чтобы в кубе с длиной ребра в 1 pied-de-roi, содержалось 70 парижских ливров воды. Новый эталон был длиннее того, каким пользо-вался Пикар, примерно на 0,114%.

На основе этого фута был изготовлен и новый эталон туаза (в 6 футов) – его предстояло использовать в новой серии градусных измерений…

Toise du Pérou (окончание)
Получив новый эталон тауза, Академия сформировала 2 экспедиции: одну – на экватор, в Перу (теперь это территория Эквадора), вторую – поближе к Полюсу, в Лапландию. Измерения в Перу (в 1735…42 гг.; дуга в 350 км) и в Лапландии (в 1736 г.; дуга 100 км) убеди-тельно доказали, что Земля имеет Полюсное сжатие.
Мера, использованная в Перу («toise du Pérou») позд-нее стала эталоном французской «сажени» (так как ме-ра, использованная в Лапландии, «toise du Laponie», была повреждена).
Жак Кассини был посрамлён!
… но он так и не сдался…

Позор Кассини
В 1739 г. сын Жака Кассини, Цезарь Франсуа Кассини де Тюри (César-François Cassini de Thury; 1714…84), обратился к молодому, но уже авторитетному астроно-му и математику Лакайлю (Nicolas-Louis De la Caille; 1713…62) с предложением повторить измерения, выполненные его дедом и отцом. После двухлетних усилий Кассини де Тюри и Лакайль скорректиро-вали прежние расчеты старших Кассини и Пикара с учетом нового эталона. В изме-рениях старших Кассини было выявлено много мелких ошибок.

Торжество Пикара
К середине XX в. учёные всё же пришли к выводу, что работа Пикара была очень точной.
Если предположить, что Кассини приняли оценку протя-женности «Дуги Пикара» без корректировок, то ошибку надо искать в измерениях дуги между Амьеном и Дюн-керком: примененный там туаз должен был отличаться от эталонного toise du Châtelet образца 1667 г. на 0,37%, что дает его размер 1 956,26 мм. Отсюда размер «коро-левского» фута должен был бы быть 326,04 мм.
В Дюнкерке Кассини использовали старый туаз?

Ошибка Лакайля
Но и Лакайль ухитрился внести определенную сумяти-цу в представления о геометрии Земли: в 1750…54 гг., во время своей астрономической экспедиции в Южную Африку, он выполнил триангуляцию, которая показала, что в Южном полушарии Земля была более плоской, чем в Северном.
Это была ошибка!..
… которую удалось окончательно устранить только в 1838 г.

Инициатива Талейрана
Бурное развитие событий в этой сфере спровоцировала Великая Французская ре-волюция: будущий всесильный дипломат Талейран (Charles Maurice de Talleyrand-Périgord; 1754…1838) – видимо, основы-ваясь на идеях все того же Бураттини, – предложил в качестве эталона новой ме-ры, «метра», использовать длину «се-кундного маятника».
8 мая 1790 г. эта идея была одобрена Национальным собранием Франции, хотя к тому времени уже было из-вестно, что параметры маятника недостаточно стабиль-ны, а данные о плотности Земли отсутствовали…

Инициатива де Борда
В 1791 г. инженер и математик Жан-Шарль де Борда (Jean-Charles, chevalier de Borda; 1733…1799) предложил поделить окружность на 400 «градов»: по 100 в каждой четверти.
Кроме того, де Борда существенно улуч-
шил угломерный лимб, и ему не терпелось применить свое изобретение на практике…
Под давлением де Борда 30 марта 1791 г. Французское Национальное собрание утвердило новую концепцию эталона «метра»: теперь на 1 град земного меридиана должно было идти ровно 100 000 метров (40 000 000 м на весь меридиан).

Злоключения Деламбра и Мешена
Перемерять по этому случаю меридиан (от Дюнкерка до Барселоны) отправили акаде-миков Деламбра (Jean-Baptiste Joseph Delam-bre; 1749…1822) и Мешена (Pierre François André Méchain; 1744…1804). Но работа у них сразу не заладилась: Мишена арестова-ли в Испании.
В результате 1 августа 1793 г. Конвент при-нял «временный» эталон метра на основе данных Кассини де Тюри и Лакайля, а рабо-ты Деламбра и Мишена были приостанов-лены до 7 апреля 1795 г.

В итоге Деламбр и Мишен за «чистых» два года (1795…97) перемерили цепочку из 54 старых мерных треугольников через всю Францию, включая Париж, а также продлили её (61 новый треугольник) через Пиренеи в Испанию (до Барселоны).
Эта триангуляция дала размер метра, незначительно, но отличающийся от уже утвержденного «эталона» (3 парижских фута и 11,296 линии против 3 футов и 11,44 линии, которые были получены из данных Кассини и Лакайля).
Корректировка размера метра была узаконена 10 декабря 1799 г.

Злоключения метра
Для продвижения новой системы мер в сентябре 1798 года был созван Международный конгресс (прибыли только представители союзных Франции стран). Он за-вершил свою работу 25 мая 1799 г.
… однако осенью 1799 г. к власти пришел Наполеон, а ему новая система мер не нравилась…
Не нравилась она и большинству французов…
Потом Франции вообще стало не до «метра»…
Потом не стало самой Наполеоновской Франции…
В итоге метр окончательно утвердился у себя на роди-не только в 1840 г. (закон от 4 августа 1837 г.).
Но тут в дело вмешался Бессель…

Каверза Бесселя
Известный немецкий математик и астро-ном Ф.В. Бессель (Friedrich Wilhelm Bes-sel; 1784…1846) занимался разработкой первой в истории современной науки ма-тематической модели Земного эллипсои-да. В процессе этой работы, в 1841 г., он обнаружил ошибку в вычислениях Делам-бра и Мишена. Скандал!!!
Измерения Пикара, а также Кассини де Тюри и Лакайля оказались более точными, чем «технически совершенное» измерение конца XVIII в.!

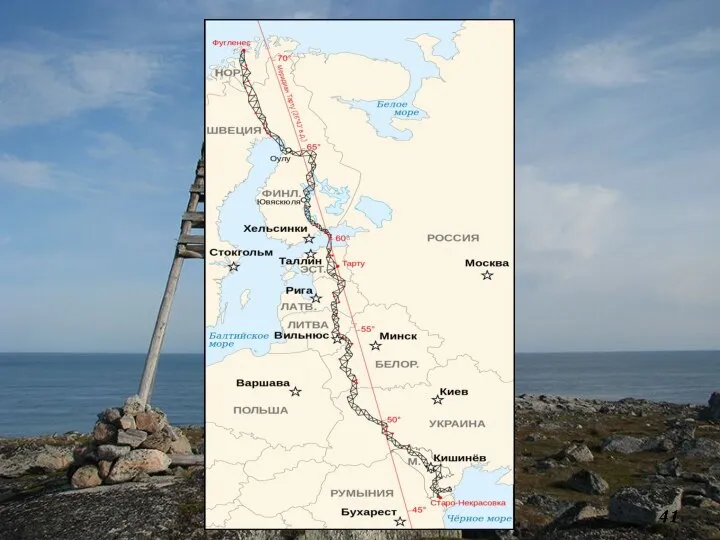
Дуга Струве («Русский след-1»)
«Геодезическая дуга Струве» долгое время была самой масштабной триангуляцией в ми-ре: ее прокладывали с 1816 по 1855 гг. (в те-чение 40 лет!!!) на протяжении 2 820 км (25°20′08″), от побережья Северного Ледови-того океана (мыс Фугленес, недалеко от мыса Норд-Кап в Норвегии (70°40′11″ с.ш.)), и до устья Дуная (с. Старая Некрасовка в Одес-ской области Украины (45°20′03″ с.ш.)) под руководством Фридриха Георга Вильгельма (Василия Яковлевича) Струве (1793…1864) и Карла Ивановича Теннера (1783…1860).
Суммарная ошибка этой триангуляции составила смешные… 50 м!

От Фугленеса до Старой Некрасовки
С 2005 г. Геодезическая дуга Струве объявлена Памятником Всемирного наследия ЮНЕСКО

«Русский след-2»
Оказалось, что «эталон метра, хранящийся в архивах Франции, не составляет [точно одной] десятимиллион-ной части четверти меридиана». Более того, «архивный метр не совпал ни с одним из измерений четверти ме-ридиана [выполненных в период между 1799 и 1869 го-дами] <…> Следовательно, эталон о котором идет речь, должен был утратить характер естественной ме-ры, который ему приписывался при его изготовлении, и в настоящее время он является просто произвольной и условной мерой [выделено нами; Б.В.]» (Из доклада Российской Императорской академии наук, 1869 г.)

«Русский след-3»
Однако данный доклад имел целью не «утопить» метр, а, наоборот, отвести от него избыточные претензии, ко-торые тормозили международную легитимизацию Метрической системы.
Ранее интерес к метру проявляли Н.И. Лобачевский, Ф.И. Петрушевский и А.Я. Купфер, а О.В. Струве, Б.С. Якоби и Д.И. Менделеев активно участвовали в интер-национализации Метрической системы.
В 1870 г. в Париже собралась Международная метри-ческая комиссия (La Commission internationale du mèt-re), в основу работы которой были положены конструк-тивные предложения, высказанные в Докладе РИАН в 1869 г.

Победа метра
Разразившаяся Франко-прусская война прервала рабо-ту Метрической комиссии на 2 года.
Итогом её работы стала дипломатическая конферен-ция, на которой 20 мая 1875 г. Представители 17 госу-дарств подписали Метрическую конвенцию.
Изготовление эталонов метра и килограмма заверши-лось к 1889 г., когда на I Международной конференции мер и весов эти эталоны были распределены между странами по жребию. Россия получила эталоны метра №28 (сегодня признаётся основным) и №11, а кило-грамма – №12 (основной) и №26.
(В США метрическую систему так и не ввели до сих пор, а в Англии – только в 1995 г.)

Судьба метра в России
04.06.1899 в Российской империи принято «Положение о мерах и весах» (закон), раз-работанное Дмитрием Ивановичем Менде-леевым (1834…1907). Оно разрешало при-менение в торговых и иных операциях наравне с российскими мерами, также и (по соглашению сторон) мер Метрической системы.
30.04.1917 принят декрет Временного правительства об обязательном применении Метрической системы на территории России. По понятным причинам, этот закон в жизнь воплощен не был…

Судьба метра в России (окончание)
Советская власть принималась за метр дважды: Декрет СНК РСФСР от 11.09.1918 инициировал переход стра-ны на Метрическую систему, а Декрет СНК РСФСР от 29.05.1922 актуализировал сроки этого перехода.
С 1 октября 1924 г. прекратилось изготовление мерно-го инвентаря старой русской системы мер.
С 1 января 1925 г. Метрическую систему начали вво-дить в Советских учреждениях.
С 1 января 1927 г. Метрическая система стала обяза-тельной в СССР.

Референц-эллипсоид Красовского
(«Русский след-4»)
Самая масштабная триангуляция в мире была осуществлена в СССР под руковод-ством Феодосия Николаевича Красовско-го (1878…1948): Государственной геоде-зической сетью триангуляции, была охвачена половина территории СССР, де-тализация сети сначала соответствовала масштабу 1 : 10 000, а затем была увели-чена до 1 : 2 000. По данным этой сети Александром Александровичем Изото-вым (1907…88) в 1940 г. была разрабо-тана математическая модель поверхности Земли Референц-эллипсоид Красовского.

Прощай, триангуляция!
Модель Красовского и Изотова стала последней, полученной классическим наземным методом: в дальнейшем масштабные геодезические исследования стали осуществляться с помощью космических аппаратов.
И эти исследования, в частности, показали, что Референц-эллипсоид Крассовского оказался предельно точным: погрешность оценки его большой полуоси составила всего 1,7 * 10-5, а оценка сжатия полностью совпала с реальностью.