Содержание
- 2. Что называют системой уравнений? Рассмотрим два линейных уравнения: Y=-x+3 и Y=2x-3 Найдём такую пару значений (x;y),
- 3. Решить систему уравнений - это найти их общие решения Поиск общего решения нескольких уравнений называют решением
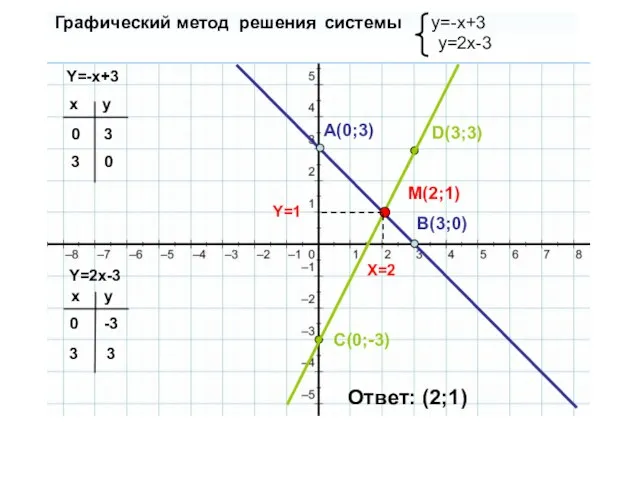
- 4. Графический метод решения системы y=-x+3 y=2x-3 Y=-x+3 Y=2x-3 x y 0 3 x y 0 3
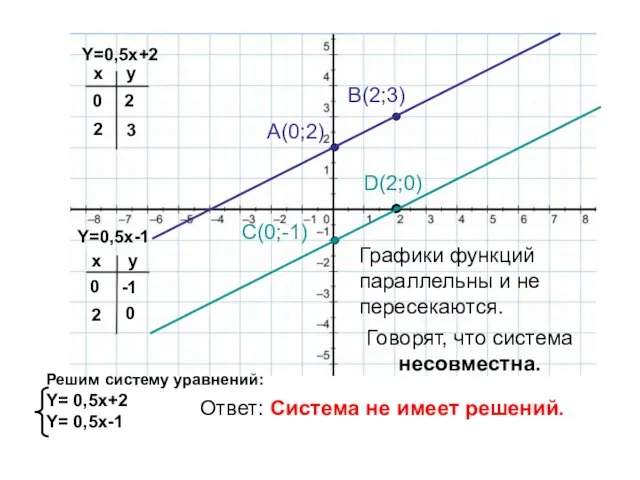
- 5. Y=0,5x-1 Y=0,5x+2 x x y y 0 2 2 3 0 -1 2 0 A(0;2) B(2;3)
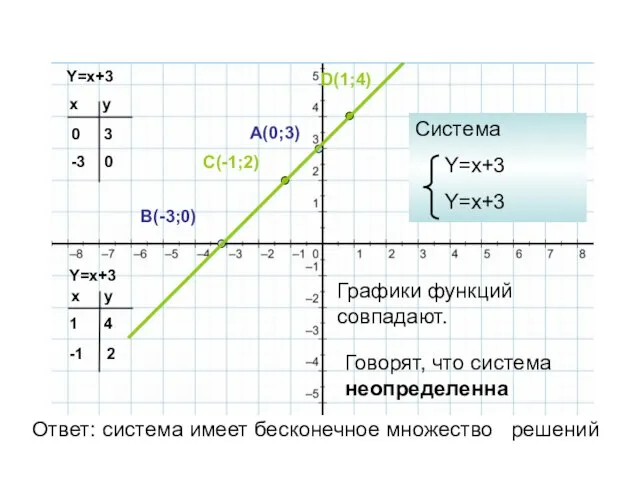
- 6. Y=x+3 Y=x+3 x y 0 -3 x y 1 -1 3 0 4 2 A(0;3) B(-3;0)
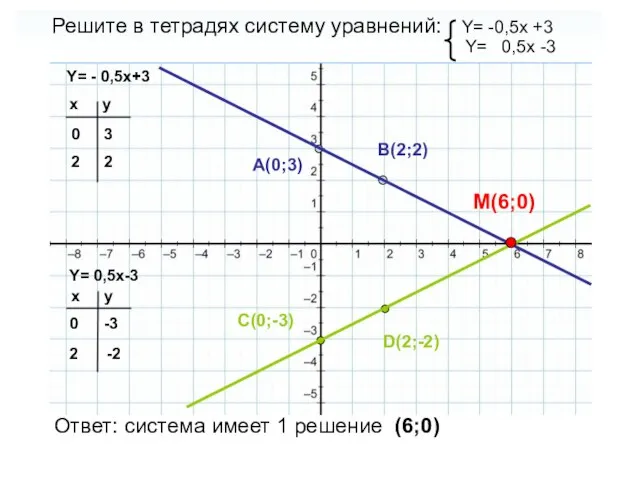
- 7. Решите в тетрадях систему уравнений: Y= -0,5x +3 Y= 0,5x -3 Y= - 0,5x+3 Y= 0,5x-3
- 9. Скачать презентацию


 Решение уравнений. 6 класс
Решение уравнений. 6 класс Теорема Пифагора. Решение задач. Урок для 8 класса
Теорема Пифагора. Решение задач. Урок для 8 класса Тригонометрические функции. Формулы двойного угла
Тригонометрические функции. Формулы двойного угла Графики функций у = ах2+n и y= a(x – m)2
Графики функций у = ах2+n и y= a(x – m)2 Многогранники. Призма
Многогранники. Призма Показательная функция
Показательная функция Графы. Способы задания графов. Степени вершин
Графы. Способы задания графов. Степени вершин Элементы линейной алгебры и геометрии выпуклых множеств
Элементы линейной алгебры и геометрии выпуклых множеств Таблица умножения на 2
Таблица умножения на 2 Правильные многоугольники
Правильные многоугольники Вычитание дробных чисел. 5 класс
Вычитание дробных чисел. 5 класс Презентация на тему Алгебраические уравнения произвольных степеней 10 класс
Презентация на тему Алгебраические уравнения произвольных степеней 10 класс  Периметр восьмиугольника
Периметр восьмиугольника Математичний диктант. Паралелограм
Математичний диктант. Паралелограм Векторное кодирование графической информации
Векторное кодирование графической информации Окружность
Окружность Четырехугольник . Прямоугольник. Квадрат
Четырехугольник . Прямоугольник. Квадрат Параллелепипед
Параллелепипед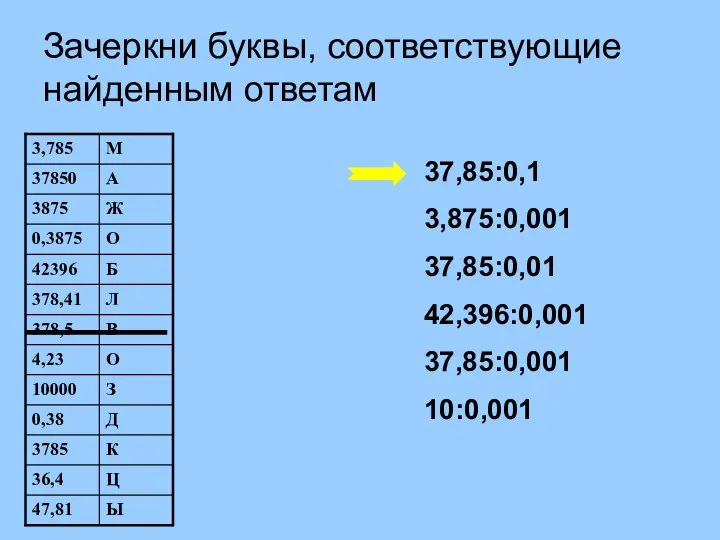 Устная работа (1). Зачеркни буквы, соответствующие найденным ответам
Устная работа (1). Зачеркни буквы, соответствующие найденным ответам Интерактивный тренажёр Реши уравнения
Интерактивный тренажёр Реши уравнения Элементы нелинейного функционального анализа. Гладкие многообразия
Элементы нелинейного функционального анализа. Гладкие многообразия Моделирование – способ, процесс замещения оригинала его аналогом (моделью)
Моделирование – способ, процесс замещения оригинала его аналогом (моделью) Задачи на проценты
Задачи на проценты Живая планета!
Живая планета! Квадратные уравнения
Квадратные уравнения Устный счет в пределах 10. Состав чисел 7, 8
Устный счет в пределах 10. Состав чисел 7, 8 Моделирование на графах
Моделирование на графах Стороны треугольника пропорциональны синусам противолежащих углов
Стороны треугольника пропорциональны синусам противолежащих углов