Презентация на тему Графический способ решения систем уравнений

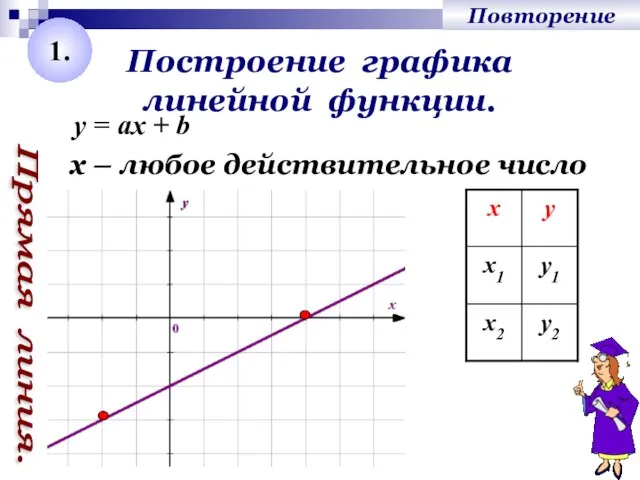
Построение графика
линейной функции.
Прямая линия.
y = ах + b
х – любое действительное число
1.
Повторение

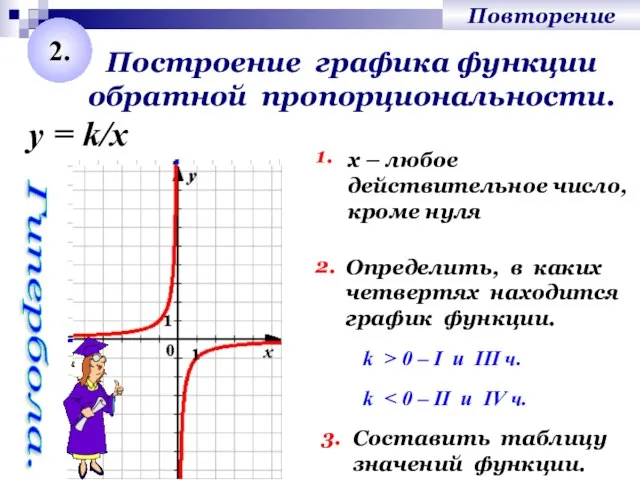
Построение графика функции обратной пропорциональности.
1.
Определить, в каких
четвертях находится
график функции.
2.
Составить таблицу
значений функции.
Гипербола.
у = k/x
k > 0 – I u III ч.
k < 0 – II u IV ч.
3.
х – любое
действительное число,
кроме нуля
2.
Повторение

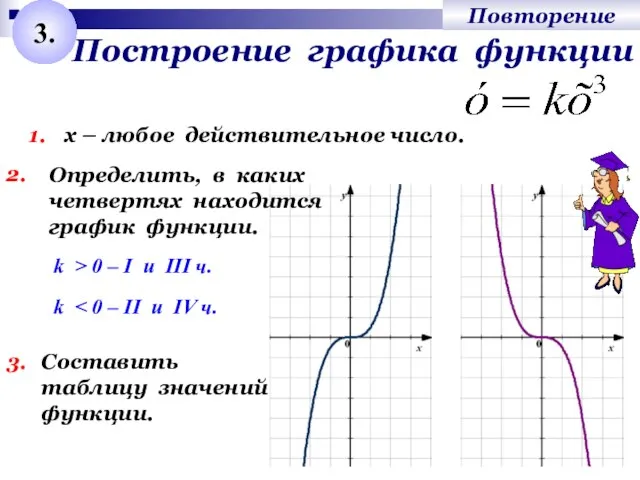
Построение графика функции
3.
1.
х – любое действительное число.
2.
k > 0 – I u III ч.
k < 0 – II u IV ч.
Определить, в каких
четвертях находится
график функции.
Составить
таблицу значений
функции.
3.
Повторение

Повторение
4.
Построение окружности.
r – радиус окружности.
(x0; у0 )– координаты
центра окружности.

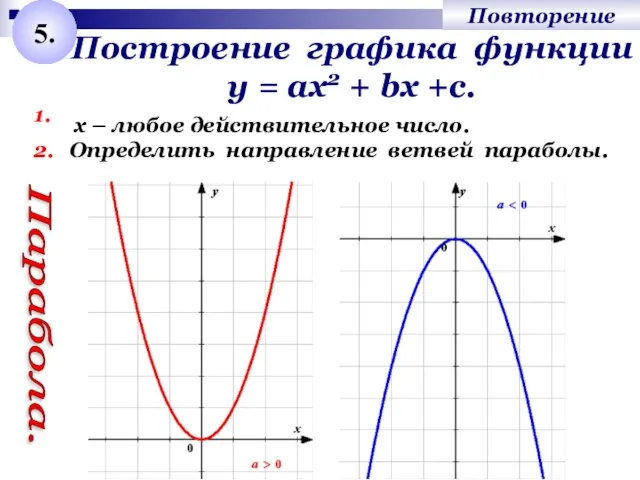
Построение графика функции у = ах2 + bх +с.
1.
Определить направление ветвей параболы.
Парабола.
5.
2.
х – любое действительное число.
Повторение

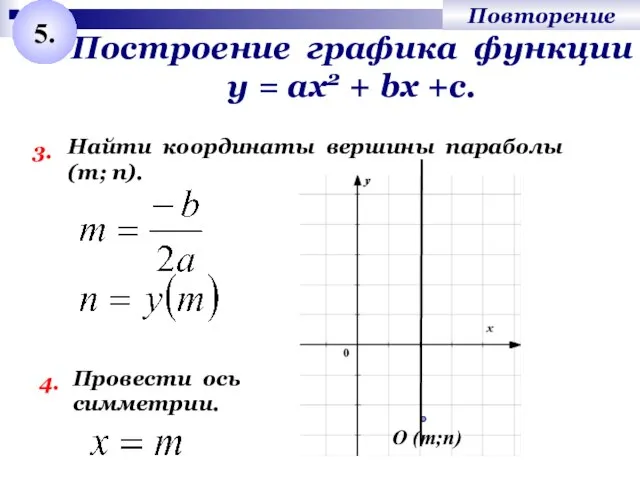
Построение графика функции у = ах2 + bх +с.
3.
Найти координаты вершины параболы
(т; п).
4.
Провести ось
симметрии.
О (т;п)
Повторение
5.

Построение графика функции у = ах2 + bх +с.
5.
Определить точки пересечения графика
функции с осью Ох, т.е. найти нули
функции.
(х1;0)
(х2;0)
Повторение
5.

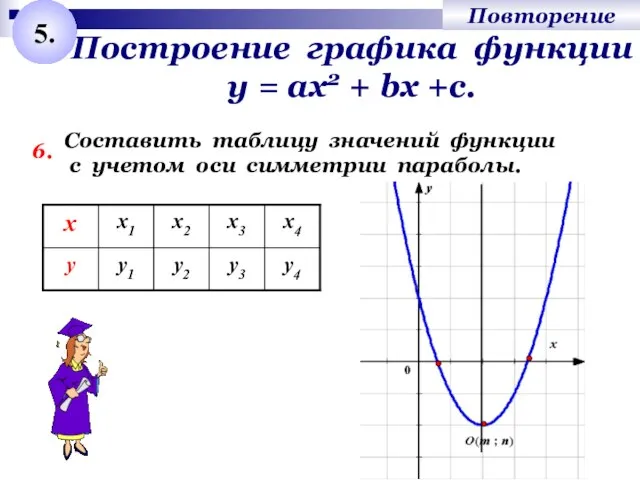
Построение графика функции у = ах2 + bх +с.
6.
Составить таблицу значений функции с учетом оси симметрии параболы.
Повторение
5.

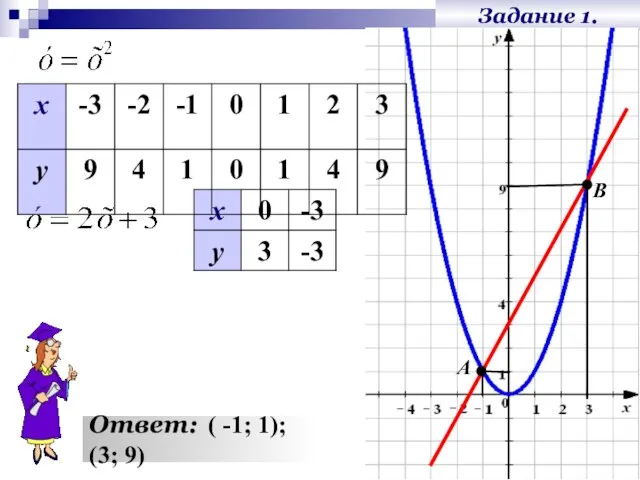
Задание 1.
Решить графически
систему уравнений.
1.
2.
Построим графики
функций в одной
системе координат.
3.
Составим таблицы значений функций.

Задание 1.
Ответ: ( -1; 1); (3; 9)
А
В

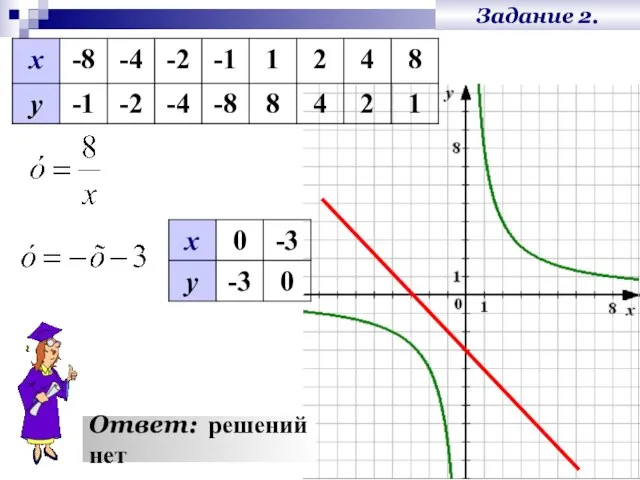
Задание 2.
Решить графически
систему уравнений.
1.
2.
Построим графики
функций в одной
системе координат.
3.
Составим таблицы значений функций.

Задание 2.
Ответ: решений нет

Задание 3.
Решить графически
систему уравнений.
Подробно

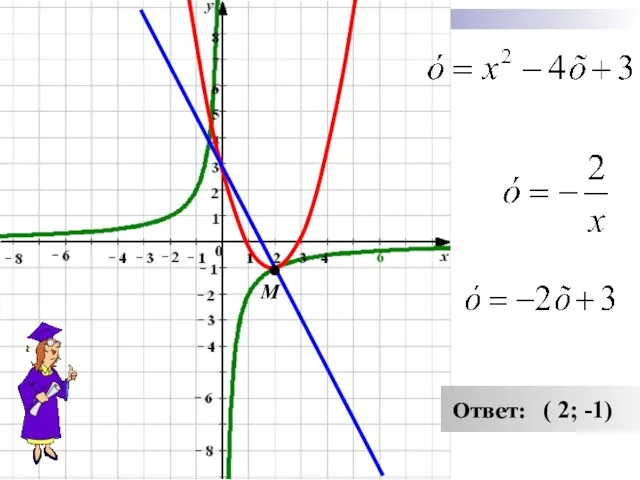
х – любое действительное число.
1.
2.
Графиком функции является парабола, ветви
которой направлены вверх. a > 0
3.
Найдём координаты вершины параболы
4.
Дополнительные точки:
М ( 2; -1)

М
Ответ: ( 2; -1)

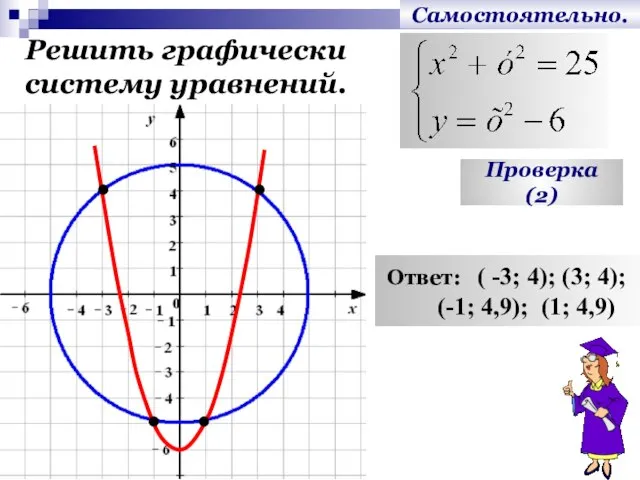
Самостоятельно.
Решить графически
систему уравнений.
Проверка (2)
Ответ: ( -3; 4); (3; 4);
(-1; 4,9); (1; 4,9)

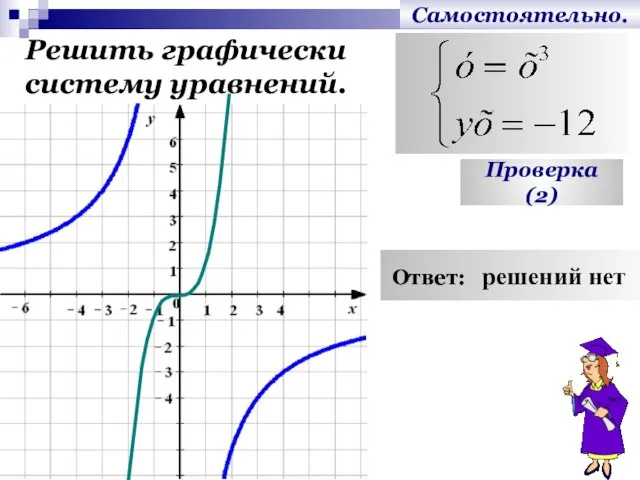
Самостоятельно.
Решить графически
систему уравнений.
Проверка (2)
Ответ: решений нет