Содержание
- 2. Историческая справка Тригонометрические функции возникли впервые в связи с исследованиями в астрономии и геометрии. Соотношения отрезков
- 3. Для тригонометрических функций можно определить обратные функции (круговые функции, аркфункции). Они обозначаются соответственно , , ,
- 4. Почему можно определить обратную тригонометрическую функцию. Теорема о корне: Пусть функция f возрастает (или убывает) на
- 5. Арксинус Арксинус -угол из промежутка синус которого равен а. Если , то Функция y = arcsinx
- 6. Арккосинус Арккосинус -угол из промежутка , косинус которого равен а. Если , то Функция y =
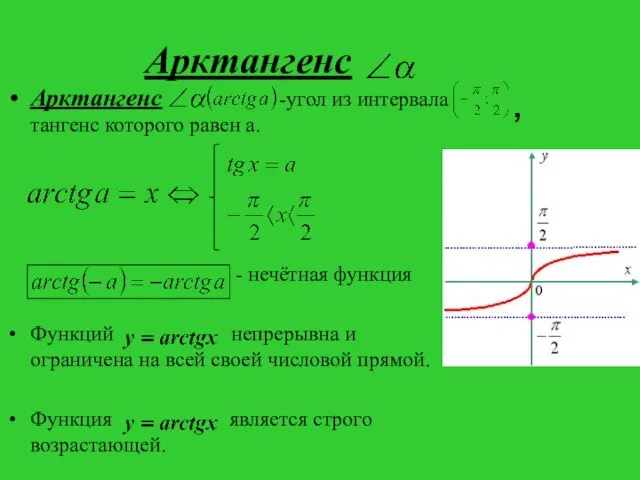
- 7. Арктангенс Арктангенс -угол из интервала тангенс которого равен а. - нечётная функция Функций непрерывна и ограничена
- 8. Арккотангенс Арккотангенс -угол из интервала , котангенс которого равен а. Функция непрерывна и ограничена на всей
- 9. Преобразований сумм обратных тригонометрических функций На промежутке функция возрастает, т.е. каждое свое значение принимает ровно один
- 10. Уравнения и неравенства, левая и правая части которых являются одноименными обратными тригонометрическими функциями Решение уравнений и
- 11. Примеры Пример 1. Решить уравнение Решение. Уравнение равносильно системе: Замечание. Решать неравенство, входящее в систему не
- 12. Пример 2. Решить неравенство 3arcsin 2x Решение.
- 13. II Замечание. Какой из двух равносильных систем пользоваться при решении уравнений 2а), зависит от того, какое
- 14. Пример 3. Решить неравенство Решение. Ответ: {– 2}.
- 15. Пример 4. Решить уравнение Решение. Так как , то имеет место следующая цепочка равносильных преобразований:
- 16. III а) arctg f(x) = arctg g(x) f(x) = g(x); б) acrtg f(x) ≤ arctg g(x)
- 17. Пример 5. Решить неравенство Решение. Неравенство равносильно следующему:
- 18. Уравнения и неравенства, левая и правая части которых являются разноименными обратными тригонометрическими функциями При решении уравнений
- 19. Рассуждая аналогично, можно получить следующие переходы: Замечание. Корнем каждого из уравнений (1)–(4) может быть только такое
- 20. Пример 6. Решить уравнение Решение. Корень является посторонним. Ответ: {1}. Примеры
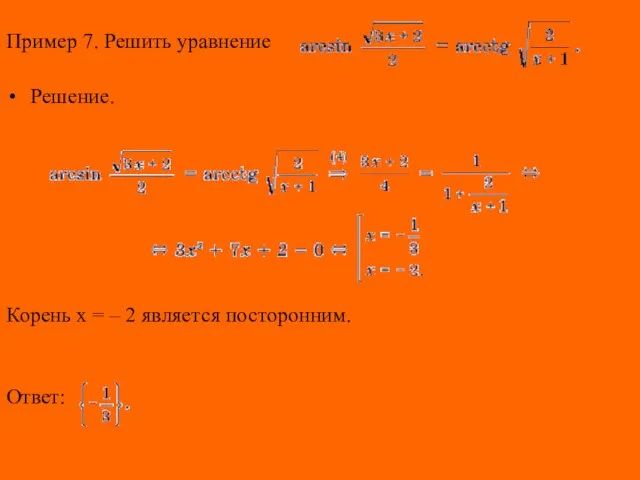
- 21. Пример 7. Решить уравнение Решение. Корень x = – 2 является посторонним. Ответ:
- 22. Пример 8. Решить уравнение arctg (2sin x) = arcctg (cos x). Решение. Корни вида являются посторонними.
- 23. При решении неравенств, левая и правая части которых представляют собой разноименные обратные тригонометрические функции, целесообразно использовать
- 24. 3) Решим неравенство f(x) ≤ 0 методом интервалов. Замечание 4. Заметим, что найдя корень уравнения можно
- 25. При решении уравнений и неравенств данного типа, содержащих параметры, становится актуальным вопрос о равносильности преобразований. Чтобы
- 26. Замена переменной Некоторые уравнения и неравенства, содержащие обратные тригонометрические функции, можно свести к алгебраическим, сделав соответствующую
- 27. Пример 11. Решить неравенство Решение. Пусть arccos x = t, 0 ≤ t ≤ π. Тогда
- 28. Пример 12. Решить уравнение Решение. Данное уравнение равносильно следующему: Пусть arcsin x = t, Тогда
- 29. IV. Использование свойств монотонности и ограниченности обратных тригонометрических функций Решение некоторых уравнений и неравенств, содержащих обратные
- 30. Пример 13. Решить уравнение 2arcsin 2x = 3arccos x. Решение. Функция y = 2arcsin 2x является
- 31. Пример 15. Решить неравенство Решение. Левая часть неравенства представляет собой монотонно убывающую на отрезке функцию Уравнение
- 32. Пример 16. Решить уравнение arcsin (x(x + y)) + arcsin (y(x + y)) = . Решение.
- 33. Уравнения и неравенства с параметрами. Пример 1. Решить уравнение с параметром a: Решение. Уравнение равносильно уравнению
- 34. Пример 2. Решить неравенство с параметром a: Решение. Неравенство равносильно системе Решать последнюю систему можно графо-аналитическим
- 35. Пример 3. Решить уравнение с параметром a: arcctg (x – 2a) = arctg (2x – a).
- 37. Скачать презентацию
































 МВ УРОК 22 ГЕО ТРЕУГОЛЬНИК
МВ УРОК 22 ГЕО ТРЕУГОЛЬНИК Четырехзначные числа
Четырехзначные числа Уравнения с двумя переменными
Уравнения с двумя переменными Решение задач на межпредметные связи
Решение задач на межпредметные связи От перестановки множителей произведение не изменяется
От перестановки множителей произведение не изменяется Презентация на тему Длиннее короче
Презентация на тему Длиннее короче  Графики кусочных функций
Графики кусочных функций Веселый счет (Счет в прямом и обратном порядке в пределах 10)
Веселый счет (Счет в прямом и обратном порядке в пределах 10) Степень и ее свойства
Степень и ее свойства Кругові приклади
Кругові приклади Величины. Свойства величин
Величины. Свойства величин Многонранники в нашей жизни
Многонранники в нашей жизни Куб
Куб Подготовка к ЕГЭ. Повторение. Математика
Подготовка к ЕГЭ. Повторение. Математика Косинус угла
Косинус угла Занимательная геометрия
Занимательная геометрия Сближение меридианов. Международное геомагнитное аналитическое поле IGRF
Сближение меридианов. Международное геомагнитное аналитическое поле IGRF Понятие цилиндра
Понятие цилиндра Измерение площадей. Площадь прямоугольника
Измерение площадей. Площадь прямоугольника Teorema_polnoy_veroyatnosti
Teorema_polnoy_veroyatnosti Приближение десятичных дробей
Приближение десятичных дробей Особенности набора математических формул в Microsoft
Особенности набора математических формул в Microsoft Презентация на тему Решето Эратосфена
Презентация на тему Решето Эратосфена  Обратные тригонометрические функции
Обратные тригонометрические функции tema_2_1_metrologia (1)
tema_2_1_metrologia (1) Числовая последовательность
Числовая последовательность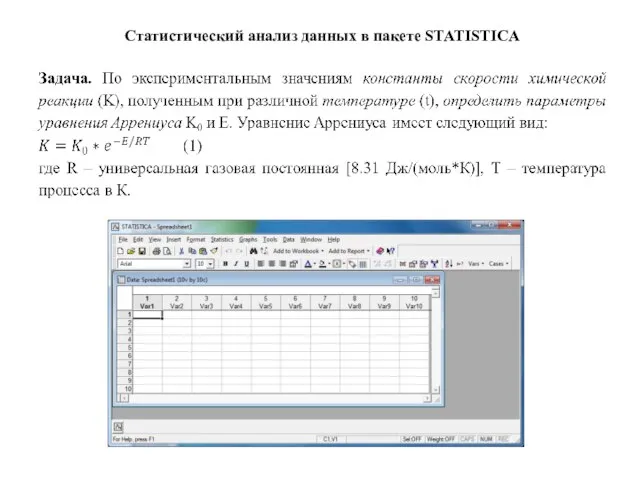 Статистический анализ данных в пакете Statistica
Статистический анализ данных в пакете Statistica Игра
Игра