Внеклассное мероприятие. Путешествие в мир многогранников

содержание
Симметрия
Правильные многогранники
Полуправильные многогранники
Звездчатые тела

Слово "симметрия" ("symmetria") имеет греческое происхождение и означает "соразмерность". В повседневном языке под симметрией понимают чаще всего упорядоченность, гармонию, соразмерность. Гармоничная согласованность частей и целого является главным источником эстетической ценности симметрии.
симметрия

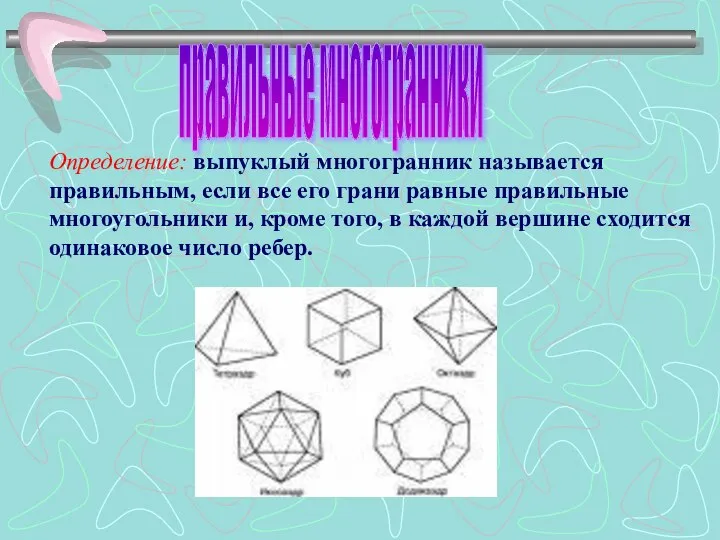
Определение: выпуклый многогранник называется правильным, если все его грани равные правильные многоугольники и, кроме того, в каждой вершине сходится одинаковое число ребер.
правильные многогранники

Учение о правильных многогранниках изложил в своих трудах древнегреческий ученый, философ-идеалист Платон. С тех пор правильные многогранники стали называться платоновыми телами.

С каждым типом многогранника другой древнегреческий философ-естествоиспытатель Аристотель связал пять стихий:
1.Тетраэдр- огонь
2.Октаэдр – воздух
3.Икосаэдр – вода
4.Гексаэдр – Земля
5.Додекаэдр - космос

Тетраэдр составлен из четырех равносторонних треугольников. Каждая его вершина является вершиной трех треугольников. Сумма плоских углов при каждой вершине равна 180 градусов. Таким образом, тетраэдр имеет 4 грани, 4 вершины и 6 ребер.
Тетраэдр

Куб составлен из шести квадратов. Каждая его вершина является вершиной трех квадратов. Сумма плоских углов при каждой вершине равна 270 градусов. Таким образом, куб имеет 6 граней, 8 вершин и 12 ребер.
Гексаэдр (Куб)

Октаэдр составлен из восьми равносторонних треугольников. Каждая его вершина является вершиной четырех треугольников. Сумма плоских углов при каждой вершине равна 240 градусов. Таким образом, октаэдр имеет 8 граней, 6 вершин и 12 ребер.
Октаэдр

Икосаэдр составлен из двадцати равносторонних треугольников. Каждая его вершина является вершиной пяти треугольников. Сумма плоских углов при каждой вершине равна 300 градусов. Таким образом икосаэдр имеет 20 граней, 12 вершин и 30 ребер.
Икосаэдр

Додекаэдр составлен из двенадцати равносторонних пятиугольников. Каждая его вершина является вершиной трех пятиугольников. Сумма плоских углов при каждой вершине равна 324 градусов. Таким образом, додекаэдр имеет 12 граней, 20 вершин и 30 ребер.
Додекаэдр

Определение: Тела, грани которых являются правильными многоугольниками разных типов, но все многогранные углы по-прежнему равны называются полуправильными многогранниками.
антипризмы
полуправильные многогранники