Содержание
- 2. Содержание Определение. Примеры построений сечений. Задания на построение сечений.
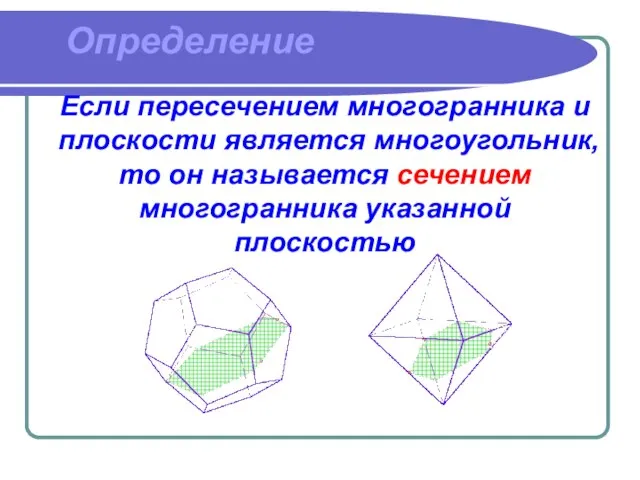
- 3. Определение Если пересечением многогранника и плоскости является многоугольник, то он называется сечением многогранника указанной плоскостью
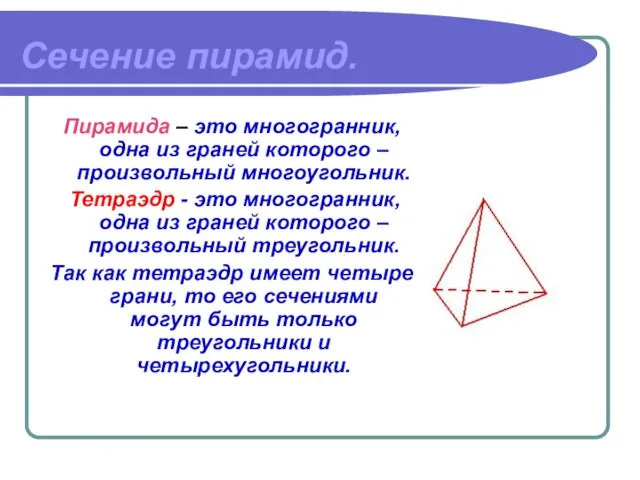
- 4. Сечение пирамид. Пирамида – это многогранник, одна из граней которого – произвольный многоугольник. Тетраэдр - это
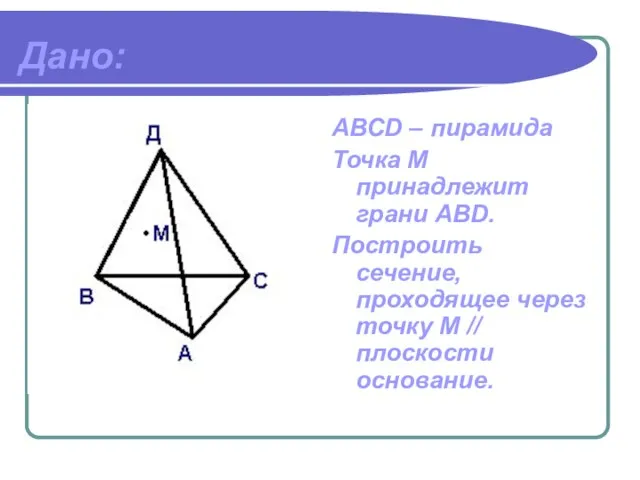
- 5. Дано: АВСD – пирамида Точка М принадлежит грани ABD. Построить сечение, проходящее через точку М //
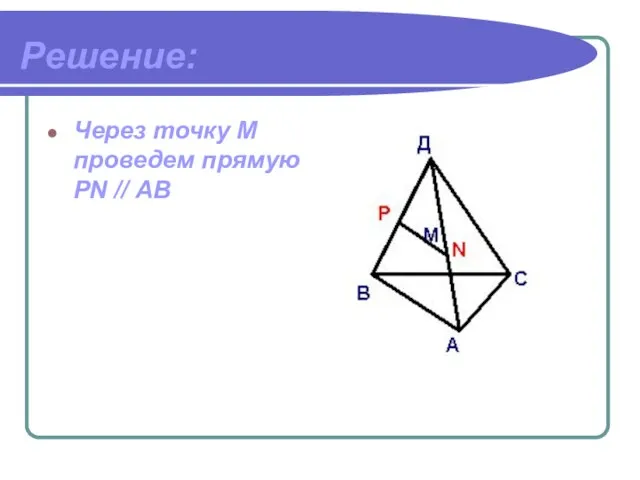
- 6. Решение: Через точку М проведем прямую PN // АВ
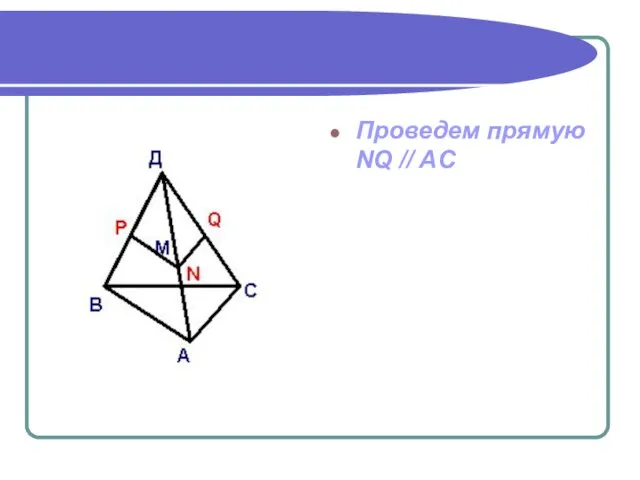
- 7. Проведем прямую NQ // AC
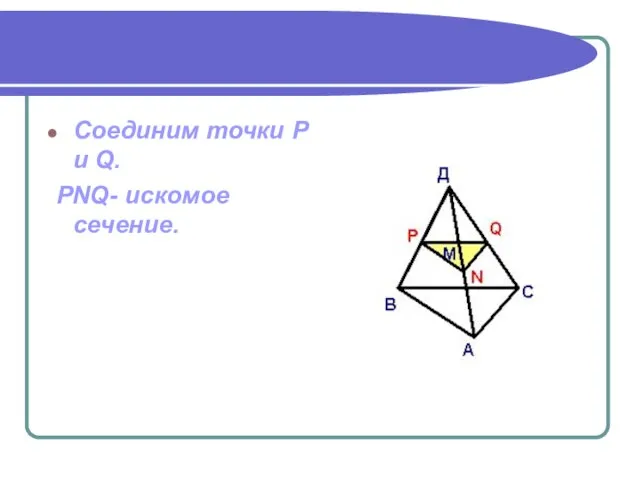
- 8. Соединим точки P и Q. PNQ- искомое сечение.
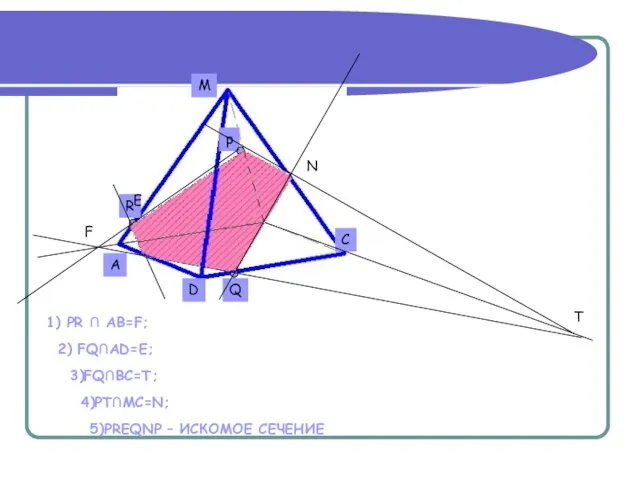
- 9. Дано: Пирамида MABCD. Постройте сечение пирамиды, проходящее через точки P, Q, R. Известно, что точка P
- 10. F T 1) PR ∩ AB=F; 2) FQ∩AD=E; 3)FQ∩BC=T; 4)PT∩MC=N; 5)PREQNP – ИСКОМОЕ СЕЧЕНИЕ Е N
- 11. Сечение куба Прямоугольный параллелепипед, у которого все три измерения равны, называется кубом. Куб имеет 6 граней.
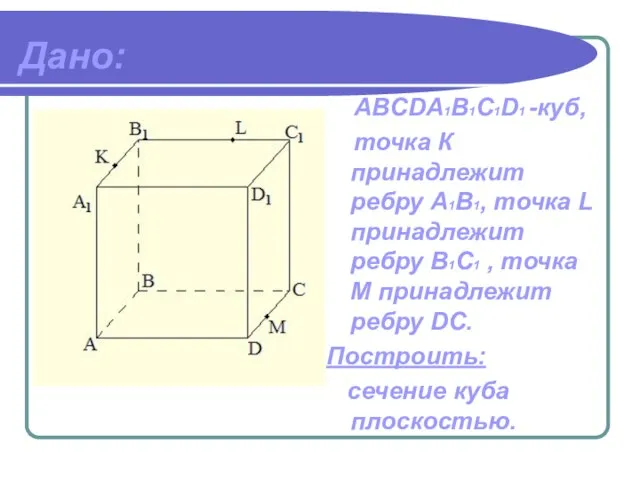
- 12. Дано: ABCDА1B1C1D1 -куб, точка К принадлежит ребру A1В1, точка L принадлежит ребру В1C1 , точка М
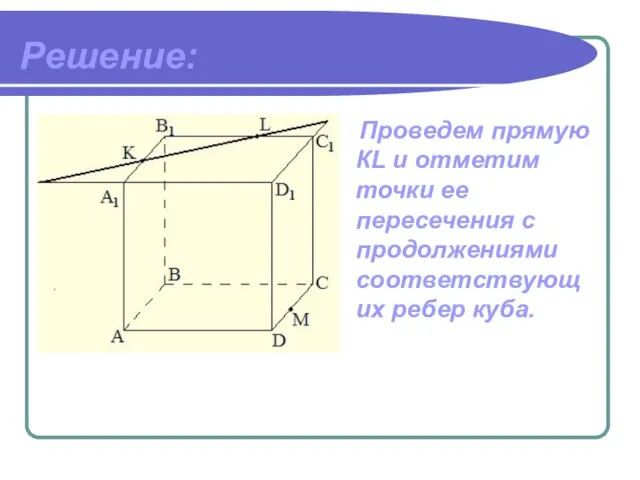
- 13. Решение: Проведем прямую КL и отметим точки ее пересечения с продолжениями соответствующих ребер куба.
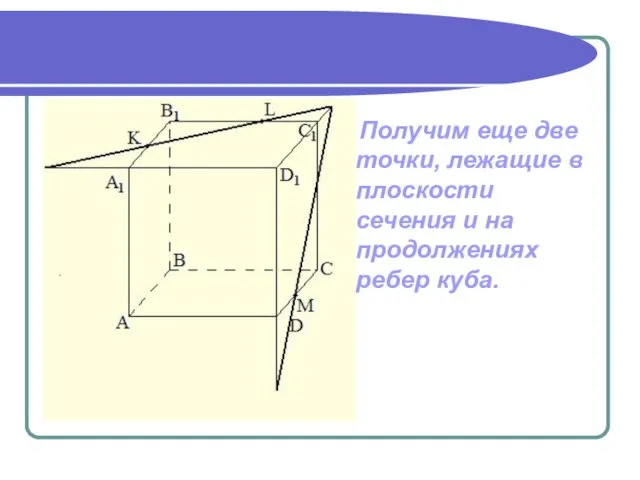
- 14. Получим еще две точки, лежащие в плоскости сечения и на продолжениях ребер куба.
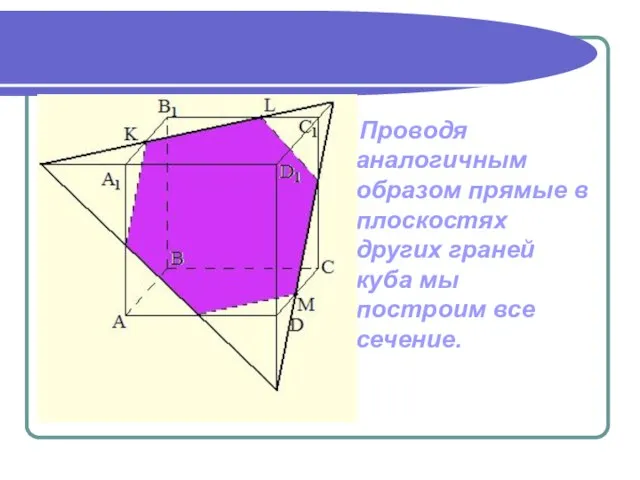
- 15. Проводя аналогичным образом прямые в плоскостях других граней куба мы построим все сечение.
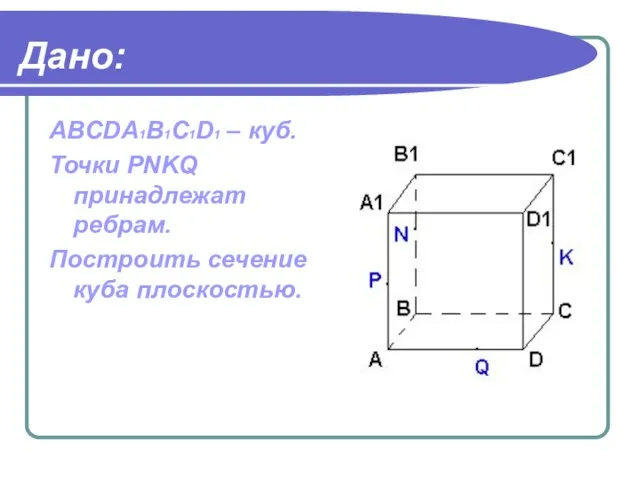
- 16. Дано: ABCDA1B1C1D1 – куб. Точки PNKQ принадлежат ребрам. Построить сечение куба плоскостью.
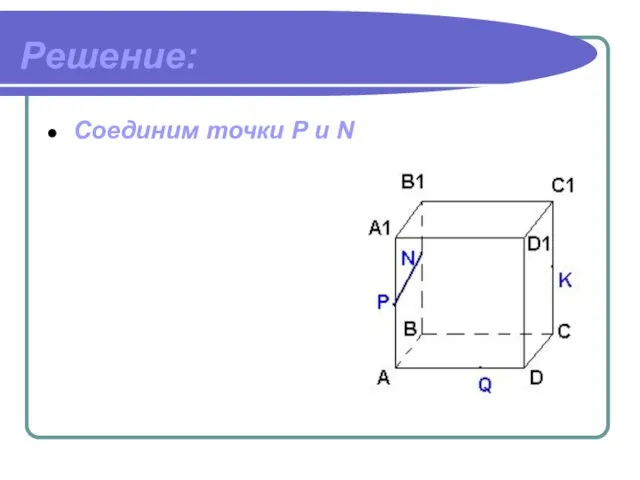
- 17. Решение: Соединим точки P и N
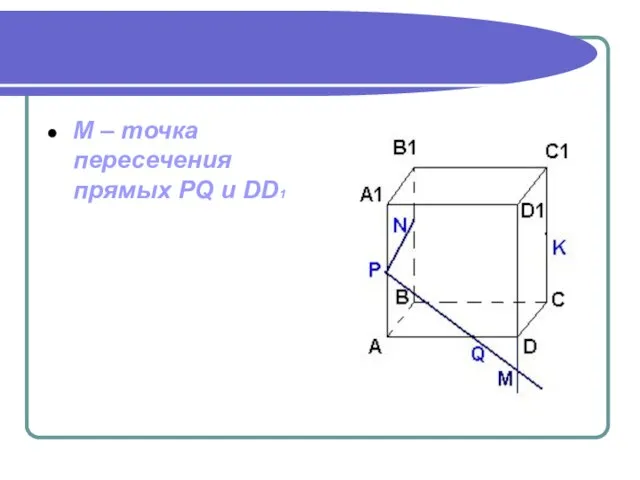
- 18. М – точка пересечения прямых PQ и DD1
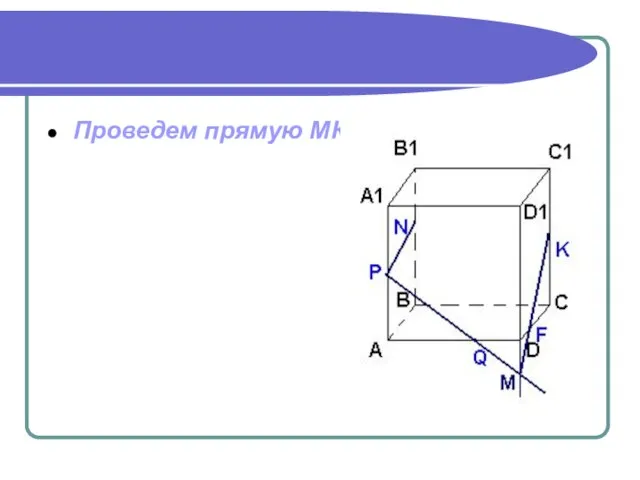
- 19. Проведем прямую МК
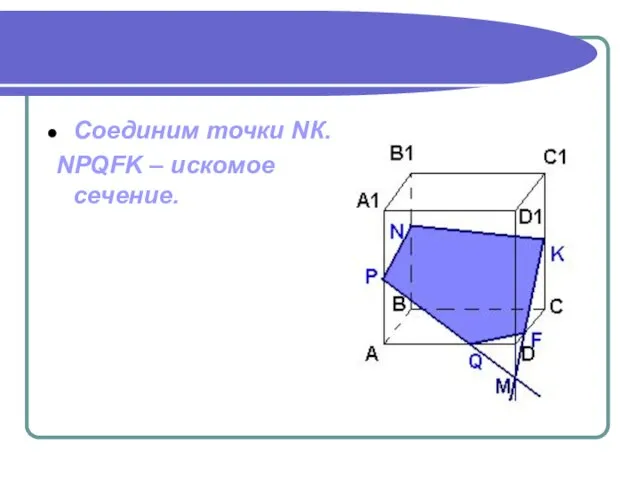
- 20. Соединим точки NК. NPQFK – искомое сечение.
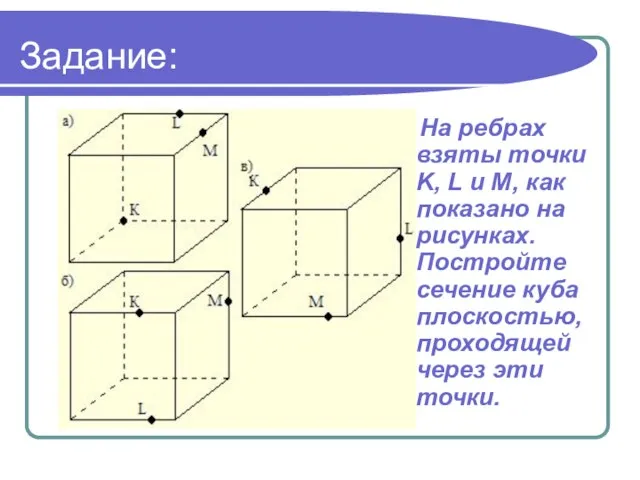
- 21. Задание: На ребрах взяты точки K, L и M, как показано на рисунках. Постройте сечение куба
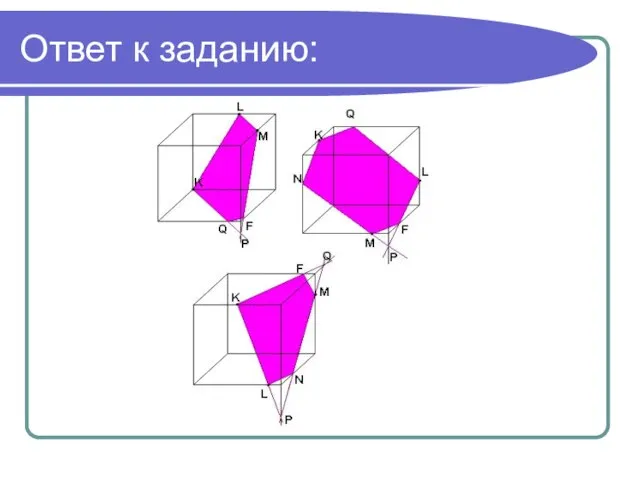
- 22. Ответ к заданию:
- 23. Мир многогранников!
- 24. «Правильных многогранников вызывающе мало, но этот весьма скромный по численности отряд сумел пробраться в самые глубины
- 25. За каждым многогранником закреплено его значение, НАПРИМЕР: Тетраэдр является огнём!
- 26. куб-земля
- 27. октаэдр-воздух
- 28. Даже пчёлы знакомы с понятием многогранник!!!
- 30. Скачать презентацию









 Проект по математике Задачи-расчеты из моей жизни
Проект по математике Задачи-расчеты из моей жизни Устный счёт Живые примеры от Гнома
Устный счёт Живые примеры от Гнома Модель плоскости
Модель плоскости Степень, графики функций, пропорции на уроках математики и физики
Степень, графики функций, пропорции на уроках математики и физики Деление
Деление Векторы
Векторы Графики функций. Задачи с параметрами
Графики функций. Задачи с параметрами Преобразование выражений, содержащих модуль
Преобразование выражений, содержащих модуль Связь между суммой и слагаемыми (1 класс)
Связь между суммой и слагаемыми (1 класс) Проецирование на две плоскости проекций
Проецирование на две плоскости проекций Презентация на тему Деление с остатком
Презентация на тему Деление с остатком  Шагаем по линейке
Шагаем по линейке Векторное и смешанное произведение векторов
Векторное и смешанное произведение векторов Методичні основи вивчення часу і одиниць його вимірювання
Методичні основи вивчення часу і одиниць його вимірювання Алгебраические дроби (7 класс)
Алгебраические дроби (7 класс) Табличний симплекс-метод
Табличний симплекс-метод Конус. Задание на самоподготовку
Конус. Задание на самоподготовку Решение систем линейных уравнений. Правило Крамера. Метод Гаусса. Матричный метод
Решение систем линейных уравнений. Правило Крамера. Метод Гаусса. Матричный метод Прямоугольный параллелепипед
Прямоугольный параллелепипед Геометрия. Конспекты
Геометрия. Конспекты Перпендикуляр и наклонная. Угол между прямой и плоскостью. 10 класс
Перпендикуляр и наклонная. Угол между прямой и плоскостью. 10 класс Индивидуальный проект на тему Золотое сечение в природе
Индивидуальный проект на тему Золотое сечение в природе סדר פעולות החשבון
סדר פעולות החשבון Свойства умножения
Свойства умножения Цилиндр, конус, шар
Цилиндр, конус, шар Дополнительные построения в трапеции при решении задач
Дополнительные построения в трапеции при решении задач Lecture 7
Lecture 7 Закончите предложения
Закончите предложения