Векторы

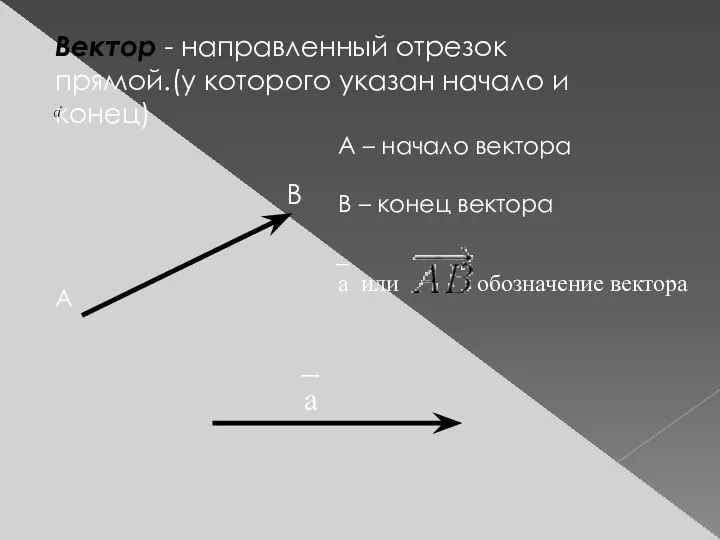
Вектор - направленный отрезок прямой.(у которого указан начало и конец)
В
А
А – начало вектора
В – конец вектора
͢
а
͢
а или обозначение вектора

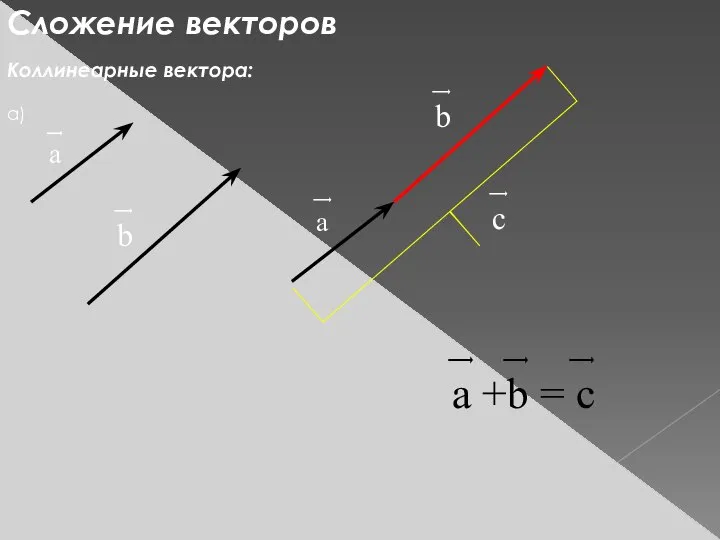
Сложение векторов
Коллинеарные вектора:
͢
а
͢
b
͢
c
͢
b
͢
а
͢ ͢ ͢
а +b = с
а)

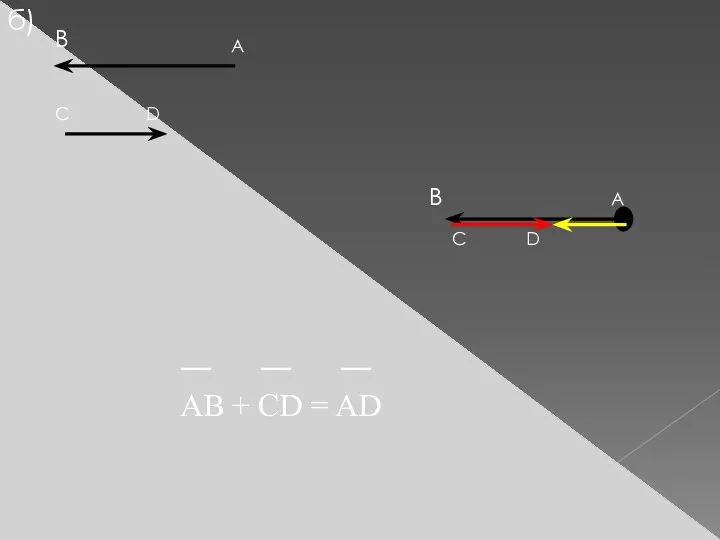
б)
В
А
D
C
А
В
C
D
― ― ―
AB + CD = AD

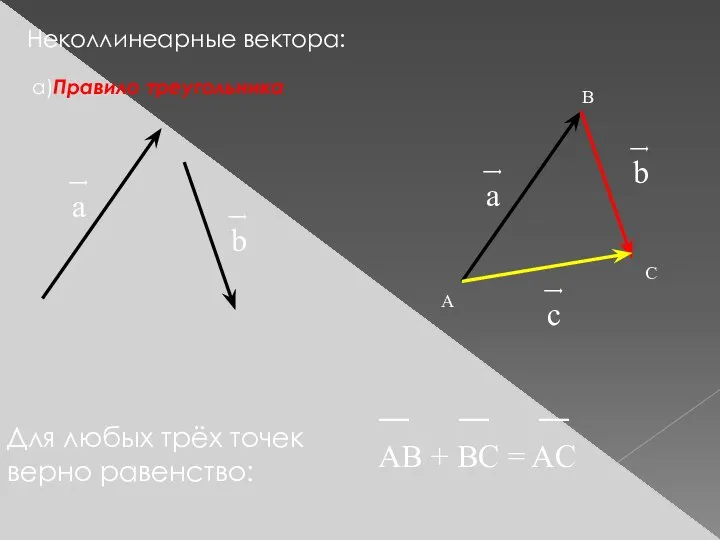
Неколлинеарные вектора:
а)Правило треугольника
͢
а
͢
а
͢
b
͢
b
͢
c
― ― ―
AB + BC = AC
A
B
C
Для любых трёх точек верно равенство:

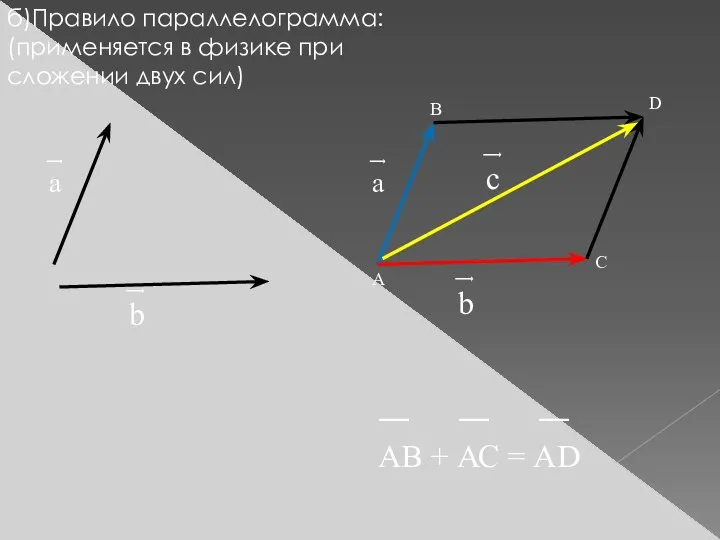
б)Правило параллелограмма: (применяется в физике при сложении двух сил)
͢
а
͢
b
͢
а
͢
b
͢
с
― ― ―
AB + АС = AD
D
А
B
С

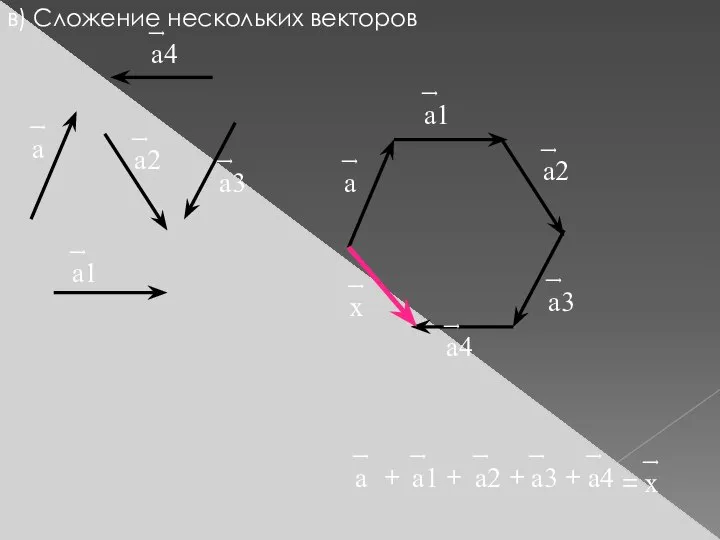
в) Сложение нескольких векторов
͢
а
͢
а1
͢
а2
͢
а3
͢
а4
͢
а
͢
а1
͢
а2
͢
а3
͢
а4
͢
х
͢
а
͢
а1
͢
а2
͢
а3
͢
а4
+
+
+
+
=
͢
х

͢
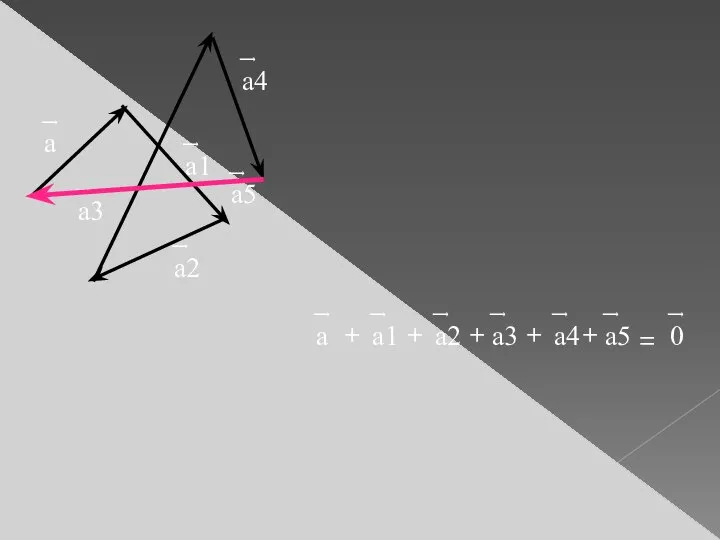
а
͢
а1
͢
а2
͢
а3
͢
а4
͢
а5
͢
а
͢
а1
͢
а2
͢
а3
͢
а4
+
+
+
+
=
͢
0
͢
а5
+

Законы сложения векторов.
Для любых векторов а,b, c справедливы равенства:
͢ ͢ ͢ ͢
а +b= b + a – переместительный закон
͢ ͢ ͢ ͢ ͢ ͢
(а +b)+c=a+(b+c) – сочетательный закон
͢ ͢ ͢
3) а +0 = а – поглощение нулевого вектора

Вычитание векторов.
Разностью двух векторов а и b называется вектор с , сумма которого с вектором b равняется вектору а.
͢ ͢ ͢
а -b = с ?
͢ ͢ ͢
c+b = a

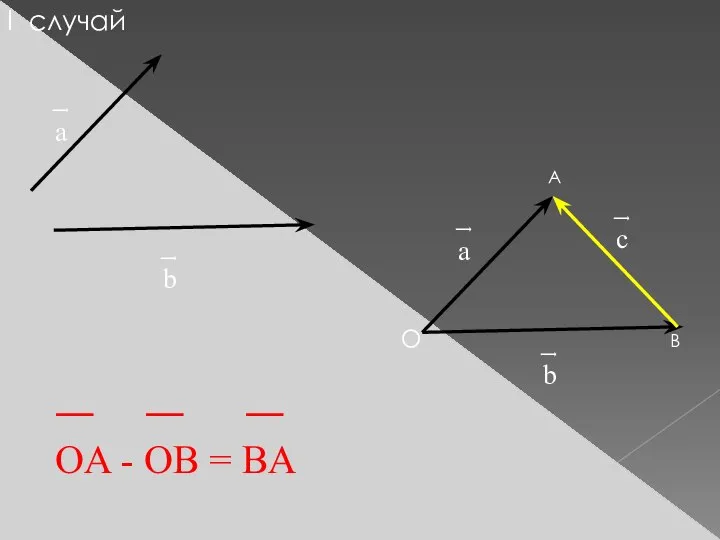
I случай
͢
а
͢
b
͢
а
͢
b
͢
c
O
A
B
― ― ―
OA - OB = BA

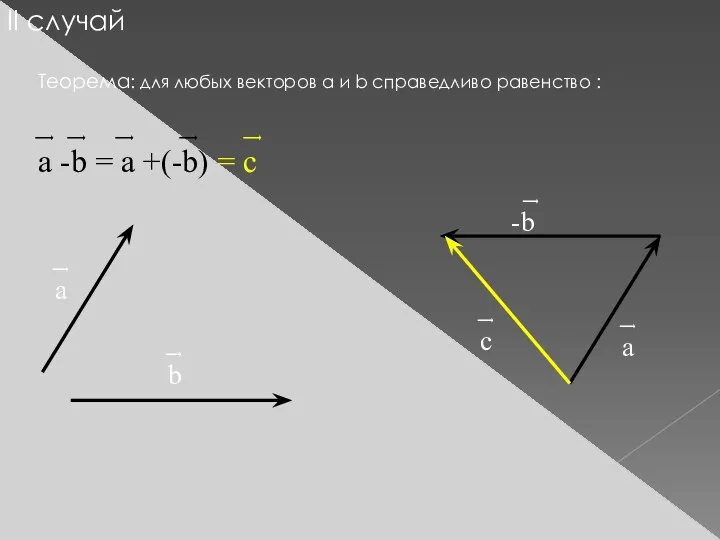
II случай
Теорема: для любых векторов а и b справедливо равенство :
͢ ͢ ͢ ͢ ͢
а -b = а +(-b) = c
͢
а
͢
b
͢
c
͢
а
͢
-b

Произведение не нулевого вектора любое число k равняется вектору
͢
а на
͢
b
→ →
b= a * k
→ →
1)│ b│= │a │* │k│
→ →
2)если k > 0 => b ↑↑ a
→ →
если k < 0 => b ↑↓ a
→ →
если k = 0 => b = 0

Свойства умножения вектора на число.
→ →
1)(m * n) * a = m * (a * n) – сочетательный
→ → →
2)(m+n) * a = m*a + n*a – I распределительный
→ → → →
3)(a+b) * m=m*a + m*b – II распределительный
→ → →
4)0 * a = m*0 = 0 – поглощение нуля и нулевого вектора