Содержание
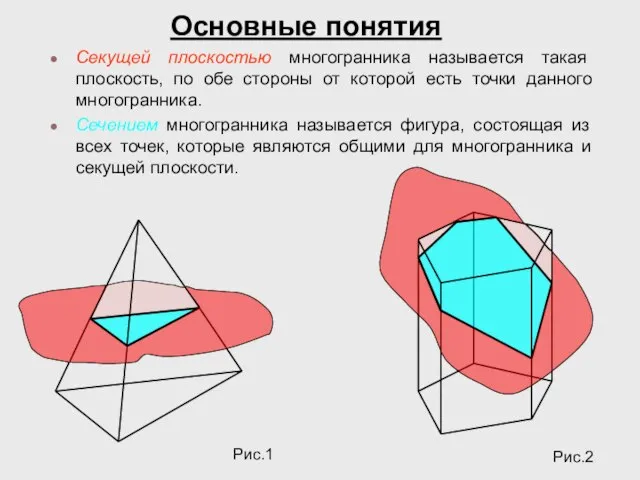
- 2. Секущей плоскостью многогранника называется такая плоскость, по обе стороны от которой есть точки данного многогранника. Сечением
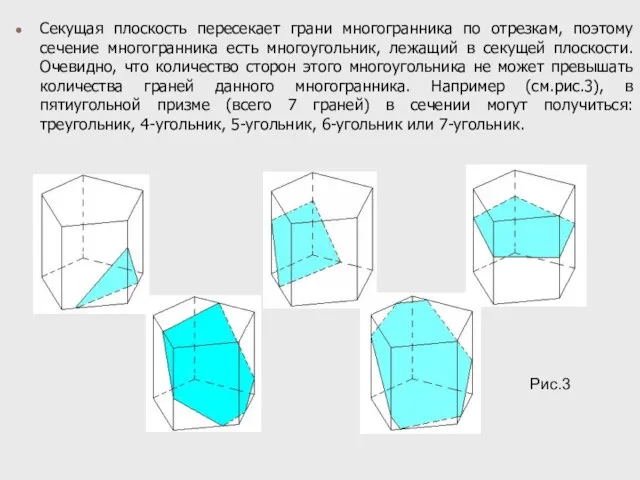
- 3. Секущая плоскость пересекает грани многогранника по отрезкам, поэтому сечение многогранника есть многоугольник, лежащий в секущей плоскости.
- 4. Две плоскости пересекаются по прямой (эта аксиома и дала названию метода – под «следом» понимается прямая
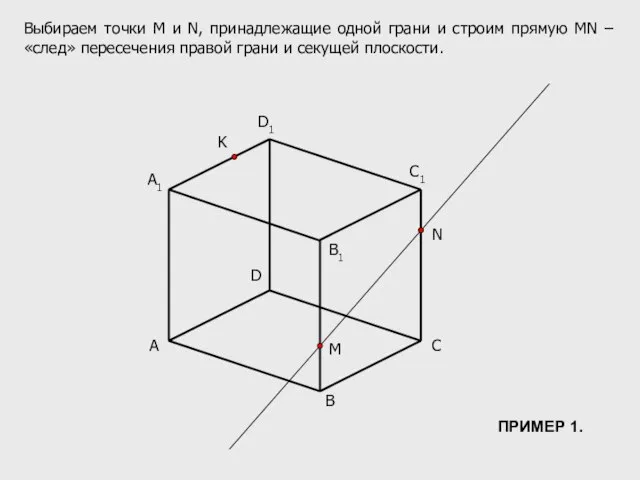
- 5. A B C D B1 C1 D1 M N K Выбираем точки М и N, принадлежащие
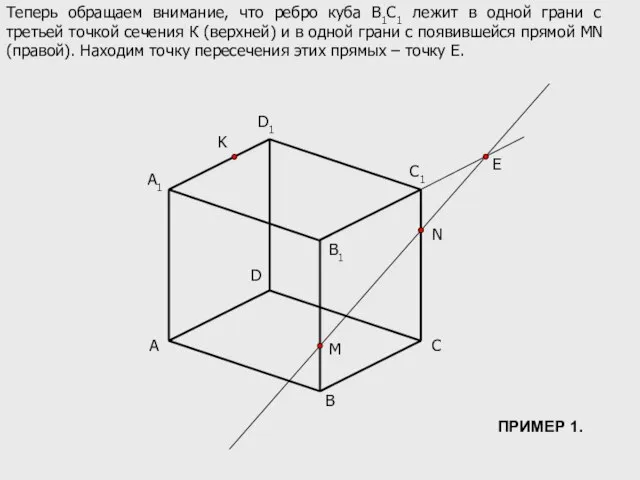
- 6. A B C D B1 C1 D1 M N K A1 E Теперь обращаем внимание, что
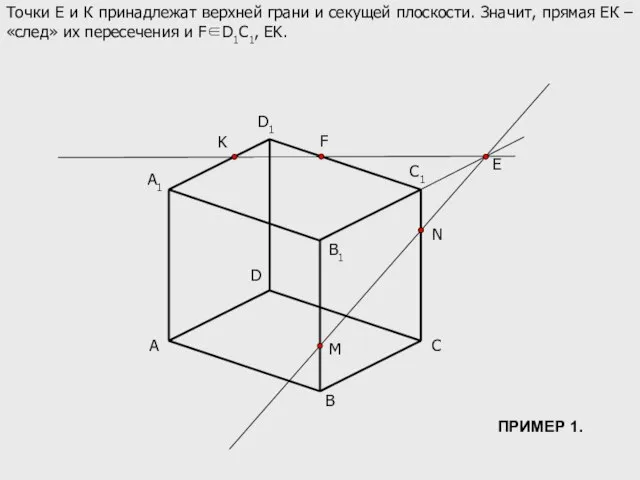
- 7. A B C D B1 C1 D1 M N K A1 E Точки Е и К
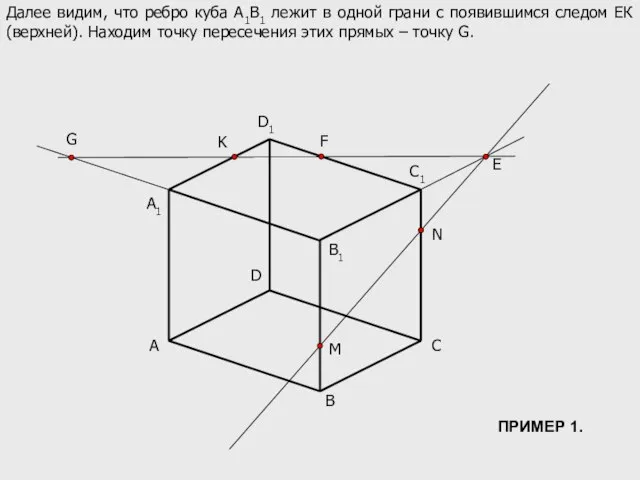
- 8. A B C D B1 C1 D1 M N K A1 E F Далее видим, что
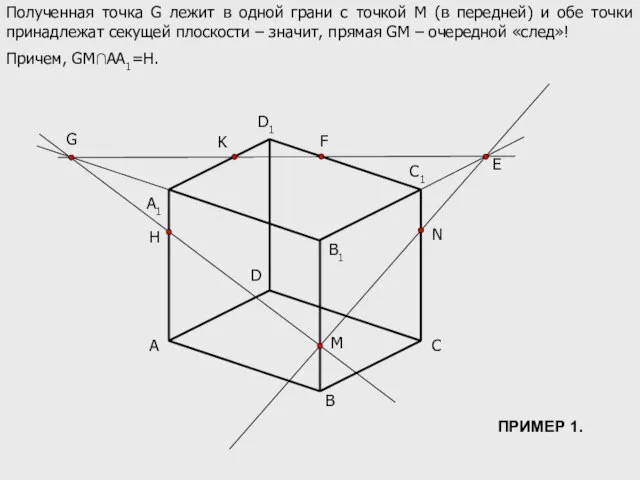
- 9. A B C D B1 C1 D1 M N K A1 E F G Полученная точка
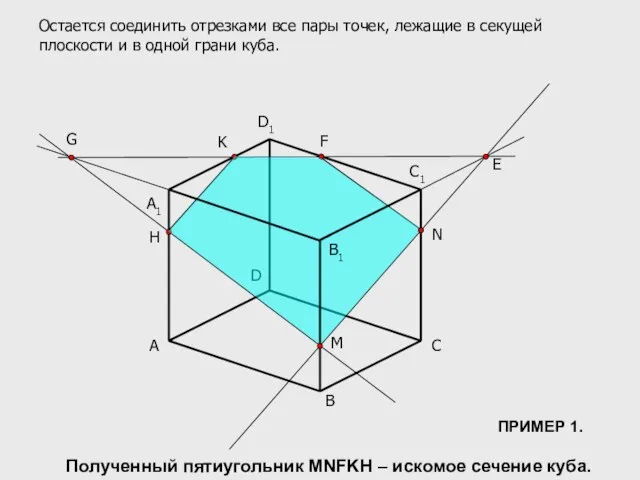
- 10. A B C D C1 D1 M N K A1 E F G H Остается соединить
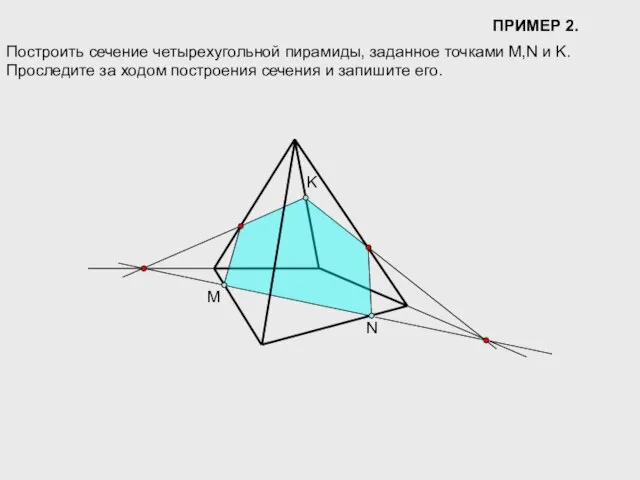
- 11. ПРИМЕР 2. M N K Построить сечение четырехугольной пирамиды, заданное точками M,N и K. Проследите за
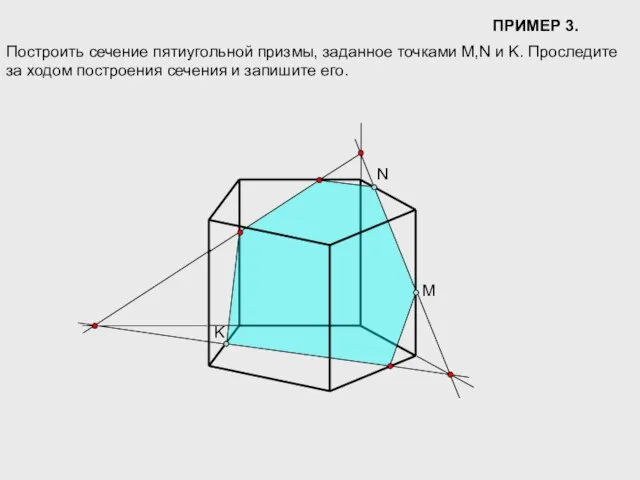
- 12. ПРИМЕР 3. Построить сечение пятиугольной призмы, заданное точками M,N и K. Проследите за ходом построения сечения
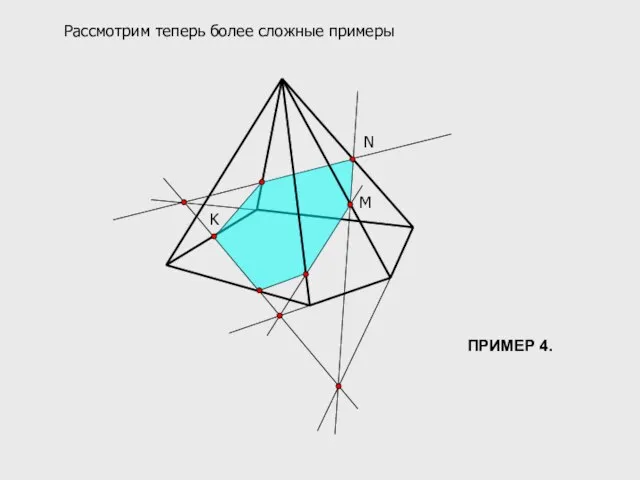
- 13. M N K Рассмотрим теперь более сложные примеры ПРИМЕР 4.
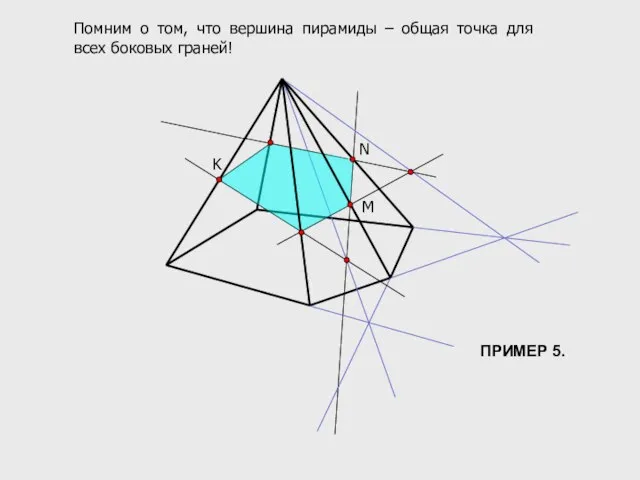
- 14. M N K Помним о том, что вершина пирамиды – общая точка для всех боковых граней!
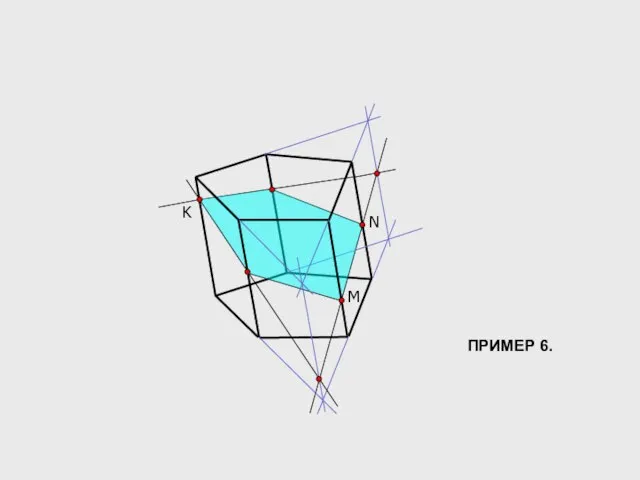
- 15. K M N ПРИМЕР 6.
- 16. Плоскость сечения может задаваться: 1) тремя точками, не лежащими на одной прямой; 2) прямой и точкой,
- 18. Скачать презентацию


 Прямая и плоскость в пространстве
Прямая и плоскость в пространстве Решение задач
Решение задач Простейшие геометрические уравнения
Простейшие геометрические уравнения Геометрическая мозаика из правильных одноимённых многоугольников
Геометрическая мозаика из правильных одноимённых многоугольников Обработка экспериментальных данных. Описательная статистика: основные понятия
Обработка экспериментальных данных. Описательная статистика: основные понятия Окружность и её элементы
Окружность и её элементы Формулы двойного угла
Формулы двойного угла Экскурсия в мир чисел
Экскурсия в мир чисел Параллельные прямые в пространстве
Параллельные прямые в пространстве Действительный анализ. Интеграл Римана и критерий Лебега
Действительный анализ. Интеграл Римана и критерий Лебега Сфера
Сфера Многогранники
Многогранники Определенный интеграл. Пример 2. Лекция
Определенный интеграл. Пример 2. Лекция Логарифмические уравнения (часть 2)
Логарифмические уравнения (часть 2) Правила комбинаторики. Практическое занятие
Правила комбинаторики. Практическое занятие Презентация на тему Теорема Фалеса
Презентация на тему Теорема Фалеса  Смежные углы
Смежные углы Занимательная математика
Занимательная математика Системы линейных уравнений
Системы линейных уравнений Применение интеграла в физике и геометрии
Применение интеграла в физике и геометрии Сумма углов в треугольнике
Сумма углов в треугольнике Логика и математическая логика. История логики. Алгебра высказываний
Логика и математическая логика. История логики. Алгебра высказываний Сложение и вычитание дробей
Сложение и вычитание дробей Правильные многогранники
Правильные многогранники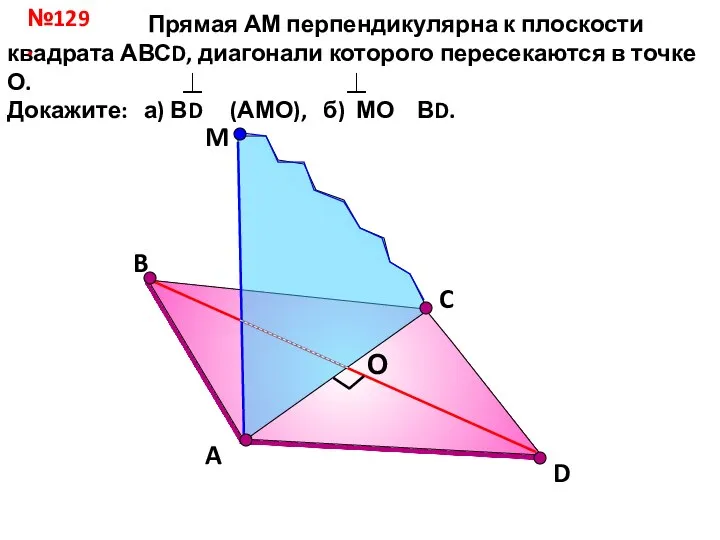 Прямая АМ перпендикулярна к плоскости квадрата АВСD. урок 29
Прямая АМ перпендикулярна к плоскости квадрата АВСD. урок 29 Сложение вида +2, +3
Сложение вида +2, +3 Презентация по математике "Основы концепции “глубинного анализа текстов" -
Презентация по математике "Основы концепции “глубинного анализа текстов" -  Учимся писать цифры
Учимся писать цифры