Содержание
- 2. Замечательно, что наука, которая начала с рассмотрения азартных игр, обещает стать наиболее важным объектом человеческого знания.
- 3. Событие – это результат испытания. Что такое событие? Из урны наудачу берут один шар. Извлечение шара
- 4. Непредсказуемые события называются случайными . В жизни мы постоянно сталкиваемся с тем, что некоторое событие может
- 5. Два события, которые в данных условиях могут происходить одновременно, называются совместными, а те, которые не могут
- 6. Равновозможными называются события, когда в их наступлении нет преимуществ. Неравновозможные события те, у которых в наступлении
- 7. Событие, которое происходит всегда, называют достоверным. Событие, которое не может произойти, называется невозможным. Пусть, например, из
- 8. Классическое определение вероятности. Вероятностью события А при проведении некоторого испытания называют отношение числа тех исходов, в
- 9. Алгоритм нахождения вероятности случайного события. Для нахождения вероятности случайного события А при проведении некоторого испытания следует
- 10. Пример. На завод привезли партию из 1000 подшипников. Случайно в эту партию попало 30 подшипников, не
- 11. Для вычисления вероятности часто используют правило умножения. Для того, чтобы найти число всех возможных исходов независимого
- 12. Свойство вероятностей противоположных событий. События А и В называются противоположными, если всякое наступление события А означает
- 13. Пример. 1. Бросаем один раз игральную кость. Событие А – выпадение четного числа очков, тогда событие
- 14. 2. В среднем из 1000 аккумуляторов, поступивших в продажу, 6 неисправны. Найдите вероятность того, что один
- 15. Решение задач. 1. Монета бросается два раза. Какова вероятность того, что: а) герб выпадет хотя бы
- 16. 2. Игральная кость бросается два раза. Какова вероятность того, что сумма выпавших очков равна 6 ?
- 17. 3. В ящике лежат 6 красных и 6 синих шаров. Наудачу вынимают 8 шаров. Определите вероятность
- 18. 4. Научная конференция проводится 3 дня. Всего запланировано 50 докладов: в первый день – 30 докладов,
- 19. 5. Перед началом первого тура чемпионата по теннису разбивают на игровые пары случайным образом с помощью
- 20. Итог урока Домашнее задание: выполнить онлайн тест по адресу http://gomonova.ucoz.ru/index/test/0-32.
- 22. Скачать презентацию



















 Параллельные плоскости
Параллельные плоскости Приёмы умножения на 2
Приёмы умножения на 2 Математика 4 класс
Математика 4 класс Презентация на тему Прибавление и вычитание числа 3
Презентация на тему Прибавление и вычитание числа 3  Математика в профессии Застройщик
Математика в профессии Застройщик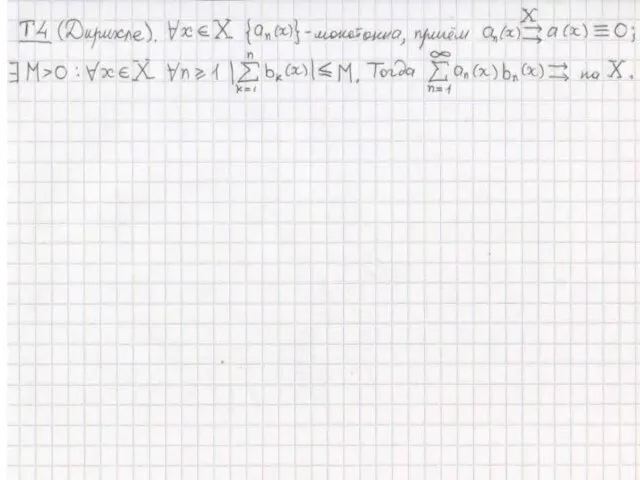 Свойства равномерно-сходящихся плоскостей и рядов
Свойства равномерно-сходящихся плоскостей и рядов Презентация на тему Пропорции
Презентация на тему Пропорции  Перетворення графіків
Перетворення графіків Многогранники. Розв'язування задач
Многогранники. Розв'язування задач Тренажёр. Единицы измерения
Тренажёр. Единицы измерения Обыкновенные дроби
Обыкновенные дроби Устная работа. Вычисления
Устная работа. Вычисления Вычисление реакций и перемещений в статически неопределимых системах
Вычисление реакций и перемещений в статически неопределимых системах Перпендикулярные прямые
Перпендикулярные прямые Функциональная грамотность (математика) - задачи
Функциональная грамотность (математика) - задачи Решение тригонометрических уравнений
Решение тригонометрических уравнений Алгоритм письмового додавання, якщо сума розрядних одиниць дорівнює 10
Алгоритм письмового додавання, якщо сума розрядних одиниць дорівнює 10 Сложение отрицательных чисел
Сложение отрицательных чисел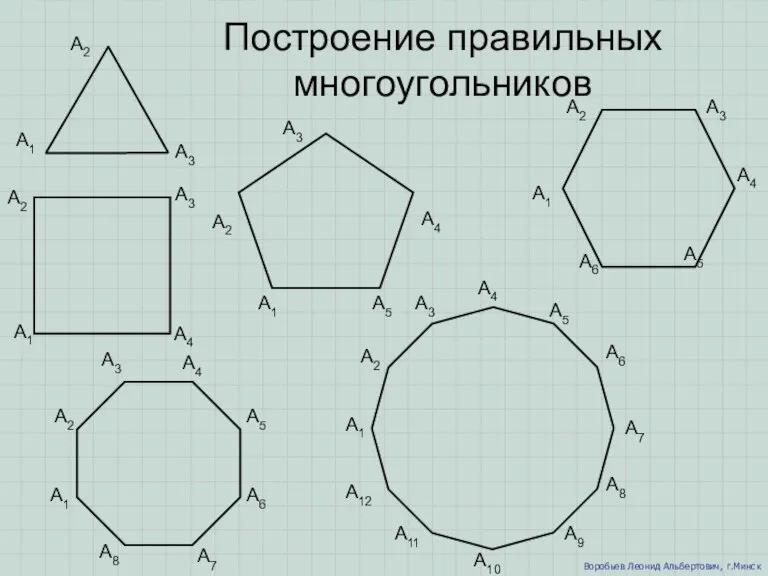 Построение правильных многоугольников
Построение правильных многоугольников Булеві функції. Перетворення логічних виразів. КНФ та ДНФ. СКНФ та СДНФ. Контрольна робота
Булеві функції. Перетворення логічних виразів. КНФ та ДНФ. СКНФ та СДНФ. Контрольна робота Совокупность математических методов для изучения свойств кубика Рубика
Совокупность математических методов для изучения свойств кубика Рубика Золотое сечение. Витрувий
Золотое сечение. Витрувий Презентация на тему Кто хочет стать математиком
Презентация на тему Кто хочет стать математиком  Решение логарифмических уравнений к занятию
Решение логарифмических уравнений к занятию Понятие и виды средних величин
Понятие и виды средних величин Презентация на тему Вклад Пифагора в развитие музыки 7 класс
Презентация на тему Вклад Пифагора в развитие музыки 7 класс  Квадратные неравенства с параметрами
Квадратные неравенства с параметрами Логарифм и его свойства
Логарифм и его свойства