Слайд 2Уравнения, решаемые с помощью условия равенства одноимённых тригонометрических функций
Многие тригонометрические уравнения могут

быть приведены к равенству одноимённых тригонометрических функций.
Такие уравнения решаются на основании условий равенства одноимённых тригонометрических функций, т. е. тех условий, которым должны удовлетворять два угла: α и β, если 1) sin α = sin β, 2) cos α = cos β,
3) tg α = tg β.
Слайд 3Решение уравнения вида sin α = sin β
Для того, чтобы синусы

двух углов были равны, необходимо и достаточно, чтобы:
α – β = 2n или α + β = (2n+1) , где n целое число.
Решить уравнение: sin 3x = sin 5x
Решение. На основании условия равенства двух синусов имеем: 1) 5х-3х = 2κ; 2х = 2κ, х= κ, где κ целое число.
2) 3х+5х = (2κ + 1), х = (2κ+1) ̷ 8, где κ целое число.
Ответ: х= к; х = (2к+1) ̷ 8, где к целое число.
Слайд 5Решение уравнения вида cosx = cosy
Для того чтобы косинусы двух углов были

равны, необходимо и достаточно выполнение одного из следующих условий:
1) х - у = 2n или х + у = 2n, где n-целое число
2) Решить уравнение: cos 3x = cos 5x
Решение: 5х – 3х = 2n,
2х = 2n,
х = n, где n- целое число
или 5х + 3х = 2n,
8х = 2n,
х = ¼ n
Ответ: ¼ n, где n целое число.
Слайд 6Решение уравнения вида tgx = tgy
Для того, чтобы тангенсы двух углов были

равны, необходимо и достаточно одновременное выполнение двух условий: 1) тангенс каждого из двух углов существует;
2) разность этих углов равна числу , умноженному на целое число.
Слайд 7Решить уравнение : tg (5x + ̷ 3) = ctg 3x
Преобразуем

уравнение и получим tg (5x + ̷ 3) = tg ( ̷ 2 – 3x ).
На основании условия равенства тангенсов двух углов имеем:
5x + ̷ 3 - ̷ 2 + 3x = n;
8x = ̷ 6 + n, x = ( 6n +1 ) ̷ 48, где n- целое
число. При каждом значении x из этой
совокупности каждая из частей уравнения
существует.
Ответ: (6n + 1 ) ̷ 48, где n – целое число.
Слайд 8Некоторые виды тригонометрических
уравнений

Слайд 9Уравнения, правая часть которых равна нулю, решаются разложением левой части на множители.

При решении нужно помнить, что произведение равно нулю, если один из множителей равен нулю, а другие множители при этом не теряют смысла.









 Периметр квадрата
Периметр квадрата Тригонометрия. Восхождение на пик
Тригонометрия. Восхождение на пик Ответы к тестам для подготовки к ЕГЭ по математике
Ответы к тестам для подготовки к ЕГЭ по математике Сложение двух векторов
Сложение двух векторов Основные понятия комбинаторики. Факториал. Вычисление факториала
Основные понятия комбинаторики. Факториал. Вычисление факториала Признаки равенства треугольников
Признаки равенства треугольников Урок математики в 3 классе
Урок математики в 3 классе Производная. Правила нахождения производных. Производная степенной функции с действительным показателем
Производная. Правила нахождения производных. Производная степенной функции с действительным показателем Теорема Пифагора. Чертеж к доказательству Пифагора
Теорема Пифагора. Чертеж к доказательству Пифагора Сложение и вычитание многочленов
Сложение и вычитание многочленов Применение производной к построению графиков функций
Применение производной к построению графиков функций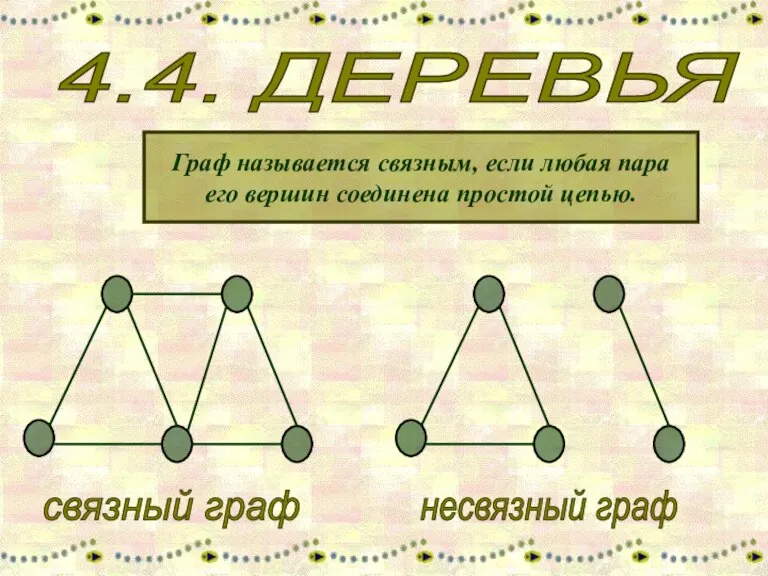 Деревья
Деревья Думаємо колективно, працюємо оперативно, сперечаємось доказово – це для всіх обов'язково
Думаємо колективно, працюємо оперативно, сперечаємось доказово – це для всіх обов'язково Интегрирование неотрицательніх измериміх функций
Интегрирование неотрицательніх измериміх функций ТРАПЕЦІЯ
ТРАПЕЦІЯ Решение задач на работу
Решение задач на работу Решение простейших логарифмических неравенств
Решение простейших логарифмических неравенств Алгоритм решения линейных уравнений
Алгоритм решения линейных уравнений Угол. Прямой и развернутый угол. Чертежный треугольник
Угол. Прямой и развернутый угол. Чертежный треугольник Площадь треугольника
Площадь треугольника Функции многих переменных. Лекция 16
Функции многих переменных. Лекция 16 Цилиндр. Круговой цилиндр
Цилиндр. Круговой цилиндр Метод геометрических рядов и точные решения дифференциально-разностных уравнений
Метод геометрических рядов и точные решения дифференциально-разностных уравнений Использование свойств действий при вычислениях. Наглядный материал к уроку
Использование свойств действий при вычислениях. Наглядный материал к уроку Презентация по математике "Дроби в Древнем Риме" -
Презентация по математике "Дроби в Древнем Риме" -  Линейная функция. Задания
Линейная функция. Задания Навыки решения составных задач
Навыки решения составных задач Решение треугольников
Решение треугольников