Содержание
- 2. Содержание Введение................................................... .......3-5слайд Начало изучения..............................................6-7 слайд Этапы изучения...................................................8 слайд Группы функций...................................................9 слайд Определение и график синуса..........................10
- 3. В древности тригонометрия возникла в связи с потребностями астрономии, землемерия и строительного дела, то есть носила
- 4. В настоящее время изучению тригонометрических функций именно как функций числового аргумента уделяется большое внимание в школьном
- 5. Кроме того, большие трудности при изучении темы «Тригонометрические функции» в школьном курсе возникают из-за несоответствия между
- 6. Таким образом, основной целью создания данной работы является изучение темы: «Тригонометрические функции» в курсе алгебры и
- 7. Тригонометрические функции — математическиематематические функции от угла. Они важны при изучении геометрии, а также при исследовании
- 8. В изучении тригонометрических функций можно выделить следующие этапы: I. Первое знакомство с тригонометрическими функциями углового аргумента
- 9. Существует несколько способов определения тригонометрических функций. Их можно подразделить на две группы: аналитические и геометрические. К
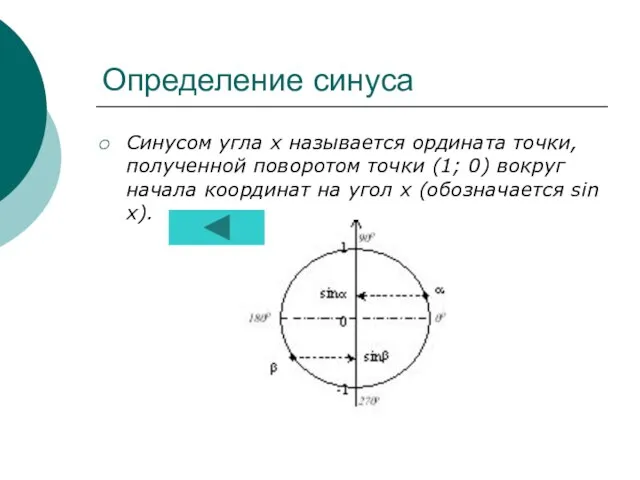
- 10. Определение синуса Синусом угла х называется ордината точки, полученной поворотом точки (1; 0) вокруг начала координат
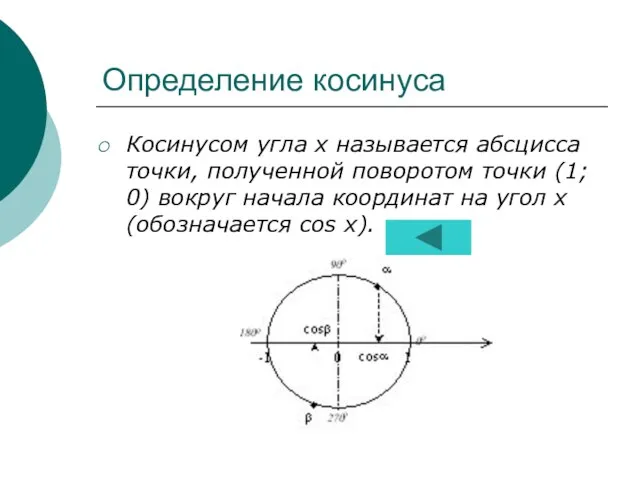
- 11. Определение косинуса Косинусом угла х называется абсцисса точки, полученной поворотом точки (1; 0) вокруг начала координат
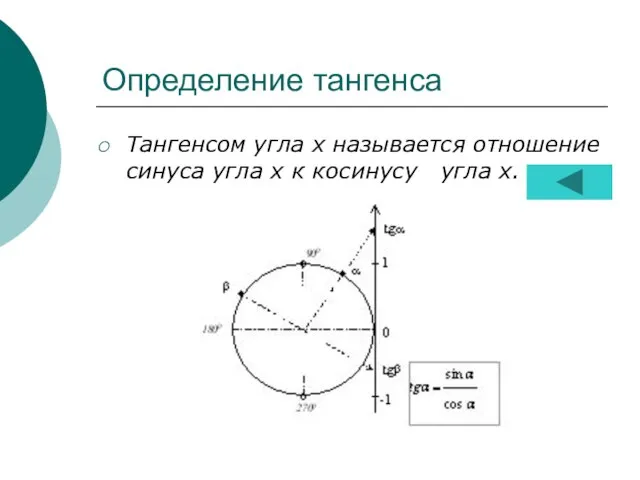
- 12. Определение тангенса Тангенсом угла х называется отношение синуса угла х к косинусу угла х.
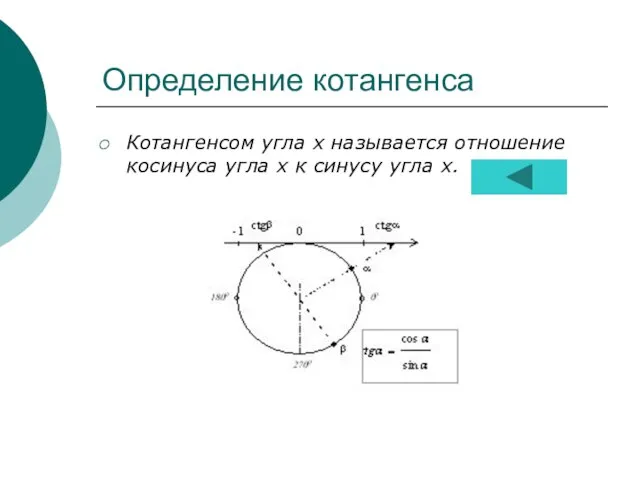
- 13. Определение котангенса Котангенсом угла х называется отношение косинуса угла х к синусу угла х.
- 14. Обратные тригонометрические функции. Для sin х, cos х, tg х и ctg х можно определить обратные
- 15. А это основные тригонометрические формулы, которыми пользуются учащиеся во время решения тригонометрических задач.
- 17. Тригонометрия- это наука, о которой можно говорить, рассказывать и писать БЕСКОНЕЧНО! Это одна из составляющих наук
- 18. Используемая литература: А.Н.Колмогоров, А.М.Абрамов «Алгебра и начала анализа». Ю.М.Колягин, Ю.В.Ткачёв «Алгебра и начала анализа». Г.Бирюков, А.А.Бряндинская
- 20. Скачать презентацию













 Презентация на тему ДЕЛЕНИЕ
Презентация на тему ДЕЛЕНИЕ  Презентация на тему Составление и решение задач разного типа различными способами
Презентация на тему Составление и решение задач разного типа различными способами  Параллельные прямые. Тест
Параллельные прямые. Тест Понятие дифференциала. Приложение дифференциала
Понятие дифференциала. Приложение дифференциала Основы тригонометрии
Основы тригонометрии Презентация на тему Простейшая геометрия
Презентация на тему Простейшая геометрия  Затухающий гармонический осциллятор. Лекция 3
Затухающий гармонический осциллятор. Лекция 3 Логика высказываний и булевы алгебры (Boolean Algebra and Logic)
Логика высказываний и булевы алгебры (Boolean Algebra and Logic) Четырехугольник . Прямоугольник. Квадрат
Четырехугольник . Прямоугольник. Квадрат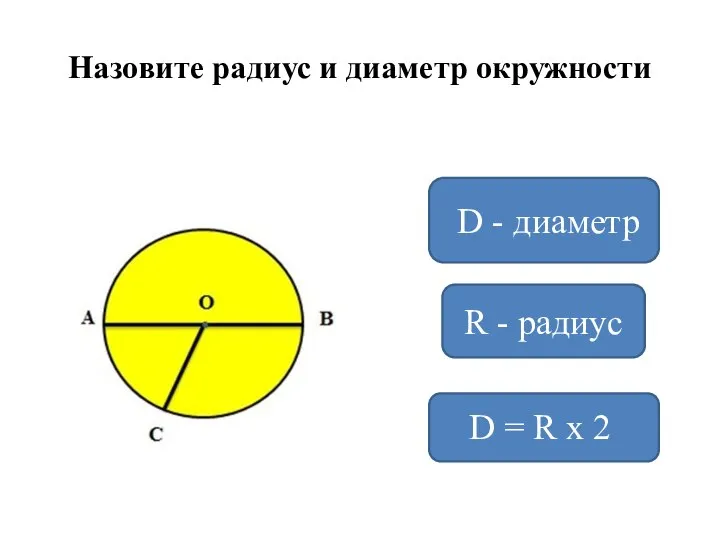 Радиус и диаметр окружности
Радиус и диаметр окружности Бином Ньютона. Треугольник Паскаля
Бином Ньютона. Треугольник Паскаля Обобщение по 3-м формулам сокращенного умножения
Обобщение по 3-м формулам сокращенного умножения Координаты и векторы
Координаты и векторы Вероятность и статистика
Вероятность и статистика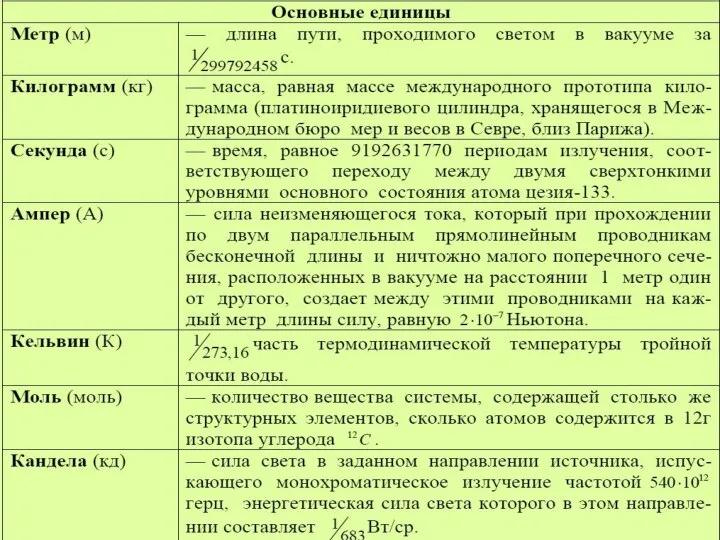 Основные единиціы
Основные единиціы Линейная алгебра. Матрицы. Основные понятия. Действия над матрицами. Поиск обратной матрицы
Линейная алгебра. Матрицы. Основные понятия. Действия над матрицами. Поиск обратной матрицы Решение задач на проценты. Концентрация
Решение задач на проценты. Концентрация Сложение и вычитание рациональных чисел
Сложение и вычитание рациональных чисел Уравнение средней
Уравнение средней Надежность технических систем
Надежность технических систем Квадратные уравнения
Квадратные уравнения Число. Натуральный ряд. Абсолютная шкала измерений
Число. Натуральный ряд. Абсолютная шкала измерений Построение сечений тетраэдра и параллелепипеда
Построение сечений тетраэдра и параллелепипеда Ситуация успеха на уроках математики как средство повышения качества образования
Ситуация успеха на уроках математики как средство повышения качества образования Умножение дробей на натуральное число
Умножение дробей на натуральное число Формулы дифференцирования
Формулы дифференцирования Длина окружности
Длина окружности Многозначные числа. Тест
Многозначные числа. Тест