Математическая логика

Считается, что первые работы по логике появились в V в. до н. э.
Впервые как самостоятельную теорию ее оформил греческий философ Аристотель в своем труде «Аналитики», где систематизировал известные до него сведения, и эта система впоследствии стала называться формальной логикой.
С этого времени формальная логика просуществовала без особых изменений почти двадцать столетий.
Впоследствии возникла идея и о том, что, записав исходные рассуждения формулами, похожими на математические, можно заменить все цепочки логического вывода формальными «вычислениями».
В Средние века даже делались попытки создания машин «логического вывода».
Развитие математики выявило недостатки логики, разработанной Аристотилем, и потребовало дальнейшего ее развития.
Историческая справка

Введение строения логики на математической основе была предложена немецким математиком Г. Лейбницем, который считал, что основные понятия логики возможно обозначить символами, соединяющимися по особым правилам, что позволит всякое рассуждение заменить вычислением.
Первая реализация идей Лейбница принадлежит английскому ученому Дж. Булю (середина XIX в.), создавшему алгебру, в которой буквами обозначены высказывания.
Его алгебра получила название алгебры высказываний. Введение в логику символических обозначений послужило основой для создания новой науки — математической логики.
Применение математики к логике позволило представить логические теории в новой удобной форме и использовать вычислительный аппарат в решении задач, ранее практически недоступных человеческому мышлению, что существенно расширило область логических исследований.
Функции алгебры логики называются также булевыми функциями, двоичными функциями или переключательными функциями.

Курсовая работа
по дисциплине ″Математическая логика″
Закрепление практических навыков при решении задачи синтеза комбинационных схем.
В качестве критерия эффективности синтезируемой схемы в рамках курсовой работы принята цена схемы по Квайну. Решение задач минимизации, факторизации и декомпозиции булевых функций.
Для решения задачи минимизации применяются два метода: метод Квайна-Мак-Класки, основанный на кубическом представлении булевых функций и являющийся формализованным, и метод минимизирующих карт (карт Карно), который в большой степени является интуитивным.
В курсовой работе в качестве исходной задается не полностью определенная булева функция от пяти переменных. Итогом курсовой работы являются комбинационные схемы, реализующие заданную функцию. Часть схем строится с учетом ограничения на коэффициент объединения по входам. Для каждой схемы определяются цена схемы по Квайну и задержка и проводится анализ схемы путем определения ее реакции на нескольких произвольных наборах входных сигналов.

1. Множества
Множеством называется собрание, совокупность объектов, объединенных по какому-нибудь общему признаку, свойству. Например: множество студентов одной группы, множество целых чисел.
Объекты, из которых состоит множество, называются его элементами.
Множества обозначаются прописными (заглавными) буквами латинского алфавита. Например: A, B, C,…, X, Y,…
Элементы множества обозначаются строчными (малыми) буквами латинского алфавита. Например: a, b, c,…, x, y,…, a1, a2,…
Множества бывают: конечные, бесконечные и пустые.
Например: множество букв русского алфавита конечно. Множество целых чисел бесконечно. Множество целых корней уравнения 2x +5=0 пустое.
Множество, не содержащее ни одного элемента, называется пустым и обозначается знаком ∅.
Объекты, входящие во множество, определенные. Это означает, что для каждого объекта можно однозначно сказать, принадлежит ли он данному множеству или нет.
Объекты, входящие во множество, различимы между собой. Следовательно, во множестве не может быть двух или более одинаковых объектов.
Все объекты, входящие во множество, мыслятся как единое целое. Этим подчеркивается, что все объекты рассматриваются в совокупности, а от свойств отдельных объектов абстрагируются.
ВВЕДЕНИЕ В ТЕОРИЮ МНОЖЕСТВ

1.1. Способы задания множеств
Конечное множество может быть задано перечислением входящих в него и разделенных запятой элементов, например: A = {a1, a2, ... , an}, множество В решений уравнения x2 - 6x + 5 = 0 можно записать так: В = {1, 5}.
Любое множество может быть задано при помощи правила, позволяющего определить, является ли данный объект элементом множества или нет. Например: Множество целых чисел на отрезке от 1 до 5 запишется следующим образом: C = {z│1≤ z ≤ 5, z Є Z}. Множество натуральных чисел, больше 10: X = {x│x >10, x Є N}.
1.2. Подмножества
Множество B называется подмножеством множества A, если каждый элемент B одновременно является и элементом множества A, обозначается знаком ⊂ (В ⊂ А). Например: A = {2, 4, 6, 8, 10}, B = {4, 6, 8}. B есть подмножество A, т.е. B ⊂ A.
Множества, которые состоят из одних и тех же элементов называют равными. Например, C = {x; y; z}, D = {x; y; z} и записывают C = D.

Зафиксированное каким-либо образом множество объектов, допустимых при данном рассмотрении, называют универсальным или универсумом. Будем обозначать данное множество буквой U.
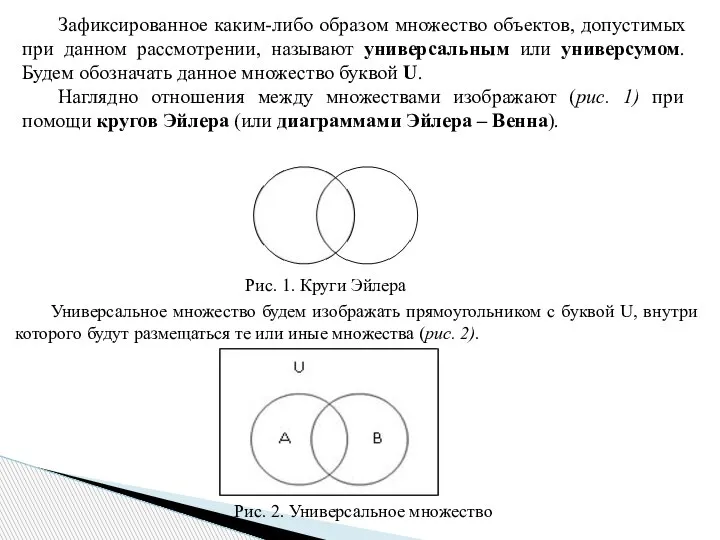
Наглядно отношения между множествами изображают (рис. 1) при помощи кругов Эйлера (или диаграммами Эйлера – Венна).
A B
Рис. 1. Круги Эйлера
Универсальное множество будем изображать прямоугольником с буквой U, внутри которого будут размещаться те или иные множества (рис. 2).
Рис. 2. Универсальное множество

1.3. Операции над множествами
Объединением двух множеств А и В называется такое множество С, которое состоит из всех тех элементов, которые принадлежат хотя бы одному из множеств А или В. Обозначается: A  B, (рис. 3).
С = А  В = {x x  A или x  B}.
Рис. 3. Объединение множеств С = А ∪ В
Например: A = {a, b, c, d, e, f} и
B = {x, y, z}, то C = A ∪ B = {a, b, c, d, e, f, x, y, z}.
Если А1, А2,…, Аn – несколько множеств, то их объединение это множество C, состоящее из элементов, которые принадлежат хотя бы одному их них:
C = A1 ∪ A2 ∪…∪ An={x ⎪ x∈A1 или x∈A2 или …или x∈An}.