Сфера описанная или вписанная

Описанные шары
Шар называется описанным около многогранника, а многогранник вписанным в этот шар, если все вершины многогранника лежат на поверхности шара.
Чтобы около многогранника можно было описать сферу, необходимо и достаточно,
чтобы каждая его грань была многогранником, около которого можно было описать окружность.

Многогранники, вписанные в шар
Центр описанного около многогранника шара есть точка, равноудаленная от всех его вершин. Геометрическое место точек, равноудаленных от всех вершин какой-либо грани, есть прямая, перпендикулярная к плоскости грани и проходящая через центр описанной около нее окружности.
Геометрическое место точек, равноудаленных от концов какой-либо ребра, есть плоскость, перпендикулярная ребру и проходящая через его середину. Значит, центр шара принадлежит одновременно двум указанным геометрическим местам

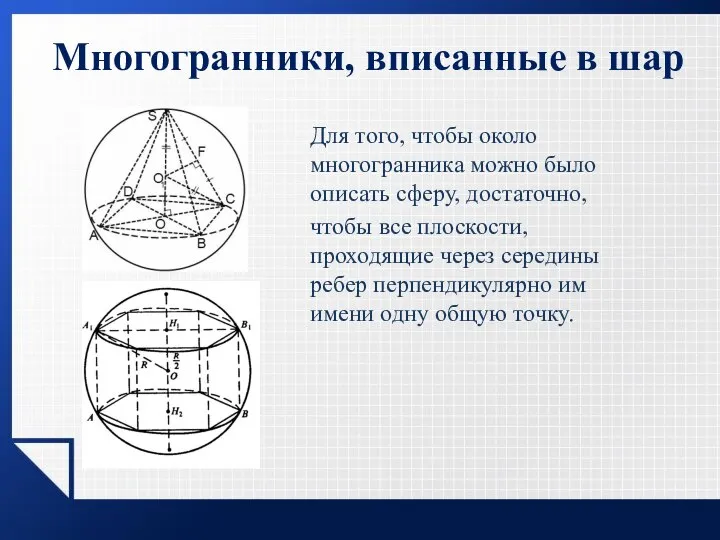
Для того, чтобы около многогранника можно было описать сферу, достаточно,
чтобы все плоскости, проходящие через середины ребер перпендикулярно им имени одну общую точку.
Многогранники, вписанные в шар

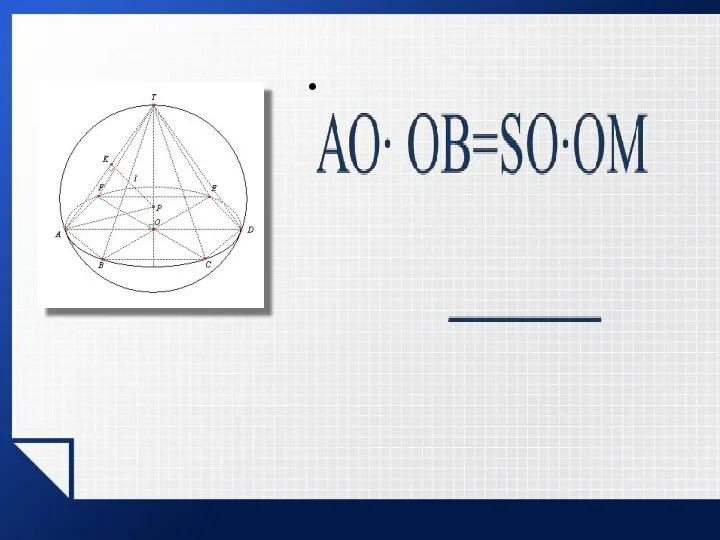
Вписанная пирамида
Для того, чтобы около пирамиды можно было описать сферу, необходимо и достаточно,
чтобы около основания пирамиды можно было описать окружность.

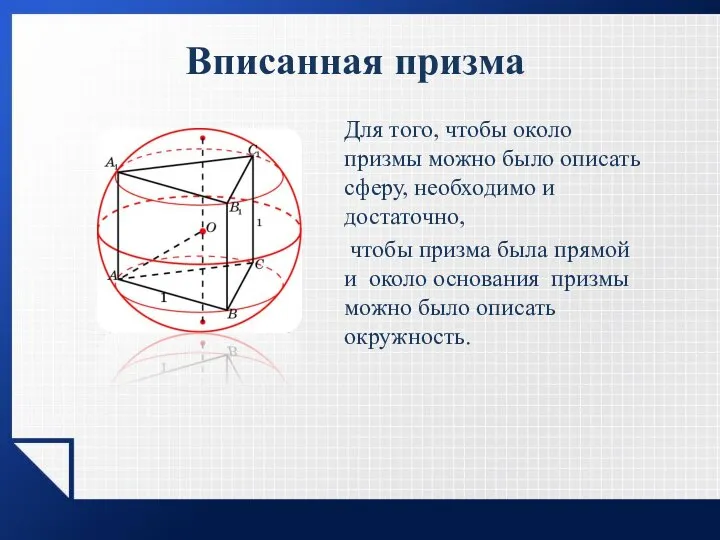
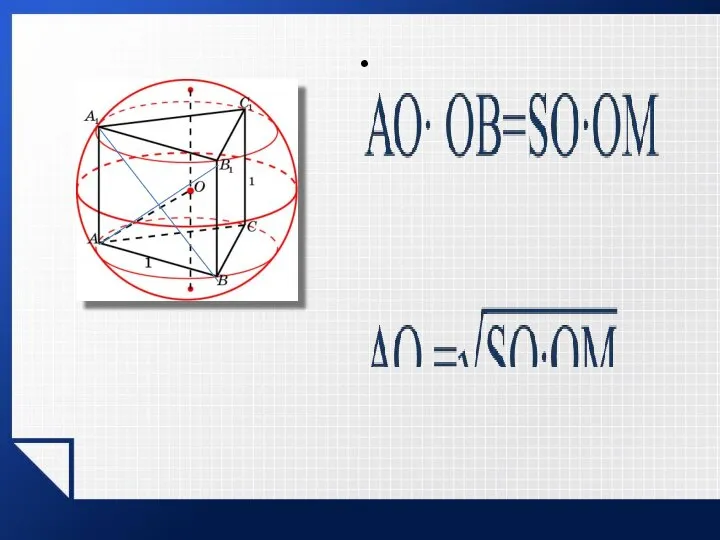
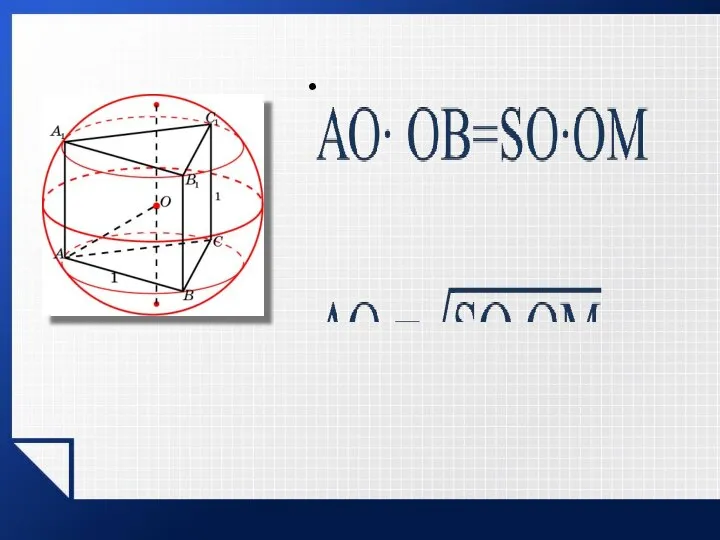
Вписанная призма
Для того, чтобы около призмы можно было описать сферу, необходимо и достаточно,
чтобы призма была прямой и около основания призмы можно было описать окружность.

Вписанный конус
Для того, чтобы около конуса можно было описать сферу, необходимо и достаточно,
( без условий)
Шар называется описанным около конуса, если поверхность шара проходит через вершину конуса, а окружность основания конуса лежит на поверхности шара.

Вписанный цилиндр
Для того, чтобы около цилиндра можно было описать сферу, необходимо и достаточно,
( без условий)
Шар называется описанным около цилиндра , если окружности его оснований лежат на поверхности шара.

Вписанный конус или
шар, описанный около конуса
А
В

Задача 1
Около конуса описан шар. Найти радиус основания конуса, если его высота равна 15 см, а радиус сферы равен 10 см.

Задача 2
Найти радиус описанной около основания окружности в треугольной пирамиде, если высота пирамиды 20 см, а радиус описанной сферы, равен 15 см.
М
К

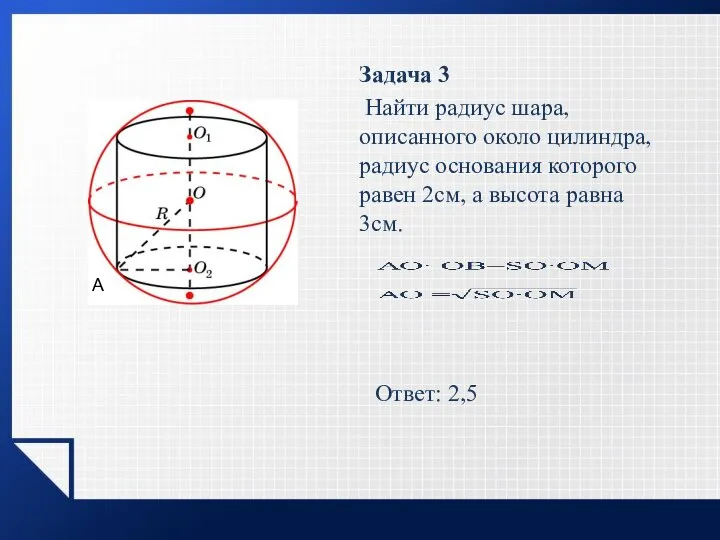
Задача 3
Найти радиус шара, описанного около цилиндра, радиус основания которого равен 2см, а высота равна 3см.
А
Ответ: 2,5

Задача 4
В правильной треугольной пирамиде сторона основания равна 3см, боковые ребра наклонены к плоскости основания под углом 60°. Найти радиус описанной около пирамиды сферы.

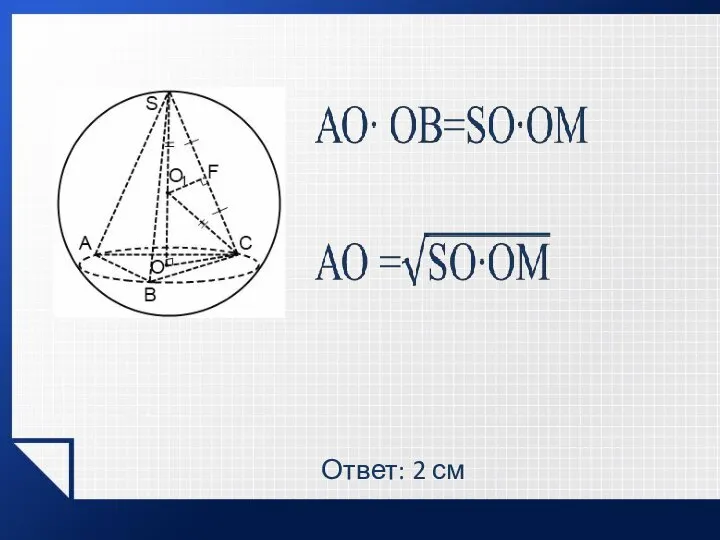
Ответ: 2 см

Вписанные шары
Шар называется вписанным в многогранник, а многогранник- описанным вокруг шара,
если плоскости всех граней касаются шара.

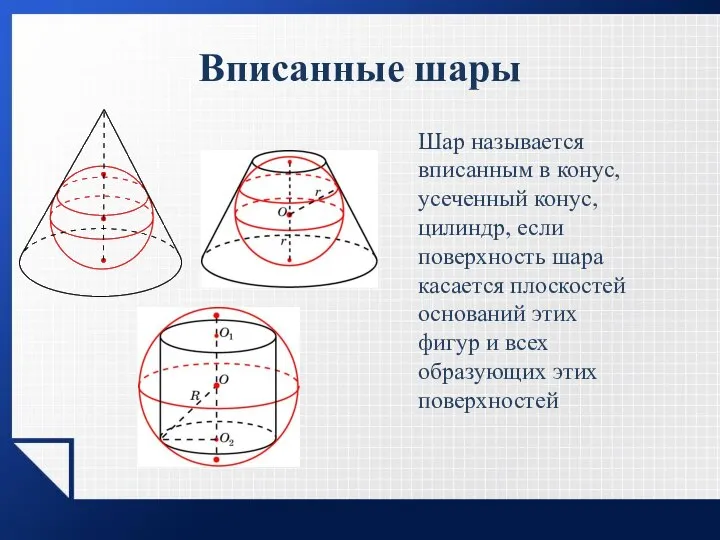
Вписанные шары
Шар называется вписанным в конус, усеченный конус, цилиндр, если поверхность шара касается плоскостей оснований этих фигур и всех образующих этих поверхностей

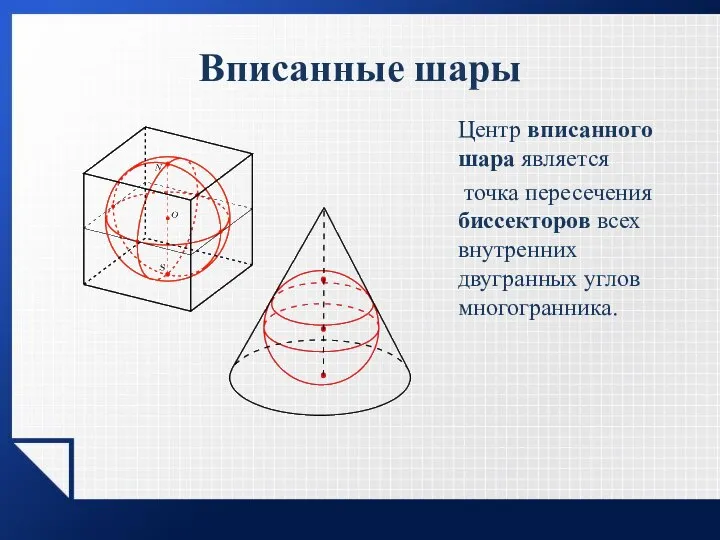
Вписанные шары
Центр вписанного шара является
точка пересечения биссекторов всех внутренних двугранных углов многогранника.

Центр вписанной сферы является точка пересечения биссекторов всех внутренних двугранных углов многогранника.

Шар, вписанный в призму
Для того, чтобы в призму можно было вписать шар, необходимо и достаточно, чтобы в перпендикулярное сечение призмы можно было вписать окружность и чтобы высота призмы была равна диаметру этой окружности.

Шар, вписанный в призму
Шар можно вписать в прямую призму, если в основание призмы можно вписать окружность, а высота призмы равна диаметру этой окружности.
Центр вписанного шара лежит на середине высоты прямой призмы, проходящей через центры окружностей, вписанных в основание призмы.

Шар, вписанный в конус
Центр вписанного в конус шара совпадает с точкой пересечения высоты конуса с биссектрисой угла между любой образующей и плоскостью основания. В конус всегда можно вписать шар и его радиус выражается формулой
l
r
R
R

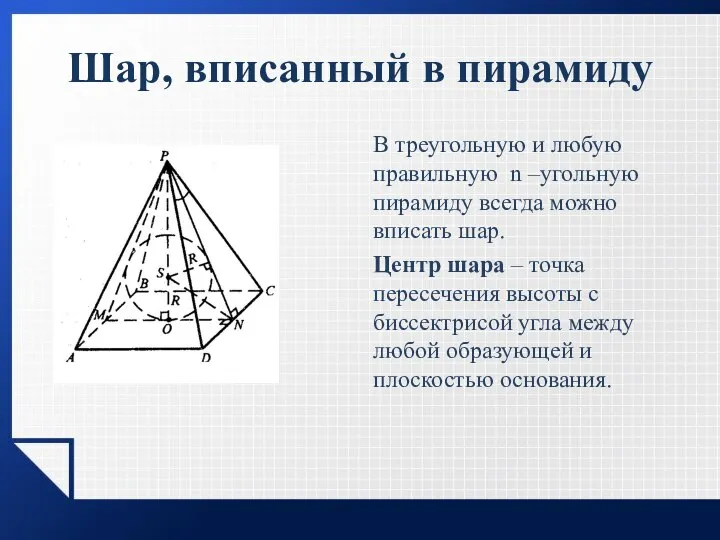
Шар, вписанный в пирамиду
В треугольную и любую правильную n –угольную пирамиду всегда можно вписать шар.
Центр шара – точка пересечения высоты с биссектрисой угла между любой образующей и плоскостью основания.

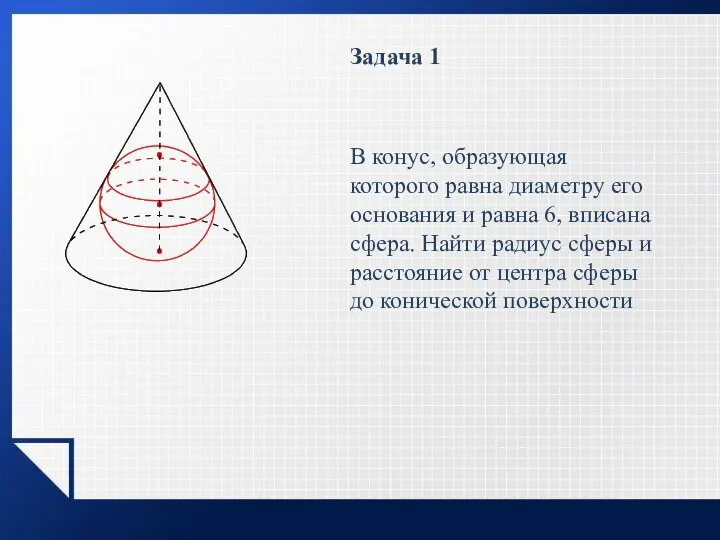
Задача 1
В конус, образующая которого равна диаметру его основания и равна 6, вписана сфера. Найти радиус сферы и расстояние от центра сферы до конической поверхности