Prilozhenie_2_prezentatsia_po_teme_lektsii_5

1. Теория вероятности.
Теория вероятностей - область математики, изучающая закономерности в случайных явлениях.
Случайное явление - это явление, которое при неоднократном воспроизведении одного и того же опыта может протекать каждый раз несколько по-иному.
Опр. (классическое) вероятность события определяется равенством Р(А)=т/п,
где m — число элементарных исходов испытания, благоприятствующих появлению события А; п — общее число возможных элементарных исходов испытания. Предполагается, что элементарные исходы образуют полную группу и равновозможны.
Опр. Относительная частота события А определяется равенством W(A)=m/n
где m —число испытаний. в которых событие А наступило; n — общее число произведенных испытаний.

Опр. (статистическое) в качестве вероятности события принимают его относительную частоту.
Пример: Брошены две игральные кости. Найти вероятность того, что сумма очков на выпавших гранях— четная, причем на грани хотя бы одной из костей появится шестерка.
Решение. На выпавшей грани «первой» игральной кости может появиться одно очко, два очка. .... шесть очков. Аналогичные шесть элементарных исходов возможны при бросании «второй» кости. Каждый из исходов бросания «первой» кости может сочетаться с каждым из исходов бросания «второй». Таким образом, общее число возможных элементарных исходов испытания равно 6 6 = 36. Эти исходы образуют полную группу и в силу симметрии костей равновозможны.
Благоприятствующими интересующему нас событию(хотя бы на одной грани появится шестерка, сумма выпавших очков— четная) являются следующие пять исходов (первым записано число очков, выпавших на «первой» кости, вторым — число очков, выпавших на «второй» кости; далее найдена сумма очков):
1) 6, 2; 6 +2=8, 2) 6, 4; 6+ 4=10, 3) 6, 6; 6+б=12. 4) 2, 6; 2+6=8, 5) 4, 6; 4+6=10.
Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех возможных элементарных исходов: Р = 5/36.

Формула полной вероятности
Вероятность события А, которое может наступить лишь при появлении одного из несовместных событий (гипотез) В1 В2, ..., Вn, образующих полную группу, равна сумме произведений вероятностей каждой из гипотез на соответствующую условную вероятность события А:
Р(А) = Р(В1)РВ1(А) + Р(В2).РВ2(А)+...+Р(Вn)РBn(A) - формула полной вероятности
где Р(В1) + Р(В2)+...+Р(Вn) = 1.

Закон распределения вероятностей дискретной случайной величины.
Опр. Дискретной называют случайную величину, возможные значения которой есть отдельные изолированные числа (т. е. между двумя соседними возможными значениями нет возможных значений), которые эта величина принимает с определенными вероятностями.
Число возможных значений дискретной случайной величины может быть конечным или бесконечным.
Законом распределения дискретной случайной величины называют перечень ее возможных значений и соответствующих им вероятностей. Закон распределения дискретной случайной величины X может быть задан в виде таблицы, первая строка которой содержит возможные значения хi, а вторая—вероятности рi:

Если множество возможных значений X бесконечно (счетно), то ряд p1 + p2+… сходится и его сумма равна единице.
Закон распределения дискретной случайной величины X может быть также задан аналитически (в виде формулы)
P(X=xi)=φ(xi)
Закон распределения дискретной случайной величины можно изобразить графически, для чего в прямоугольной системе координат строят точки M1(x1;p1), M2(x2;p2), …, Mn(xn;pn) (хi; — возможные значения X, рi, — соответствующие вероятности) и соединяют их отрезками прямых. Полученную фигуру называют многоугольником распределения.

Пример: Дискретная случайная величина X задана законом распределения:
X 1 3 6 8
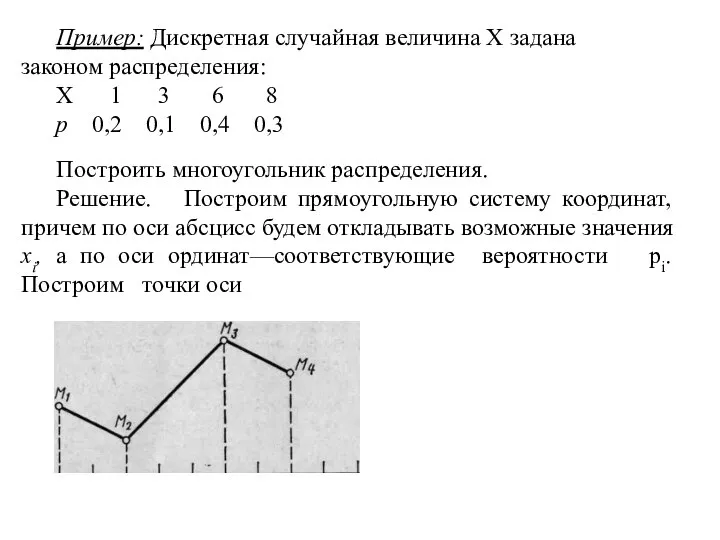
р 0,2 0,1 0,4 0,3
Построить многоугольник распределения.
Решение. Построим прямоугольную систему координат, причем по оси абсцисс будем откладывать возможные значения хi, а по оси ординат—соответствующие вероятности рi. Построим точки оси

Числовые характеристики дискретных случайных величин.
Опр. Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности: М(X) = х1р1 + х2р2 + . . . + хnрп.
Математическое ожидание обладает следующими свойствами.
Свойство 1. Математическое ожидание постоянной величины равно самой постоянной: М(С) = С.
Свойство 2. Постоянный множитель можно выносить за знак математического ожидания: М(СХ) = СМ(Х).
Свойство 3. Математическое ожидание произведения взаимно независимых случайных величин равно произведению математических ожиданий сомножителей:
М (Х1Х2…Хп) = М (Х1) М (Х2)…М(Хп).
Свойство 4. Математическое ожидание суммы случайных величин равно сумме математических ожиданий слагаемых:
М(Х1 + Х2+... +Хn) = М(Х1)+М(Хг) +... +М(Хn).

Опр. Дисперсией случайной величины X называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
Дисперсию удобно вычислять по формуле
D(Х) = М(Х2) — [М(Х)]2.
Дисперсия обладает следующими свойствами.
Свойство 1. Дисперсия постоянной равна нулю:
D(C)=0
Свойство 2. Постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат:
D (CХ) = С2D (X).
Свойство 3. Дисперсия суммы независимых случайных величин равна сумме дисперсий слагаемых:
D(Х1 + Х2+... +Хn) = D(Х1)+D(Хг) +... +D(Хn).

Пример. Найти математическое ожидание дискретной случайной величины X, заданной законом распределения:
а) X - 4 6 10 б) X 0,21 0,54 0,61 Д/з
р 0,2 0,3 0,5 р 0,1 0,5 0,4
Решение. а) Математическое ожидание равно сумме произведений всех возможных значений X на их вероятности:
М(Х) = — 4-0,2 + 6-0,3+10-0,5 = 6.
Пример. Найти математическое ожидание случайной величины Z, если известны математические ожидания X и Y:
а) Z = Х + 2Y, М(Х) = 5, М (Y) = 3;
Решение. а) Используя свойства математического ожидания (математическое ожидание суммы равно сумме математических ожиданий слагаемых; постоянный множитель можно вынести за знак математического ожидания), получим
М (Z) = М (X + 2У) = М (X) + М (2Y) = М (X) + 2М (Y) = 5 + 2*3 = 11.
Пример. Случайны величины X и Y независимы. Найти дисперсию случайной величины Z=3X+2Y, если известно, что D(X)=5, D(Y)=6.
D(Z)=D(3X+2Y)=D(3X)+D(2Y)=9D(X)+4D(Y)=9*5+4*6=69

2. Закон больших чисел
Закон больших чисел - это среднее арифметическое какой-либо большой выборки из фиксированного распределения близко к математическому ожиданию этого распределения.
Понятия закона больших чисел и его трактовка
Говоря более простым языком, то в законе больших чисел количественные закономерности массовых явлений будут явно проявляться только при большом их числе (поэтому и называется закон законом больших чисел).
Отсюда можно сделать вывод, что сущность закона состоит в том, что в числах, которые получаются при массовом наблюдении, имеются некоторые правильности, обнаружить которые в небольшом количестве фактов невозможно.
Сущность закона больших чисел и его примеры
Закон больших чисел выражает наиболее общие закономерности случайного и необходимого. Когда случайные отклонения «гасят» друг друга, средние показатели, определенные для одной и той же структуры, приобретают форму типичных. Они отражают действия существенных и постоянных фактов в конкретных условиях времени и места.

Давайте вспомним обычное бросание монетки. Теоретически орел и решка могут выпасть с одной и той же вероятностью. Это означает, что если, к примеру, бросить монетку 10 раз, 5 из них должна выпасть решка и 5 – орел. Но каждый знает, что так не происходит практически никогда, ведь соотношение частоты выпадения орла и решки может быть и 4 к 6, и 9 к 1, и 2 к 8 и т.д. Однако с увеличением количества подбрасываний монетки, например, до 100, вероятность того, что выпадет орел или решка, достигает 50%. Если же теоретически проводить бесконечное количество подобных опытов, вероятность выпадения монетки обеими сторонами всегда будет стремиться к 50%.
На то, как именно упадет монетка, влияет огромное число случайных факторов. Это и положение монетки на ладони, и сила, с которой совершается бросок, и высота падения, и его скорость и т.д. Но если опытов много, вне зависимости от того, как воздействуют факторы, всегда можно утверждать, что практическая вероятность близка к вероятности теоретической.
А вот еще один пример, который поможет понять сущность закона больших чисел: предположим, что нам нужно оценить уровень заработка людей в каком-то регионе. Если мы будем рассматривать 10 наблюдений, где 9 человек получают 20 тыс. рублей, а 1 человек – 500 тыс. рублей, среднее арифметическое составит 68 тыс. рублей, что, естественно, маловероятно. Но если мы возьмем в расчет 100 наблюдений, где 99 человек получают 20 тыс. рублей, а 1 человек – 500 тыс. рублей, то при расчете среднего арифметического получим 24,8 тыс. рублей, что уже ближе к реальному положению дел. Увеличивая число наблюдений, мы будем заставлять среднее значение стремиться к истинному показателю.