Содержание
- 2. (7.1) Наилучшая линейная процедура получения оценок параметров уравнения (7.1) и условия, при которых эта процедура дает
- 3. Карл Фридрих Гаусс Время жизни 30.04.1777 - 23.02.1855 Научная сфера – математика, физика, астрономия Андрей Андреевич
- 4. Постановка задачи: Имеем случайную выборку наблюдений за поведением экономического объекта объемом n Выборка наблюдений за переменными
- 5. Сформируем вектора и матрицу коэффициентов на основе системы (7.2) Y – вектор выборочных значений эндогенной переменной
- 6. По данным выборки найти: Ã, Cov(ÃÃ), σu, σ(ỹ(z)) Теорема (Гаусса – Маркова) Если матрица Х неколлинеарна
- 7. Тогда наилучшей линейной процедурой оценки параметров модели (7.1) является: (7.3) которая удовлетворяет методу наименьших квадратов При
- 8. Доказательство Воспользуемся методом наименьших квадратов где (7.4) (7.5) Подставив (7.5) в (7.4) получим (7.6)
- 9. Для получения необходимого условия экстремума дифференцируем (7.6) по вектору параметров Откуда система нормальных уравнений для определения
- 10. Докажем несмещенность оценок (7.3) Несмещенность оценки (7.3) доказана Вычислим ковариационную матрицу оценок (7.3) В результате получено
- 11. Пример 1. Пусть имеем выборку из n наблюдений за случайной величиной Y Найти наилучшие оценки среднего
- 12. Решение 1. Вычисляем (XTX)-1 2. Вычисляем (XTY) 3. Вычисляем оценку параметра а0 4. Находим дисперсию среднего
- 13. Пример 2. Уравнение парной регрессии Построить модель типа Y=a0+a1x +u, по данным вы-борки наблюдений за переменными
- 14. 2. Вычисляем XTY 3. Вычисляем оценку вектора параметров а
- 15. Вычислим дисперсии (ковариационную матрицу) параметров модели Следовательно:
- 16. Расчет дисперсии прогнозирования Прогноз осуществляется в точке Z={1,z}Т
- 17. Процедура «ЛИНЕЙН» в приложении EXCEL Алгоритм использования процедуры: Подготовка таблицы исходных данных 2. Вызов процедуры «ЛИНЕЙН»
- 19. Скачать презентацию
















 Деление обыкновенных дробей
Деление обыкновенных дробей Интегрированный урок математики и краеведения. Путешествие по Кизильскому району. Часть 3
Интегрированный урок математики и краеведения. Путешествие по Кизильскому району. Часть 3 Касательная к окружности. 8 класс
Касательная к окружности. 8 класс Путь и перемещение
Путь и перемещение Презентация на тему Умножение десятичных дробей на натуральные числа
Презентация на тему Умножение десятичных дробей на натуральные числа  Деление суммы на число
Деление суммы на число Обобщение. Высказывания. Ориентирование на местности
Обобщение. Высказывания. Ориентирование на местности Интерактивная игра для детей дошкольного возраста Путешествие в страну Математика
Интерактивная игра для детей дошкольного возраста Путешествие в страну Математика Подготовка к блиц-турниру
Подготовка к блиц-турниру Таблицы умножения и деления на 2 и 3
Таблицы умножения и деления на 2 и 3 Множення десяткових дробів. 5 клас
Множення десяткових дробів. 5 клас Степенная функция и её график
Степенная функция и её график Многогранники. Розв'язування задач
Многогранники. Розв'язування задач Обыкновенные дифференциальные уравнения. Вариант 4
Обыкновенные дифференциальные уравнения. Вариант 4 Решение уравнений (урок 3). 6 класс
Решение уравнений (урок 3). 6 класс Понятия и свойства функции. Предел функции
Понятия и свойства функции. Предел функции Число 0. Цифра 0
Число 0. Цифра 0 Предмет стереометрии. Аксиомы стереометрии
Предмет стереометрии. Аксиомы стереометрии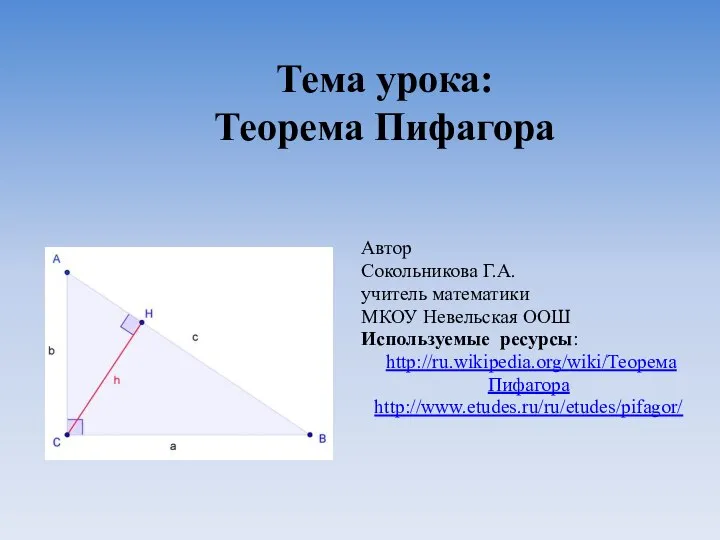 Теорема Пифагора
Теорема Пифагора Презентация на тему Изображение пространственных фигур
Презентация на тему Изображение пространственных фигур 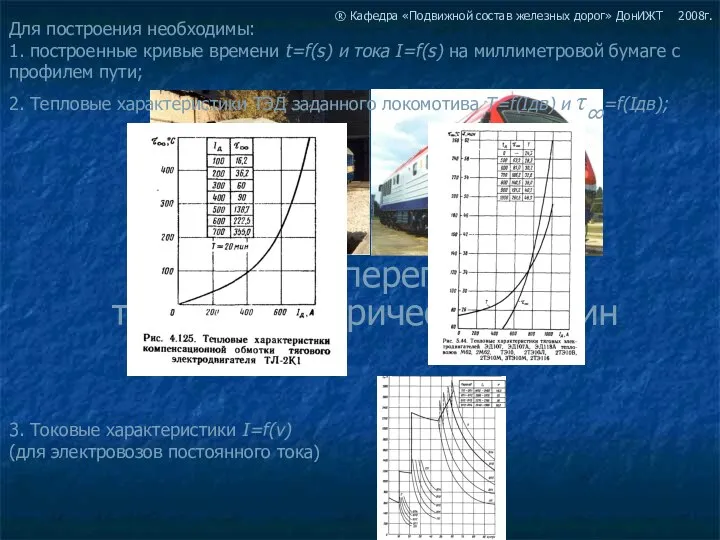 Расчет перегрева тяговых электрических машин
Расчет перегрева тяговых электрических машин Степенные функции, их свойства и графики
Степенные функции, их свойства и графики Введение в фармакологию
Введение в фармакологию Медианы, биссектрисы и высоты треугольника
Медианы, биссектрисы и высоты треугольника Функции и их графики
Функции и их графики Производная произведения. Производная частного
Производная произведения. Производная частного Сечение куба, призмы, пирамиды
Сечение куба, призмы, пирамиды Параллельный перенос и поворот
Параллельный перенос и поворот