Содержание
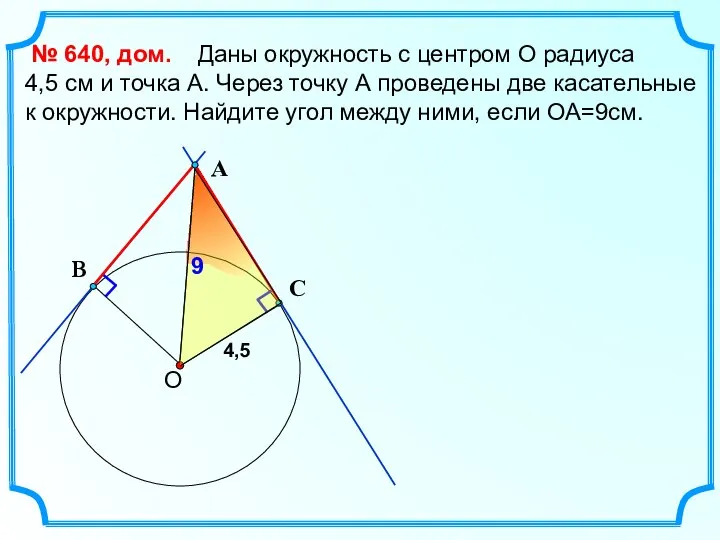
- 2. Даны окружность с центром О радиуса 4,5 см и точка А. Через точку А проведены две
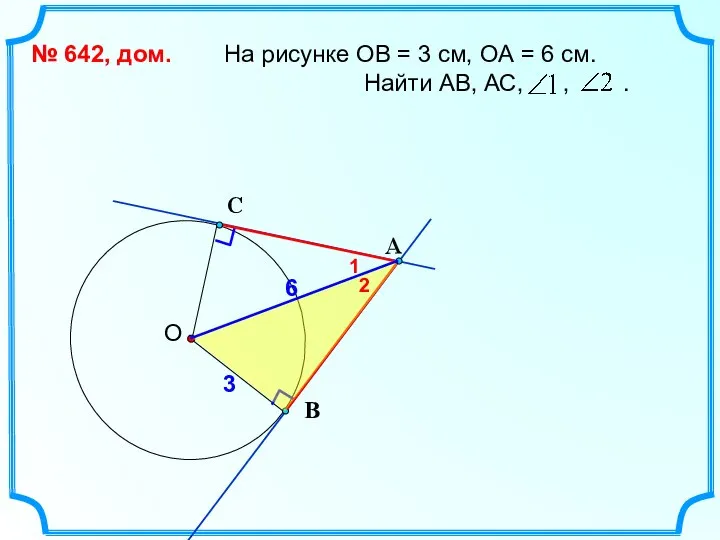
- 3. На рисунке ОВ = 3 см, ОА = 6 см. Найти АВ, АС, , . №
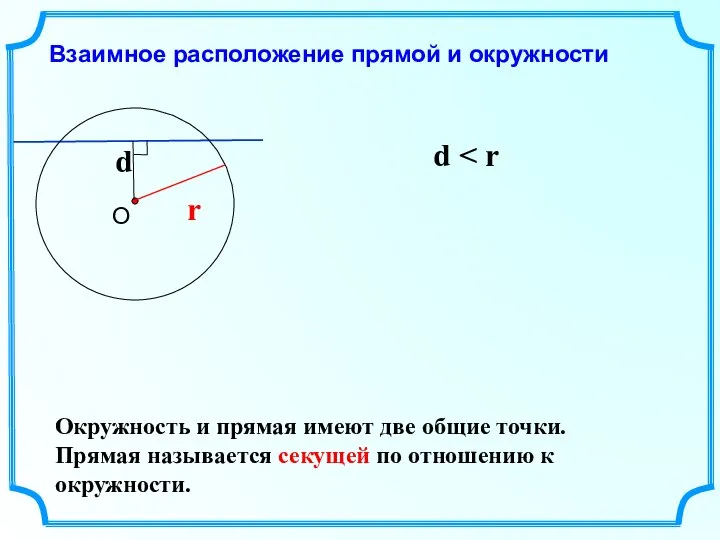
- 4. Взаимное расположение прямой и окружности d r d Окружность и прямая имеют две общие точки. Прямая
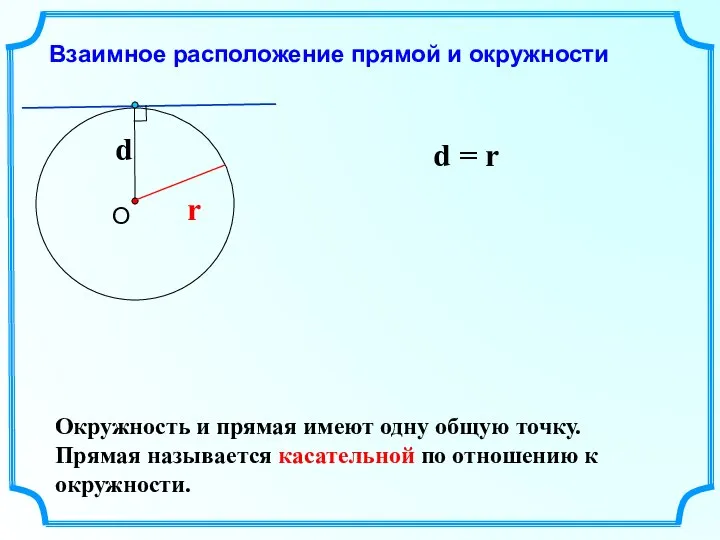
- 5. Взаимное расположение прямой и окружности r d = r Окружность и прямая имеют одну общую точку.
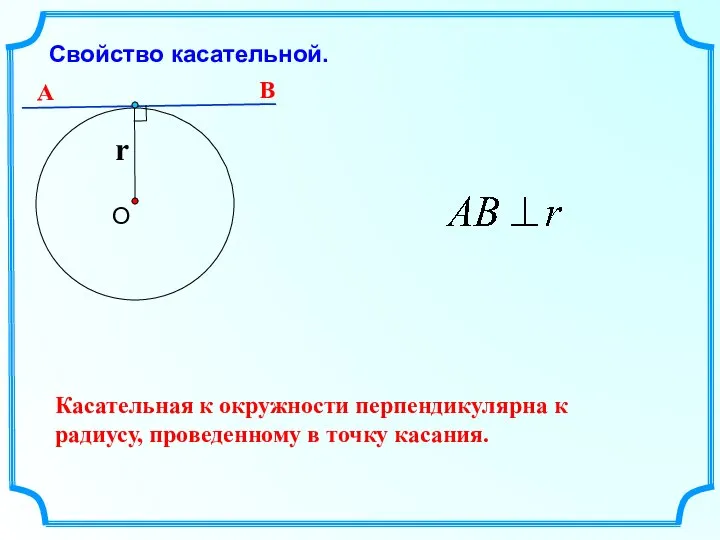
- 6. Свойство касательной. Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания. А В
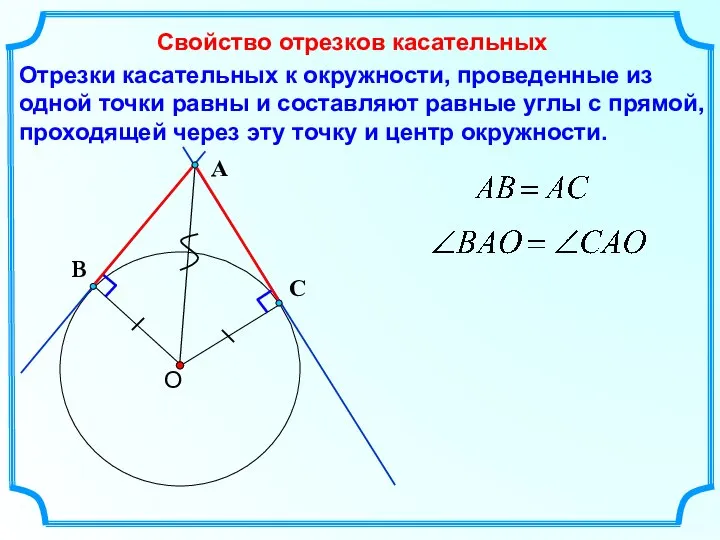
- 7. Отрезки касательных к окружности, проведенные из одной точки равны и составляют равные углы с прямой, проходящей
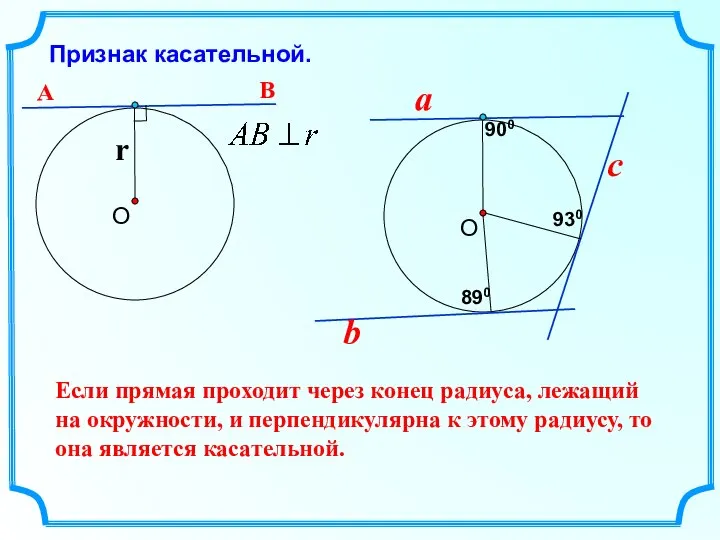
- 8. Признак касательной. О r Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна к
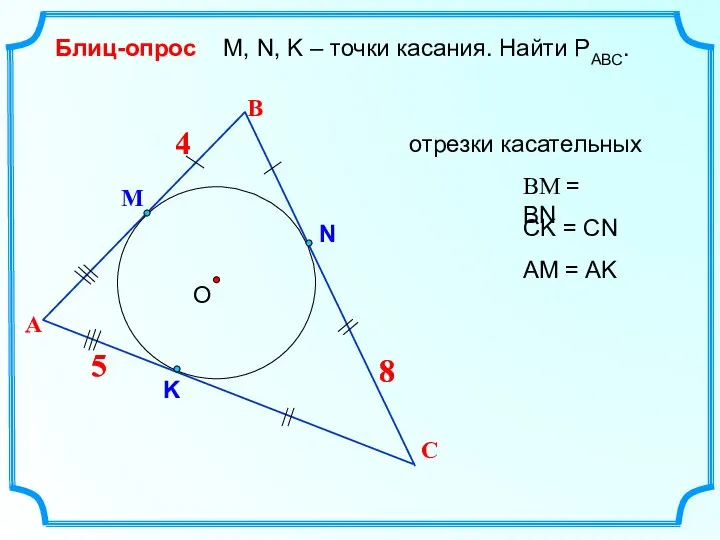
- 9. 4 В О М, N, K – точки касания. Найти РАВС. Блиц-опрос А 4 С М
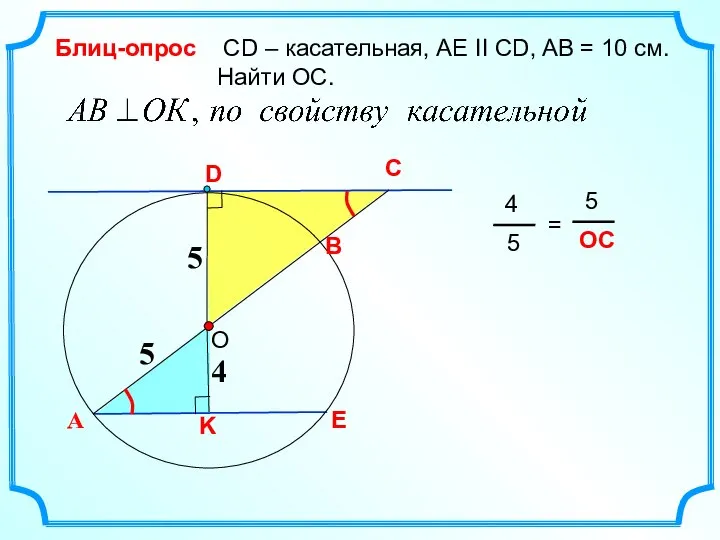
- 10. C СD – касательная, AE II CD, AB = 10 см. Найти ОС. Блиц-опрос 4 А
- 11. 8 класс Л.С. Атанасян Геометрия 7-9 Центральные и вписанные углы
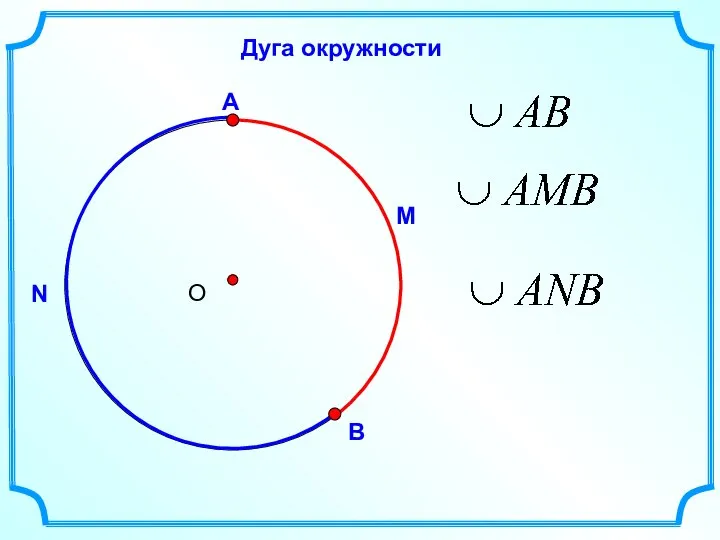
- 12. Дуга окружности М
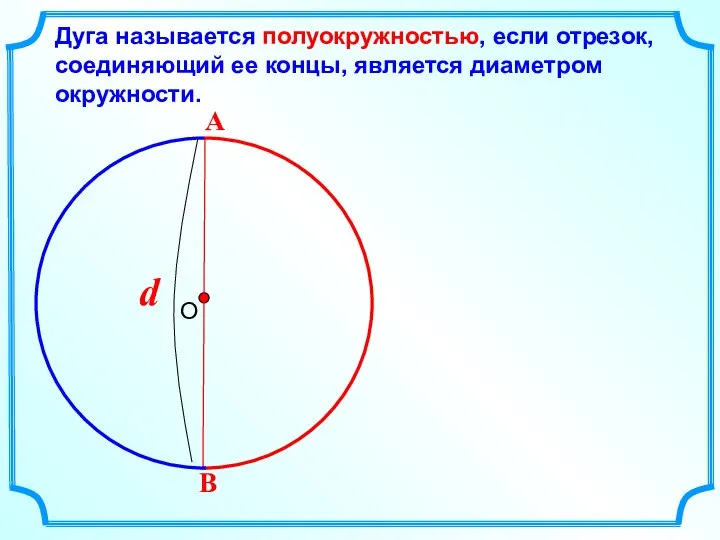
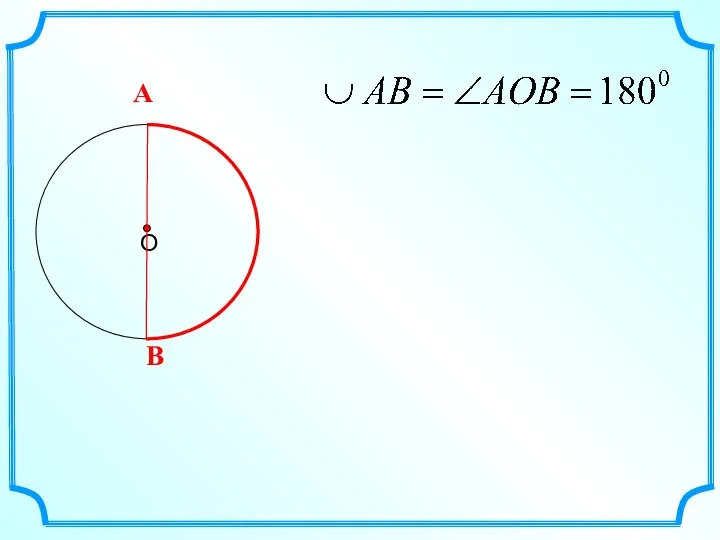
- 13. Дуга называется полуокружностью, если отрезок, соединяющий ее концы, является диаметром окружности.
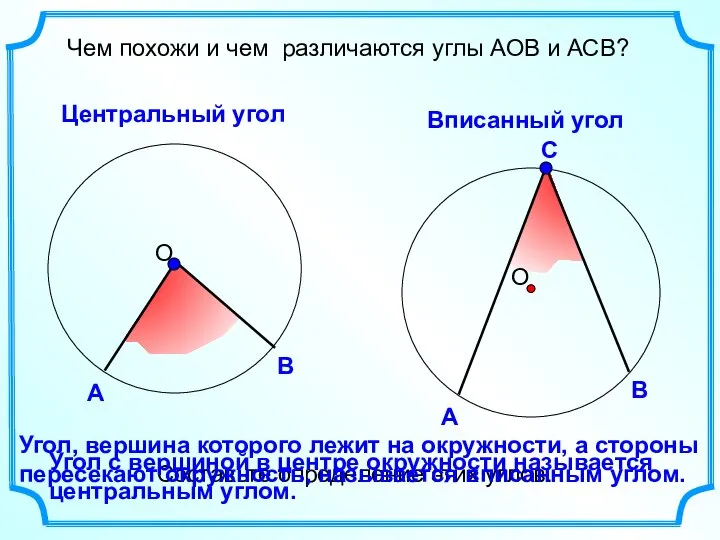
- 14. Чем похожи и чем различаются углы АОВ и АСВ? Центральный угол Вписанный угол Составьте определение этих
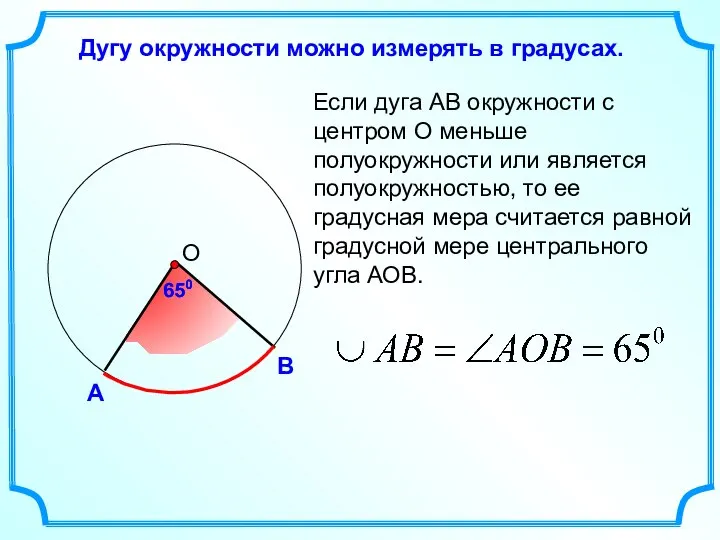
- 15. Дугу окружности можно измерять в градусах. Если дуга АВ окружности с центром О меньше полуокружности или
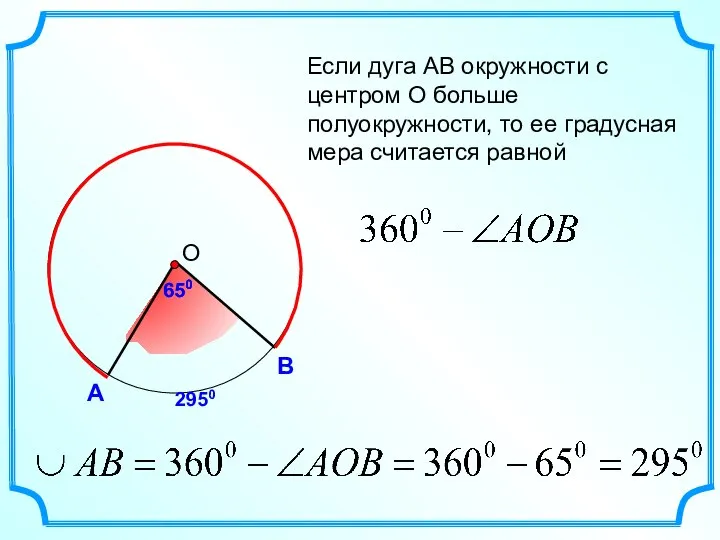
- 17. А В Если дуга АВ окружности с центром О больше полуокружности, то ее градусная мера считается
- 19. Скачать презентацию

 Дизъюнктивные нормальные формы (ДНФ). СДНФ
Дизъюнктивные нормальные формы (ДНФ). СДНФ Определители. Обратная матрица. Ранг матрицы
Определители. Обратная матрица. Ранг матрицы Проценты в медицине
Проценты в медицине Основы геометрии
Основы геометрии Применение производной к исследованию функции
Применение производной к исследованию функции Симметрии. Осевая симметрия
Симметрии. Осевая симметрия Линейная функция, ее график и свойства (занятие 2)
Линейная функция, ее график и свойства (занятие 2) Сумма углов треугольника
Сумма углов треугольника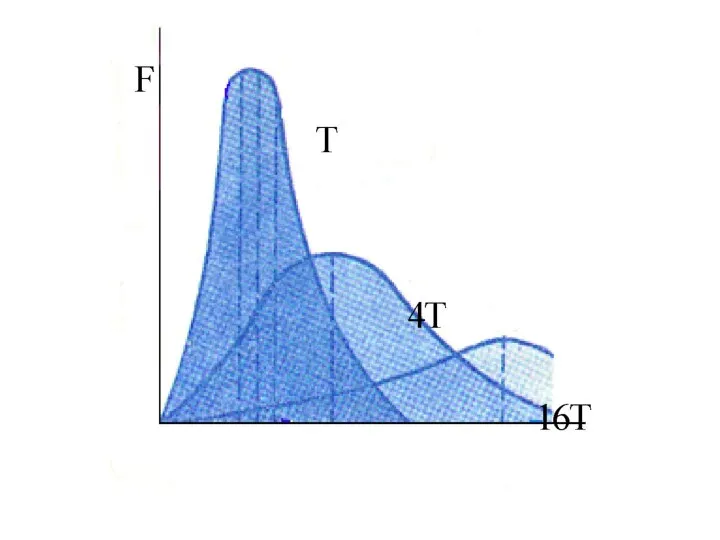 Функция распределения Максвелла
Функция распределения Максвелла Двугранный угол. Перпендикулярность плоскостей
Двугранный угол. Перпендикулярность плоскостей Окружность. Методическая разработка урока
Окружность. Методическая разработка урока Построение сечений
Построение сечений Задачи математической карусели. 4 класс
Задачи математической карусели. 4 класс Вычисление площадей с помощью интегралов
Вычисление площадей с помощью интегралов Математическая психология
Математическая психология Основы планирования режимов технической эксплуатации (техническое обслуживание и его характеристика)
Основы планирования режимов технической эксплуатации (техническое обслуживание и его характеристика) Многоугольники
Многоугольники Игра Жизнь Conway's Game of Life
Игра Жизнь Conway's Game of Life Знаки неравенств. Историческая справка
Знаки неравенств. Историческая справка Натуральный логарифм. Функция y=ln x, её свойства, график, дифференцирование
Натуральный логарифм. Функция y=ln x, её свойства, график, дифференцирование Тренажер. Таблица умножения пяти. Анимированная сорбонка
Тренажер. Таблица умножения пяти. Анимированная сорбонка Умножение и деление на однозначное число
Умножение и деление на однозначное число Масштаб и его виды
Масштаб и его виды Четырехугольники
Четырехугольники Вводный урок. Теоретический материал
Вводный урок. Теоретический материал Презентация на тему ИЗМЕРЕНИЕ ОТРЕЗКОВ
Презентация на тему ИЗМЕРЕНИЕ ОТРЕЗКОВ  ریاضی جزوه کامل
ریاضی جزوه کامل Решение тригонометрических уравнений
Решение тригонометрических уравнений