Тетраэдр и параллелепипед

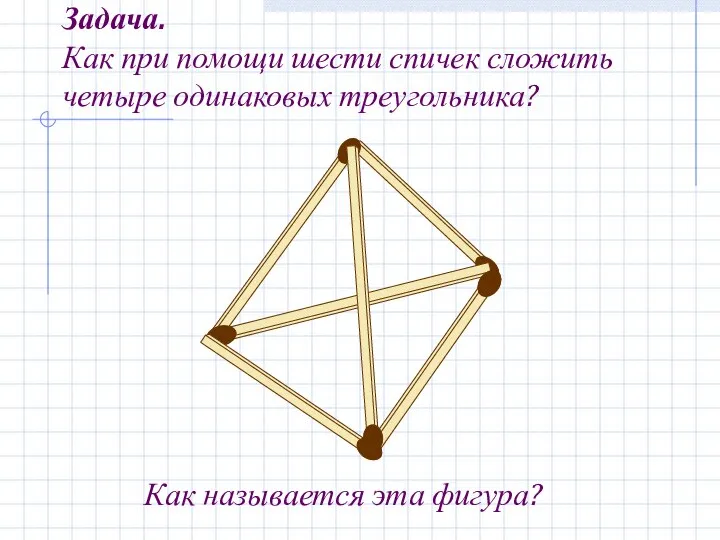
Задача.
Как при помощи шести спичек сложить
четыре одинаковых треугольника?
Как называется эта фигура?

Тетраэдр

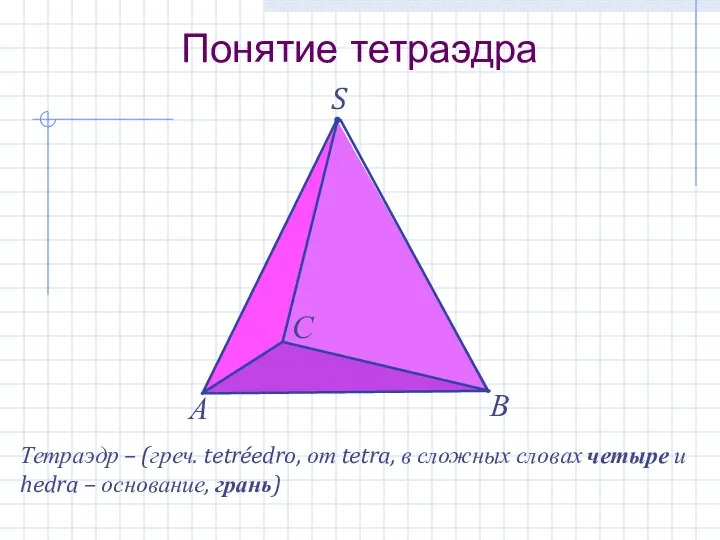
S
Понятие тетраэдра
А
В
С
Тетраэдр – (греч. tetréedro, от tetra, в сложных словах четыре и hedra – основание, грань)

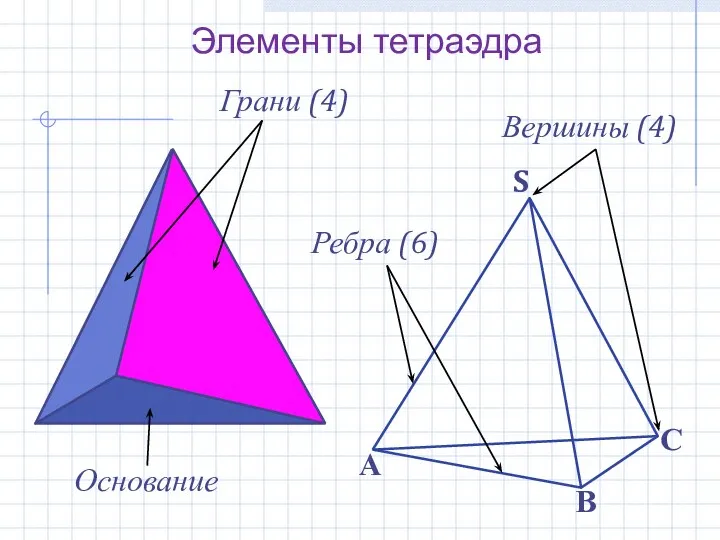
Элементы тетраэдра
Грани (4)
Ребра (6)
Вершины (4)
Основание

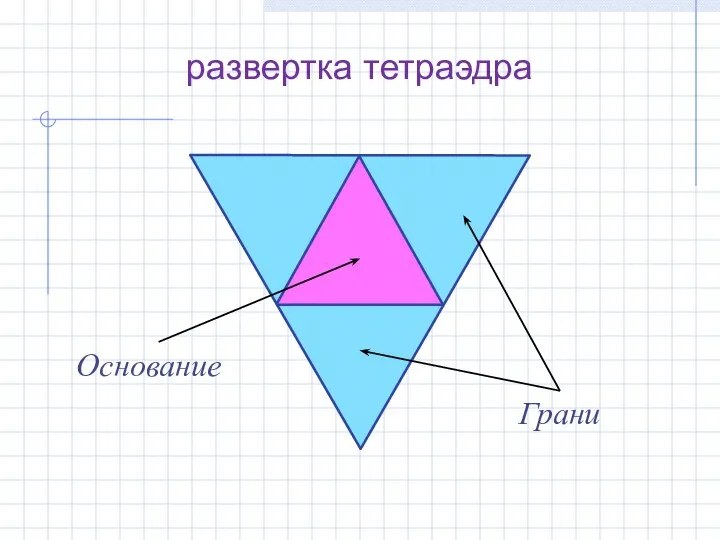
развертка тетраэдра
Грани
Основание

Гигантский тетраэдр для Нового Орлеана
Разработанное для Нового Орлеана «здание-город» NOAH (New Orleans Arcology Habitat) возвышается на 365 метров, включает в себя 20000 квартир, суммарная жилая площадь которых равна 2 040 000 кв.м. Здание использует экологичное энергоснабжение – энергию ветра, воды и солнца. Кроме квартир в тетраэдре помещаются коммерческие организации, три отеля, культурные объекты, школа, больницы и казино. И, учитывая место, под которое создавался проект, его немаловажная особенность — способность держаться на плаву.

Настенный тетраэдр
Аппарат Delto
Аппарату предназначено взбираться по вертикальным поверхностям — например, по стенам многоэтажных зданий. Только по специально подготовленному — с размещёнными в нужных местах креплениями типа альпинистских. Именно за них цепляется Delto своими вершинами, вперевалку перебираясь всё выше и выше.

Задача 2
А можно ли из развертки тетраэдра сделать многогранник большего объема, чем сам тетраэдр?

параллелепипед

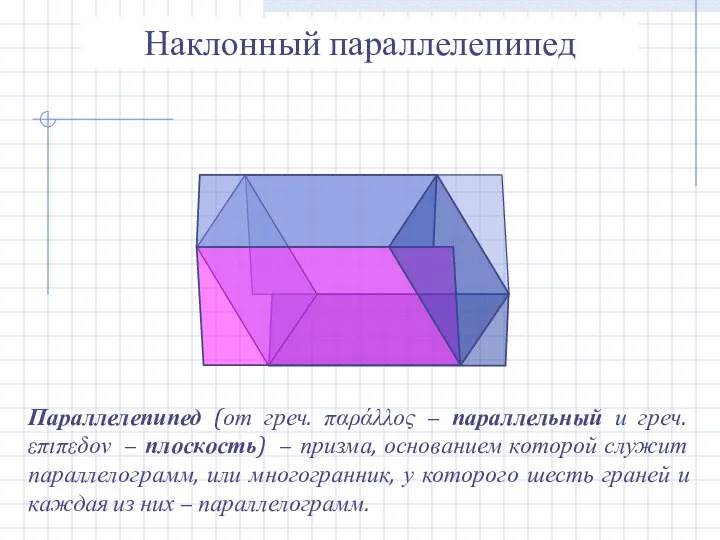
Наклонный параллелепипед
Параллелепипед (от греч. παράλλος − параллельный и греч. επιπεδον − плоскость) − призма, основанием которой служит параллелограмм, или многогранник, у которого шесть граней и каждая из них − параллелограмм.

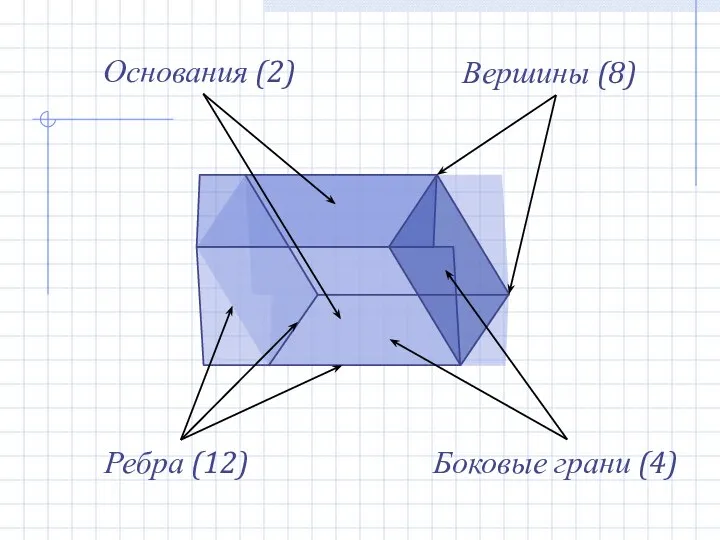
Ребра (12)
Боковые грани (4)
Вершины (8)
Основания (2)

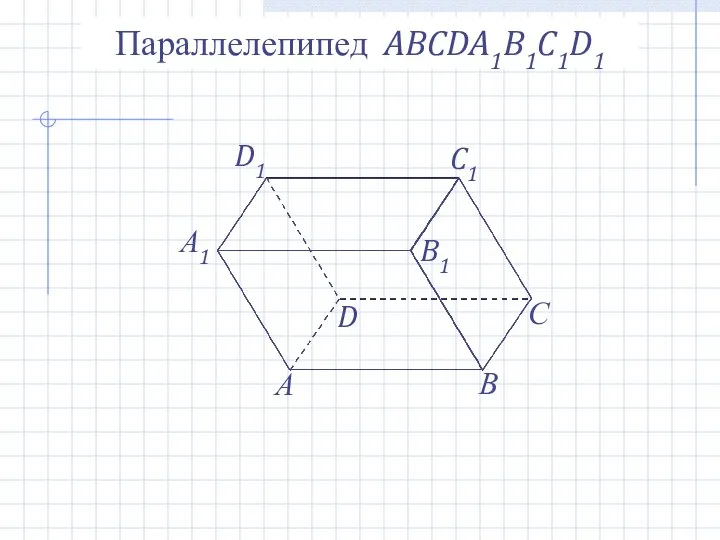
Параллелепипед ABCDA1B1C1D1

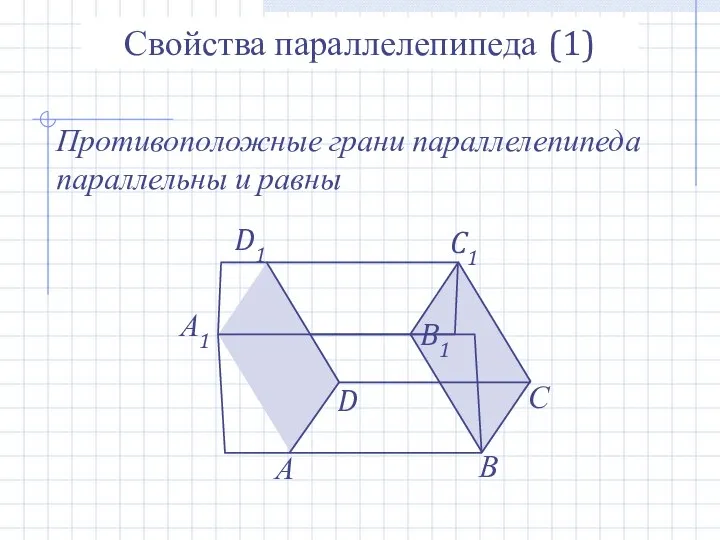
А
В
С
А1
D
D1
B1
C1
Свойства параллелепипеда (1)
Противоположные грани параллелепипеда параллельны и равны

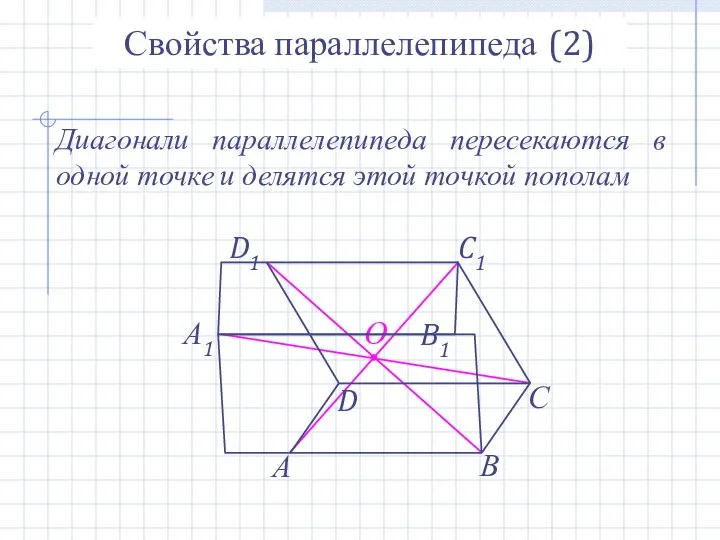
О
Свойства параллелепипеда (2)
Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам

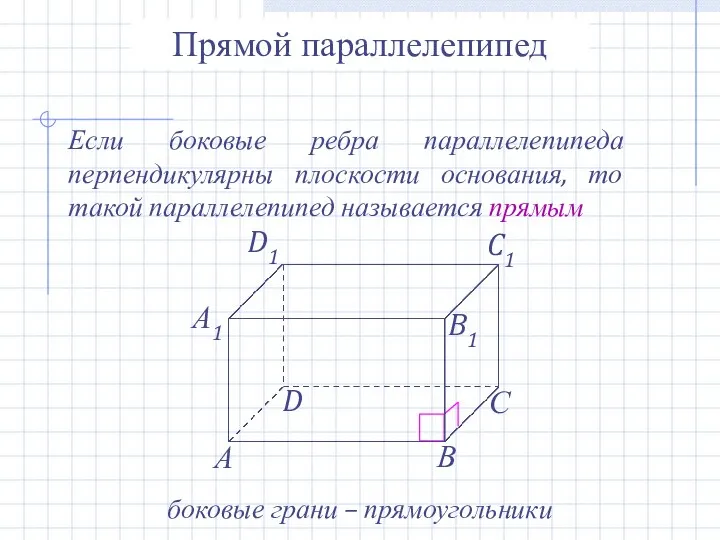
Прямой параллелепипед
Если боковые ребра параллелепипеда перпендикулярны плоскости основания, то такой параллелепипед называется прямым
боковые грани – прямоугольники

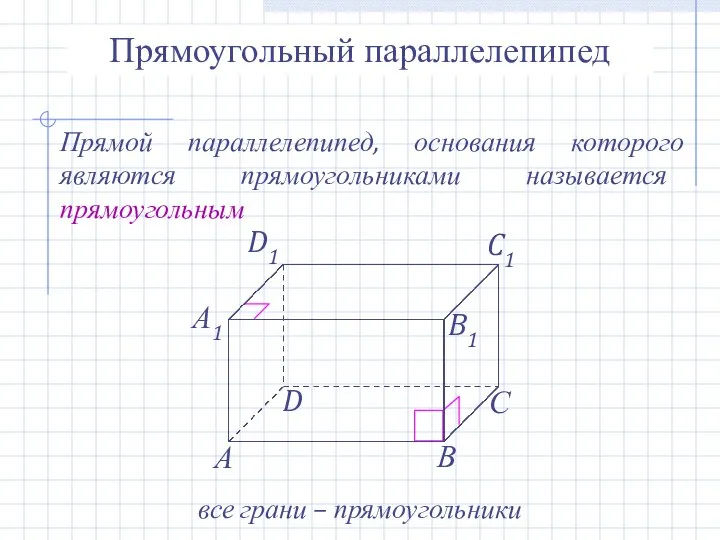
Прямоугольный параллелепипед
Прямой параллелепипед, основания которого являются прямоугольниками называется прямоугольным
все грани – прямоугольники

Свойства прямоугольного параллелепипеда
1° В прямоугольном параллелепипеде все шесть граней – прямоугольники
2° Все двугранные углы прямоугольного параллелепипеда– прямые

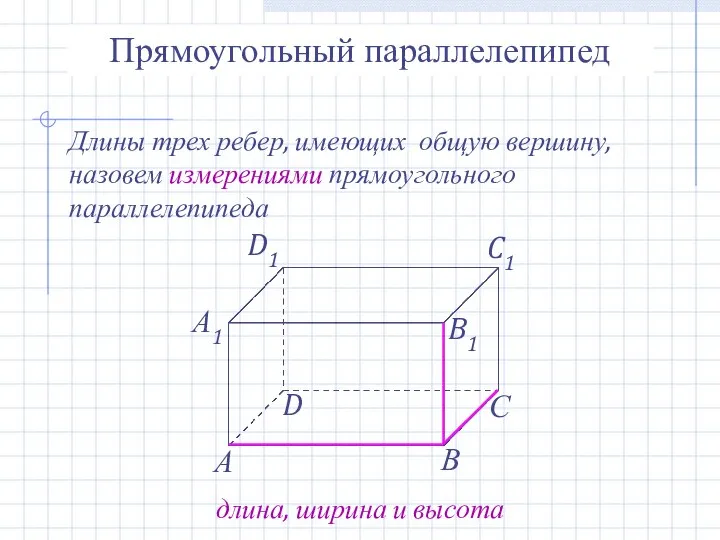
Прямоугольный параллелепипед
Длины трех ребер, имеющих общую вершину, назовем измерениями прямоугольного параллелепипеда
длина, ширина и высота

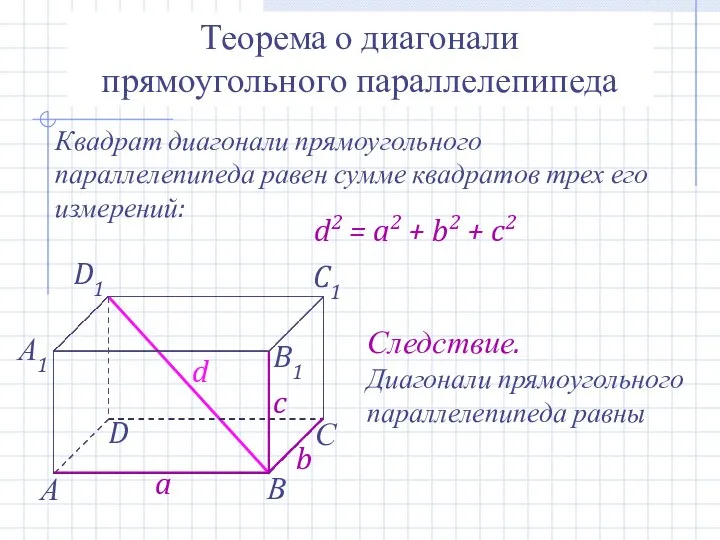
Теорема о диагонали прямоугольного параллелепипеда
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений:
d2 = a2 + b2 + c2
a
b
c
d
Следствие.
Диагонали прямоугольного параллелепипеда равны

Куб
Прямоугольный параллелепипед, все грани которого – равные квадраты называется кубом
все грани – равные квадраты
d2 = 3a2
d
a
a
a

Примеры использования формы параллелепипеда