Содержание
- 2. План урока: 1. Понятие цилиндра 2. Прямой круговой цилиндр и его элементы 3. Сечение цилиндра плоскостью
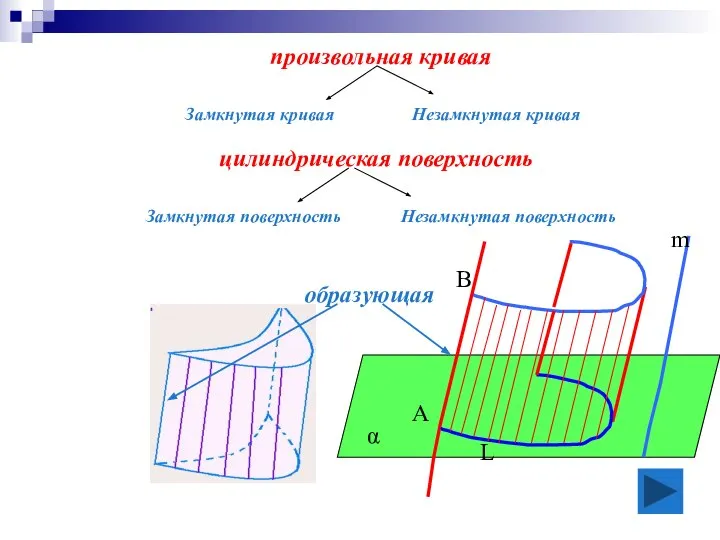
- 3. образующая цилиндрическая поверхность произвольная кривая Незамкнутая поверхность Замкнутая кривая Незамкнутая кривая Замкнутая поверхность А m α
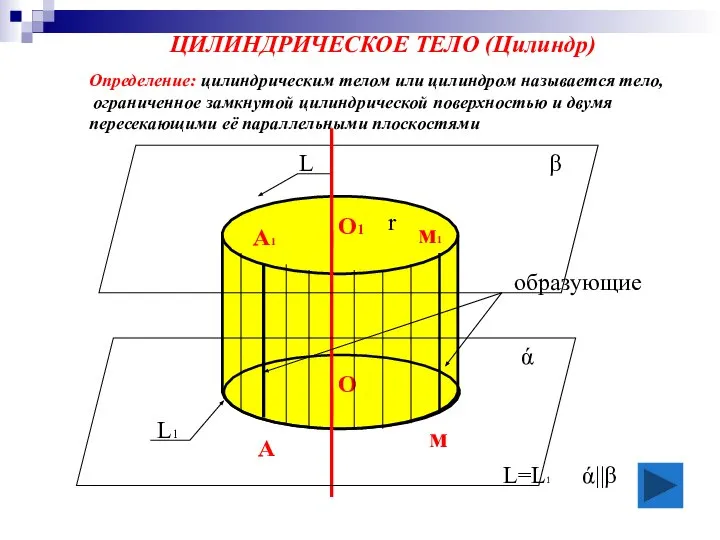
- 4. ЦИЛИНДРИЧЕСКОЕ ТЕЛО (Цилиндр) образующие О1 О ά β м1 м r ά||β L L1 L=L1 А
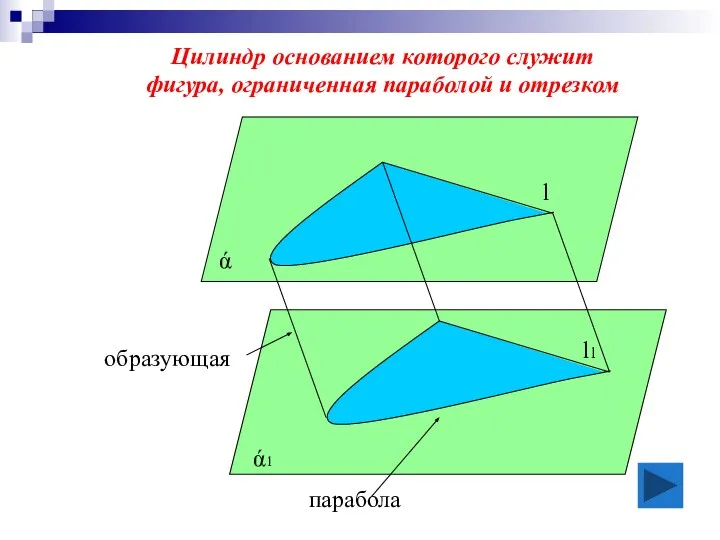
- 5. Цилиндр основанием которого служит фигура, ограниченная параболой и отрезком l l1 образующая ά ά1 парабола
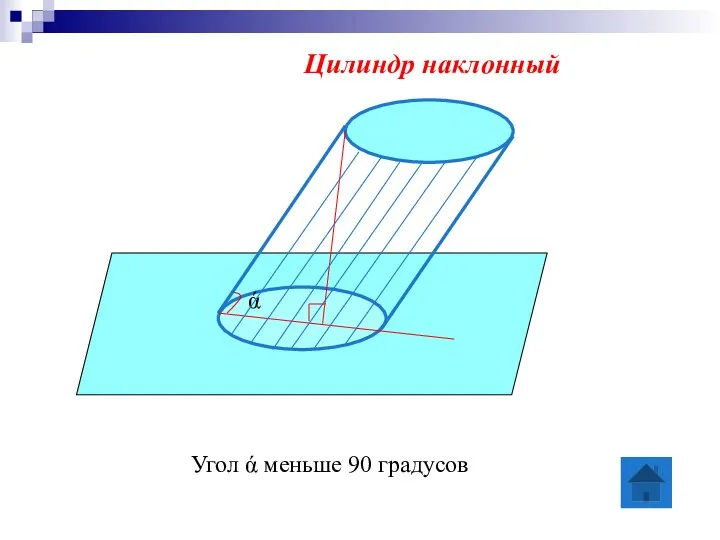
- 6. Угол ά меньше 90 градусов Цилиндр наклонный
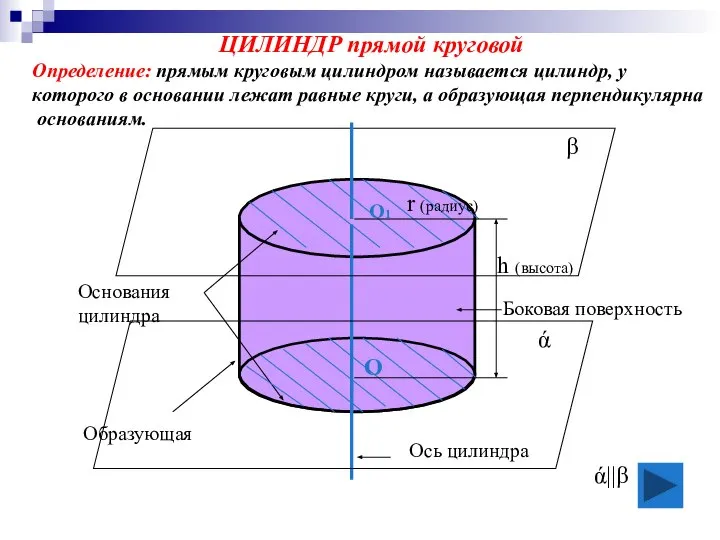
- 7. ЦИЛИНДР прямой круговой Определение: прямым круговым цилиндром называется цилиндр, у которого в основании лежат равные круги,
- 8. 3. Радиусом цилиндра называется радиус его основания. 4. Высота цилиндра- расстояние между плоскостями оснований, в прямом
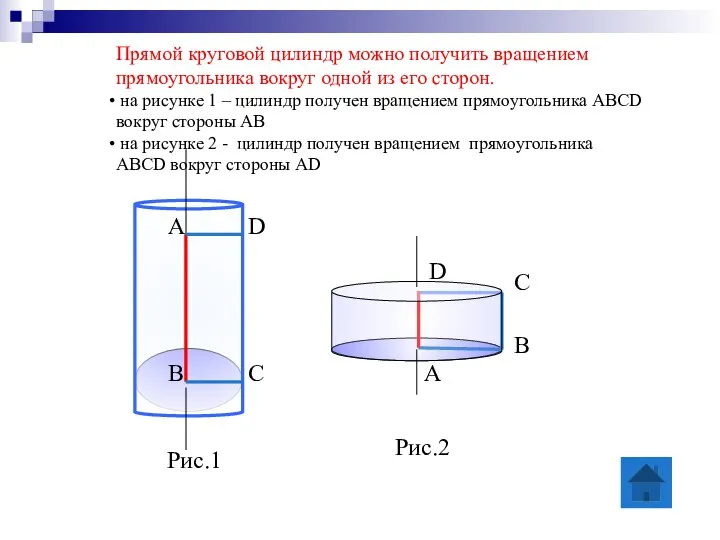
- 9. А D В С Рис.1 Прямой круговой цилиндр можно получить вращением прямоугольника вокруг одной из его
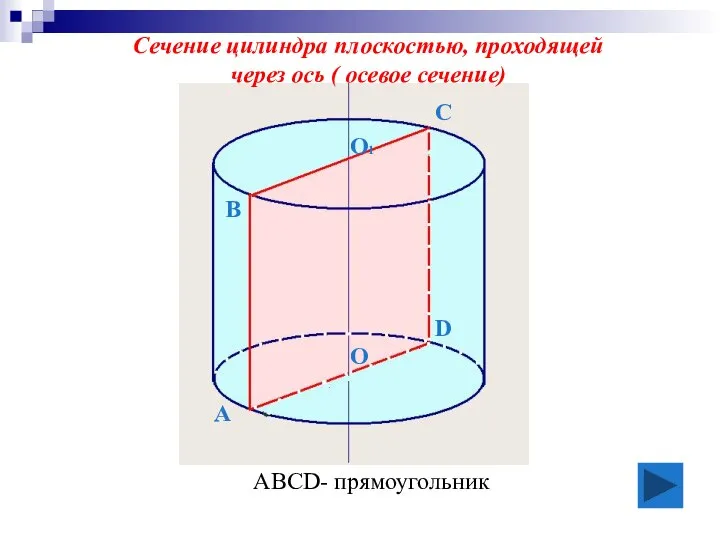
- 10. А В С D О О1 Сечение цилиндра плоскостью, проходящей через ось ( осевое сечение) АВСD-
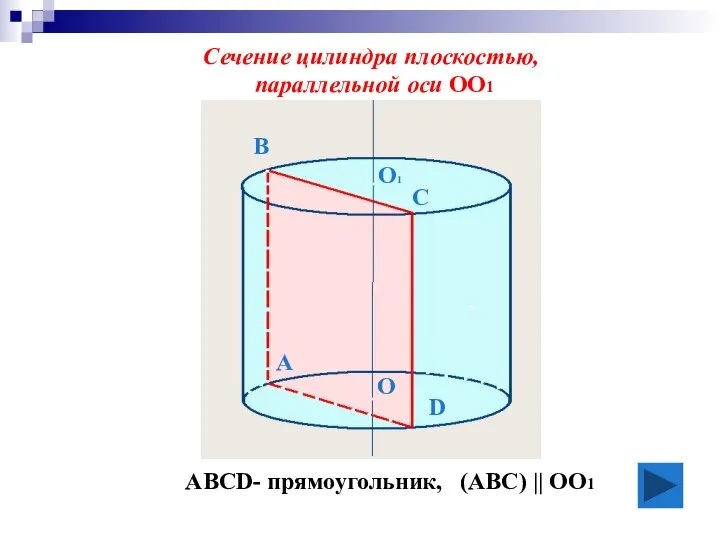
- 11. А В С D АВСD- прямоугольник, (ABC) || ОО1 О1 Сечение цилиндра плоскостью, параллельной оси ОО1
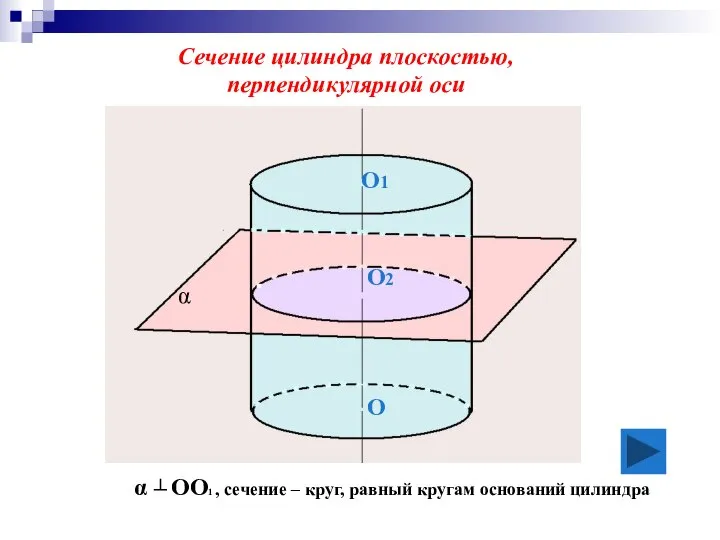
- 12. α ┴ OO1 , сечение – круг, равный кругам оснований цилиндра Сечение цилиндра плоскостью, перпендикулярной оси
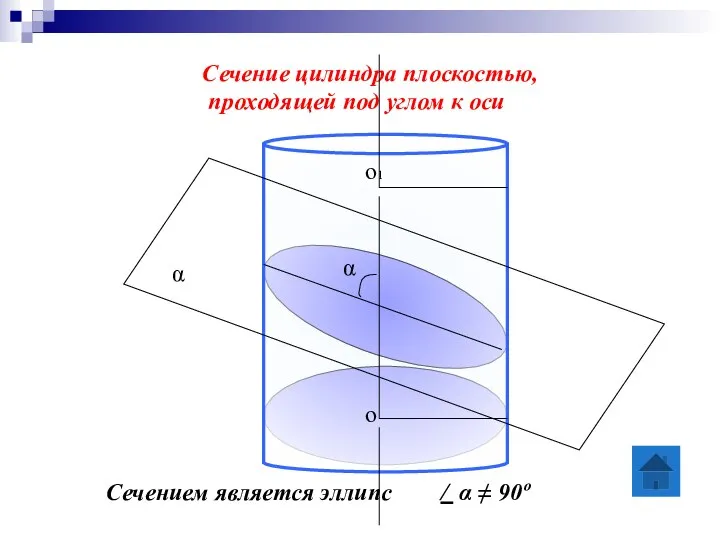
- 13. Сечение цилиндра плоскостью, проходящей под углом к оси Сечением является эллипс α / α ≠ 90º
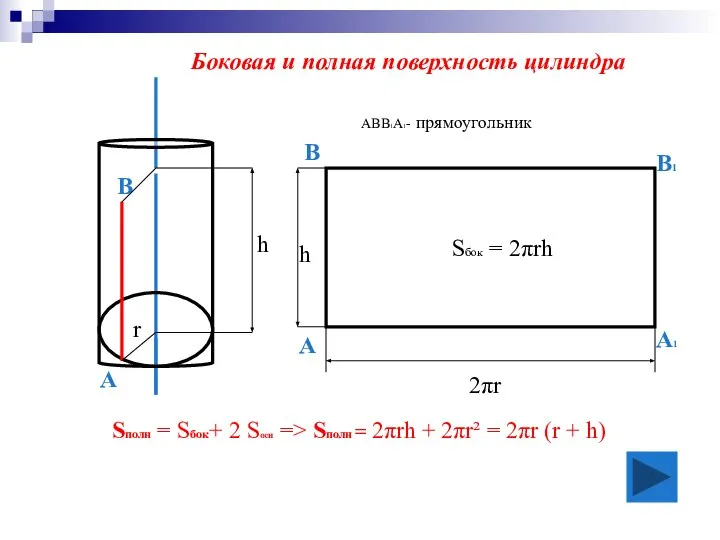
- 14. АВВ1А1- прямоугольник В А1 В1 А 2πr h Sбок = 2πrh Sполн = Sбок+ 2 Sосн
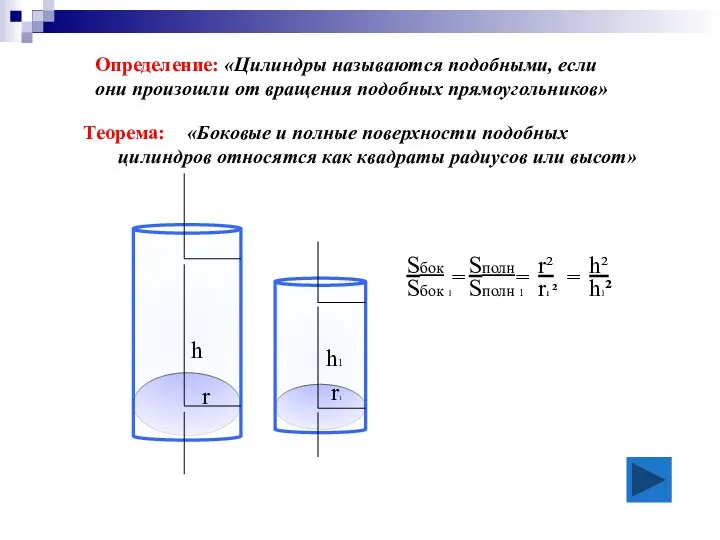
- 15. «Боковые и полные поверхности подобных цилиндров относятся как квадраты радиусов или высот» Теорема: Определение: «Цилиндры называются
- 16. Внимание!
- 17. Задача Первый вариант Вычислите полную и боковую поверхность цилиндра, радиус которого равен 3 м, а высота
- 18. Историческая справка Слово «цилиндр» происходит от греческого слова «ΚΙΛΙΝΔΡΟΣ», что означает «валик», «каток».
- 39. Ответь на вопросы 1. Назови элементы цилиндра 2.Назови вид осевого сечения цилиндра 3. Может ли сечение
- 41. Скачать презентацию


























 Прикладна математика
Прикладна математика Решение задач на разностное сравнение 2 класс - Презентация
Решение задач на разностное сравнение 2 класс - Презентация Геометрическая мозаика из правильных одноимённых многоугольников
Геометрическая мозаика из правильных одноимённых многоугольников Домашнее задание по математике
Домашнее задание по математике Таблица умножения числа 2 и на 2
Таблица умножения числа 2 и на 2 Презентация на тему Пределы. Непрерывность функций
Презентация на тему Пределы. Непрерывность функций 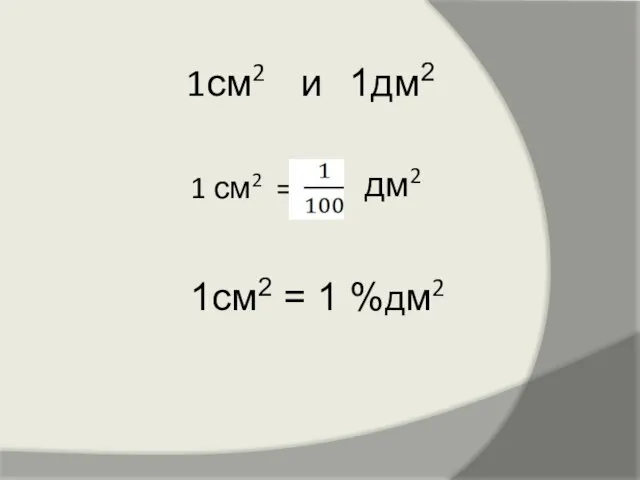 Презентация по математике "Проценты. Сотая часть Вселенной" -
Презентация по математике "Проценты. Сотая часть Вселенной" -  Представляют геометрические фигуры
Представляют геометрические фигуры Практическое занятие Числа
Практическое занятие Числа Тригонометрическая и показательная форма комплексного числа
Тригонометрическая и показательная форма комплексного числа Доли. Часы
Доли. Часы Коэффициент корреляции
Коэффициент корреляции Геометрия. Билет 10
Геометрия. Билет 10 Методология и методы в статистике
Методология и методы в статистике Презентация по математике "Сложение и вычитание в пределах 1000" -
Презентация по математике "Сложение и вычитание в пределах 1000" -  Основы теории графов
Основы теории графов The most attractive mathematical formulas
The most attractive mathematical formulas Объёмные тела в повседневной жизни
Объёмные тела в повседневной жизни Решение задач по теме Параллельность прямой и плоскости
Решение задач по теме Параллельность прямой и плоскости Презентация на тему Решение задач В ЕГЭ по теории вероятности
Презентация на тему Решение задач В ЕГЭ по теории вероятности  Comparative of superlative
Comparative of superlative Аксиомы стереометрии и их следствия
Аксиомы стереометрии и их следствия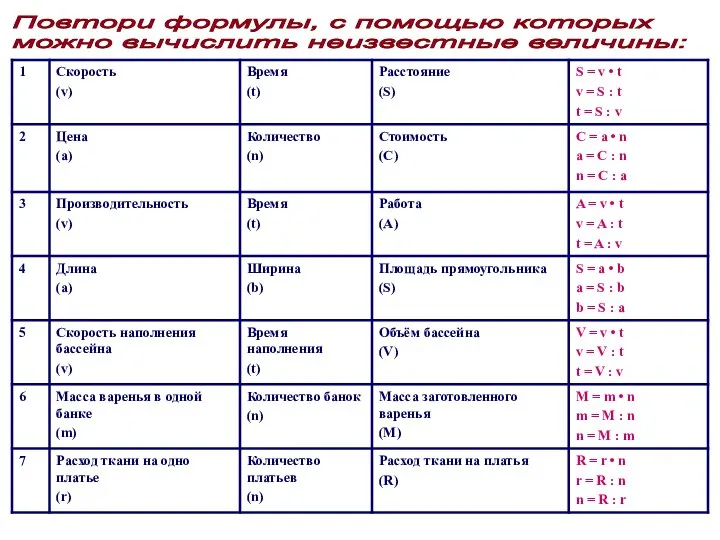 Скорость (v), Время (t), Расстояние (S)
Скорость (v), Время (t), Расстояние (S) Сложение и вычитание многозначных чисел. Игра Чей шарик?
Сложение и вычитание многозначных чисел. Игра Чей шарик? Интерактивный тренажёр В стране Математики. 1 класс
Интерактивный тренажёр В стране Математики. 1 класс Параллельность и перпендикулярность прямых и плоскостей в пространстве
Параллельность и перпендикулярность прямых и плоскостей в пространстве Приемы устных вычислений в пределах 100. 3 класс
Приемы устных вычислений в пределах 100. 3 класс Треугольник
Треугольник